LMA上课笔记

一门课的笔记，自用。整理出来当做给自己留个纪念

---

数学公式或相关推导

协方差矩阵一定是半正定的
已知$\underline{x}$和它的期望$\underline{\mu }$，则的协方差矩阵为$E[(\underline{x}-\underline{\mu })(\underline{x}-\underline{\mu }{)}^T]$，对于任意向量$\underline{y}$有：
${\underline{y}}^T\Sigma \underline{y}=E[{\underline{y}}^T(\underline{x}-\underline{\mu })(\underline{x}-\underline{\mu }{)}^T\underline{y}]=E[((\underline{x}-\underline{\mu }{)}^T\underline{y}{)}^T((\underline{x}-\underline{\mu }{)}^T\underline{y})]=E[||(\underline{x}-\underline{\mu }{)}^T\underline{y}|{|}^2]\ge 0$

期望与协方差的基础知识
①如果$\underline{z}=A\underline{x}$，那么就有$E(\underline{z})=A\ast E(\underline{x})，C_z=A\ast C_x\ast A^T$
②如果有$\underline{b}为定量$，那么$E(\underline{x}+\underline{b})=E(\underline{x})+\underline{b}，Cov(\underline{x}+\underline{b})=C_x$
③如果$\underline{y}$不确定而且和$\underline{x}$相互独立，那么$Cov(\underline{x},\underline{y})=E((\underline{x}-E(\underline{x}))(\underline{y}-E(\underline{y})))=0$，并且还满足：
$E(\underline{x}+\underline{y})=E(\underline{x})+E(\underline{y}),Cov(\underline{x}+\underline{y})=C_x+C_y$

随机变量的独立性
两个随机变量$\underline{a}$和$\underline{b}$，如果有$P(\underline{b}|\underline{a})\ne P(\underline{b})$，那么这两个变量就不是相互独立的。
如果$\underline{a}$和$\underline{b}$是互相独立的，那么有$Cov(\underline{a},\underline{b})=0$

$Cov(A\underline{a},B\underline{b})=ACov(\underline{a},\underline{b})B^T$
$Cov(\underline{a}+\underline{b},\underline{c})=Cov(\underline{a},\underline{c})+Cov(\underline{b},\underline{c})$

求点到直线的距离
直线的表达形式为Ax + By + C = 0时，点到直线的距离公式为：

如果直线方程已经经过归一化，那么这条直线的法向量就是(A,B).

矩阵的秩是什么？满秩是什么意思？
the number of linearly independent rows or columns in a matrix
满秩矩阵是判断一个矩阵是否可逆的充分必要条件。

怎么证明矩阵B $\ge$ 矩阵A
B-A是半正定的即可

矩阵求导

大纲内容梳理

一. 综述性内容

• 什么是定位？
  determination of the location of moving object step by step

• 什么是位姿和状态？
  pose: position&orientation (+uncertainty)
  – 2D pose: 朝向可以用一个角度值表示
  – 3D pose: 朝向可以用旋转矩阵，欧拉角，四元数表示
  status: 可以有位置、速度等

• 不确定度的表示方法
  区间表示，概率密度函数，期望和协方差矩阵

• 怎么对一个协方差矩阵（方阵）A（或者说是不确定度）进行可视化：elliptic with Eigendecomposition

  1. 求出它的特征值$e_i$和特征向量$v_i$
  2. 画一个半径为1的圆
  3. 将轴i长度乘以$\sqrt{e_i}$
  4. 把圆形进行旋转，旋转矩阵$R=[v_1,v_2]$（2维的情况）
     

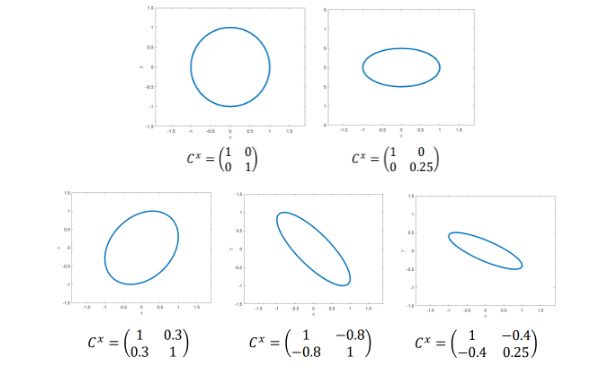
  这个地方，如果换一个角度，可以理解为画出所有的$\underline{x}$，使得有${\underline{x}}^T\ast A\ast \underline{x}=1$。其实就是画出Mahalanobis距离为1的地方。

• 能影响到定位方法的因素： accuracy, latenz, sampling rate, affected range

二. Koppelnavigation

初识

• Koppelnavigation是什么？
  已知物体的初始位置和运动模型，预测时间t时，物体的位置
  优点：高采样率，低时延，不需要infrastruktur（传感器装在机器人上就好）
  缺点：只有相对位置，有累计误差，位置的不确定度越来越大（经过无数步后，位置的不确定度会趋于无穷大，如果是匀速运动，那么速度的不确定度一直不变）
  步骤：
  – 定义物体坐标系和世界坐标系
  – 计算物体在物体坐标系里的运动：直接从传感器数据得到/ 间接通过运动模型得到
  – 把物体的运动从物体坐标系转移到世界坐标系
  – 从起始点来解释物体的运动-整条轨迹
• 在Koppelnavigation中什么样的传感器会被使用？（基于物体坐标系的测量）
  根据测量的量分类：
  – 测距离：odometry(比如安装在轮滑鞋上的)，相机(如鼠标底下的)
  – 测速度：fiber optic-gyroskop，vibrations-gyroskop
  – 测加速度：integrated accelerometer
  – IMU inertial measurement unit
  根据测量的原理分类：
  – 机械式：轮式里程计
  – 光学式：相机
  – 惯性式：陀螺仪、加速度计
  还可以分为直接测量（位置）、间接测量（速度、加速度）
• 一般的运动模型可以表示为（后面的两项为输入向量）：
  

基础汽车运动学知识

• 理想的汽车：
  汽车本身可视为刚体，轮子可以是驱动/不驱动的，轮子可以是固定或者绕z轴旋转的

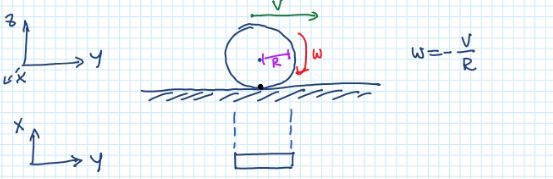
• 理想的车轮：
  圆形车轮，已知半径，与地面只有一个接触点，x和y方向没有滑移，有垂直的转向轴经过接触点和rollaxis（平行于下方坐标系的x方向）
  

• 什么是速度瞬心ICR？
  刚体做平面运动时，瞬时速度为0的某一点，此时，物体上的其他点可以看作在绕其做纯旋转运动。
  对于车轮，每个轮子的瞬心都在它的roll axis上；轮子的速度是一致的consistent with rotation around ICR
  1个交点：绕着这个ICR旋转，有arch trajectory弧线轨迹；平行线：直线轨迹；多个交点：不能运动
  

• 需要考虑的坐标系有哪些？坐标系之间的转换关系？
  已知P在R坐标系中的位姿为${[}^R{x}_p{,}^R{y}_p{,}^R{\theta }_p]$，R在世界坐标系中的位姿为${[}^w{x}_R{,}^w{y}_R{,}^w{\theta }_R]$,求P在世界坐标系中的位姿：

  图示	计算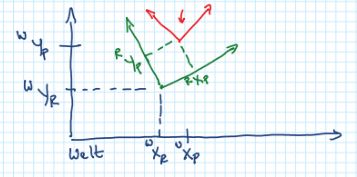

  如果已知P在R坐标系中的速度信息，还可以求出P在世界坐标系中的速度信息：
  $$\left[\begin{array}{c}{}^w{\dot{x}}_p\\ {}^w{\dot{y}}_p\\ {}^w{\dot{\theta }}_p\end{array}\right]=T\left[\begin{array}{c}{}^R{\dot{x}}_p\\ {}^R{\dot{y}}_p\\ {}^R{\dot{\theta }}_p\end{array}\right]$$

• 两轮运动学
  一般来说，两轮的模型可以分成differential drive(这个模型是没有转向角的，差速驱动differential drive利用左右轮的速度差异来旋转，如平衡车）和 wheels with steering wheel. 这两种模型的输入向量可以为：
  
  >> wheels with steering wheel
  

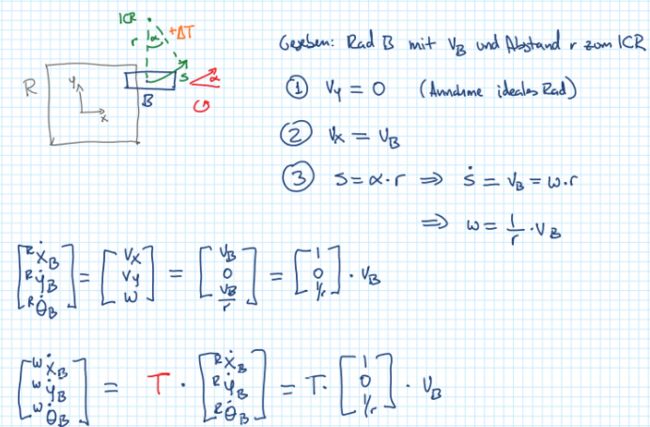
  >> Differential drive
  已知两个左右车轮的速度，求点F的速度和角速度，然后可以求出世界坐标系下的F的速度信息。
  
  

时间离散

为了把一个时间连续的运动模型近似成时间离散的模型，可以有三种方法。假设已知初始位置$x_0=x(t_0)$，求整条轨迹。下面先给出三种方法的粗略对比，然后再给出一些计算过程。

1. 通过一块一块piecewise的绕着ICR的运动来离散化：通过很多个小圆弧拼接起来进行近似。在$t_k$和$t_{k+1}$之间时，ICR是不变的，此时每一段轨迹都是小圆弧
   

2. 通过差分方程 differential equation。分为显式和隐式，隐式通常有更好的稳定性和收敛性
   

3. 解析式的时间离散：就是利用的在时间间隔内积分${\underline{x}}_{k+1}={\underline{x}}_k+{\int }_{t_k}^{t_{k+1}}f(\underline{x}(t),{\mu }_k)dt$
   

法2：基于差分方程

显式欧拉法：
$${\underline{x}}_{k+1}={\underline{x}}_k+{\underline{\dot{x}}}_k\Delta t_k={\underline{x}}_k+f({\underline{x}}_k,{\underline{v}}_k,{\underline{\alpha }}_k)\Delta t_k$$

隐式欧拉法，是一个非线性的系统，可以用高斯牛顿等方法求解：
$${\underline{x}}_{k+1}={\underline{x}}_k+{\underline{\dot{x}}}_{k+1}\Delta t_k={\underline{x}}_k+f({\underline{x}}_{k+1},{\underline{v}}_{k+1},{\underline{\alpha }}_{k+1})\Delta t_k$$

接着前面differential drive的例子，原来时间连续的运动方程可以变为：

法3：基于解析式

利用在时间间隔内积分

线性化运动方程

经过前面的离散化，可以把运动方程写为${\underline{x}}_{k+1}={\underline{x}}_k+f({\underline{x}}_k,{\underline{u}}_k)\Delta t_k=g({\underline{x}}_k,{\underline{u}}_k)$，但是这个形式还是非线性的！所以还需要进行线性化。
方法：围绕${\hat{\underline{x}}}_k,{\hat{\underline{u}}}_k$进行线性化
前提：g($.$)是可微分的differentiable而且可以忽略不计非线性的余量

不确定度的变化

不确定度怎么通过一个线性、时间离散的运动方程进行传播？需要参考最前面关于期望协方差的基础知识。已知状态向量和输入向量的期望和协方差矩阵，而且两者互相独立。而且有${\underline{x}}_{k+1}=A{\underline{x}}_k+B{\underline{u}}_k$，那么有：
$$\begin{gathered} {\hat{\underline{x}}}_{k+1}=A{\hat{\underline{x}}}_k+B{\hat{\underline{u}}}_k \\ {C}_{k+1}^x=A{C}_k^x{A}^T+B{C}_k^u{B}^T \end{gathered}$$

三. Statische Lokalisierung

初识

• Statische Lokalisierung的问题描述：已知路标的全局位置，物体的传感器测到的到路标的位置（路标在物体坐标系的位置），求物体的全局位置。注意这里只是针对某一个时刻进行求解。
  优点：误差不会被传播
  缺点：需要infrastruktur

• 可以用到的传感器？
  – ToF：GPS，ToF相机，laserscanner，ultraschall，lidar
  – visual：彩色相机，红外相机（可以使用marker，arucos，QR等）
  – Radar
  – signal strength：WLAN，Bluetooth

• 基础概念
  残差：状态和估计值的偏差
  误差：状态和真值的偏差

• 什么是测量模型？
  $\underline{y}=h(\underline{x})+v$

• Statische Lokalisierung的过程和举例：
  在有了一个测量结果+已知观测到的路标的绝对位置后，就可以估计出物体的位置；往往会采用多次这个过程，融合多次估计的结果。
  
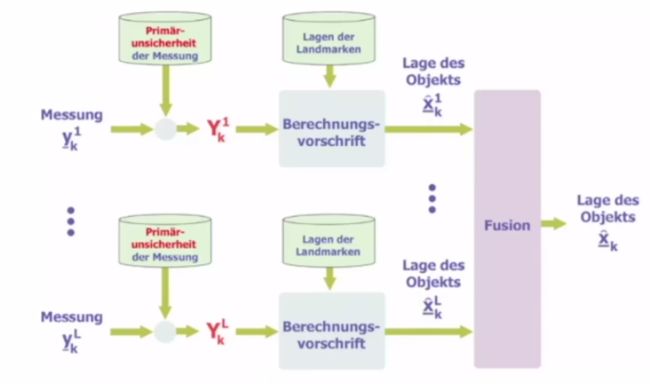
  >> 举例：非线性的例子Trilateration，线性的例子distance to wall
  Trilateration：此处含有模长的计算，是非线性的
  根据到墙面的举例进行定位：已知的是墙面所代表的直线方程normallform（已经归一化了，所以可以按照下图这么求距离），S表示的是距离值。

可以看到，这里的状态$\underline{x}$就是一个2维的向量，而给出了4个方程，所以超定了，可以使用最小二乘法进行求解（这样就可以用到所有的4组数据）

最小二乘法：Batch&Recursive

最小二乘法为什么使用了平方：因为平方可以消除误差正负方向上的差异，单纯的只比较长度。

Batch和Recursive的比较：
Batch法所有的测量值必须要一次全部获得。因为batch的最小二乘法，随着维度的增加，内存消耗会增大（所有的测量值都要存储）(每一次都要重新计算，已知了前100个状态，想求x_101的话，还要全部重新求一次)，而且计算的时候复杂度也会越来越大（计算H^T W^(-1) H时会更加复杂）。但是递归式的方法的复杂度就是常数级别的。

Batch

LSQ-Schätzer für lineare Messabbildungen in geschlossener Form: Blockweise Methode
思路：对于线性最小二乘法的形式，用一阶导等于0来求出最小值的位置。

注意：

• 权重矩阵是$W^{-1}$，是一个正定矩阵（这样才能有最小值）
• 什么时候$\hat{\underline{x}}$有解？当$H^T{W}^{-1}H$可逆的时候，这表示$rank(H)=n$，即H要满秩。
  必要条件： m >= n
  充分条件：rank(H) = n
• 如果说维度n=m（n是$\hat{\underline{x}}$的维度，m是测量值的维度），那么有$\hat{\underline{x}}=H^{-1}y$

Recursive

法一：使用逆的形式。直接按照定义展开之后就可以获得

法二：接着法一，继续化简。使用sherman-morrison-woodbury公式展开第m+1估计值的期望和协方差矩阵的逆：
（）
（）

其他

• $W_{m+1}^{-1},W_{m+1},C_{m+1}^{-1},C_{m+1}$在迭代最小二乘法中表示什么意思？
  $W_{m+1}^{-1}$是${\underline{y}}_{m+1}$的权重
  $W_{m+1}$可以表示为一种${\underline{y}}_{m+1}$的不确定度
  $C_{m+1}^{-1}$是$\widehat{{\underline{x}}_{m+1}}$的权重
  $C_{m+1}$也是一种$\widehat{{\underline{x}}_{m+1}}$的不确定度

• 迭代最小二乘法里面的边界情况如下。换个角度，其实可以把迭代最小二乘法理解为在估计值和测量值之间的一种插值
  

• 除了测量+估计这种用法，还可以把多个估计值当做测量的结果，然后估计出一个更精确的结果（数据融合）
  
  

初始化方法

假设场景为：我们是按照先后顺序每一次获取一组测量数据（niedrige Bandbreite）

Batch法可用

对于batch的方法，可以等待数据，直到第m次，有$H_{1:m}$满秩（这里也可以理解为，前面m组的测量的总维度大于等于估计量${\underline{x}}_k$的维度）。在定位的过程中，可以得到一些中间结果。已知$\underline{y_{1:m}}，$H_{1:m}$，$W_{1:m}^{-1}$，求第m+1次的估计值。

其他替代 Nichtinformatives Vorwissen

使用边界条件，假设初始的协方差矩阵（不确定度）非常大，会有$C_0^{-1}\approx \underline{0}$，$\underline{x_0}$的值可以随便给。在获得了测量值$\underline{y_1}$之后，初始状态值会跳向靠近测量结果的附近。
这个方法在$H_1$矩阵不是满秩的时候，即$H_1^T{W}_1^{-1}{H}_1$不可逆的时候也可以更新！
举例：

Recursive

这里根据前面迭代最小二乘的两种推导方式，也有两种不同的初始化方法。（逆&没有逆）
法一：已知${\underline{x}}_m$，其协方差矩阵的逆是$C_m^{-1}$，还有测量值${\underline{y}}_{m+1}$，其权重矩阵$W_{m+1}^{-1}$，矩阵$H_{m+1}$
这样初始化后，之后求出来的就是：

法二：已知${\underline{x}}_m$，其协方差矩阵是$C_m$，还有测量值${\underline{y}}_{m+1}$，以及矩阵$W_{m+1}$,矩阵$H_{m+1}$
可以发现，$C_m$是越来越小的(估计值的不确定度)

两种迭代方式的对比：

线性化

法一：线性化，然后再从起始点用迭代细化？？？这里就是使用泰勒展开的方法？？
法二：把h()转换为线性的形式，这里举了一个例子：通过距离测量对点状物体进行定位时，如何将非线性测量方程转换为线性测量方程

法一是用两组测量量相减，得到线性化的结果。缺点是，方程数量比使用的测量组数少了1个，对于2维的状态量，就需要至少三组测量结果

法二是用了平方消元法，令状态量的平方和为一个新变量$r^2$，然后再求解这个$r^2$的值。这个方法的优点：对于2维状态量，只需要至少两个测量。

不确定度的变化

随着测量数目的增大，不确定度会越来越小。这里给出了一个1D的例子和普适的推导。

1D举例： 待估变量的期望就是测量值的平均值，期望为$\frac{1}{m}{\sigma }^2$，这里的${\sigma }^2$是测量值的方差。所以求出来的估计量的方差是小于测量值的。测量次数越多，方差越小。

普遍形式：
测量量 $\underline{y}$的协方差矩阵为$C_y$，那么就有：
$$\begin{gathered} E({\underline{x}}^{LSQ})=\hat{\underline{x}}=\underset{K^{\ast }}{(H^T{W}^{-1}H{)}^{-1}{H}^T{W}^{-1}}\underline{y} \\ Cov({\underline{x}}^{LSQ})=C_x=K^{\ast }{C}_y(K^{\ast }{)}^T \end{gathered}$$

特殊情况：当$W^{-1}=I_n,C_y={\sigma }^{2}I$时，有
$$\begin{gathered} Cov({\underline{x}}^{LSQ})=(H^{T}H{)}^{-1}{H}^T{\sigma }^{2}IH(H^{T}H{)}^{-1} \\ ={\sigma }^2(H^{T}H{)}^{-1} \end{gathered}$$

四. Dynamische Lokalisierung

初识

• 什么是Dynamische Lokalisierung：在两个时间点之间对状态使用运动方程进行预测(koppelnavigation)，然后对当前时间点使用测量映射关系来修正结果(statistische Lokalisierung)。以这种交替的状态进行

• 基础概念
  系统噪音（过程噪声）：预测过程中的噪音，表示建模误差。可以和计算机舍入误差（比如说用了浮点，那么会引入1e-7的误差项）、模型的线性化程度、离散化引入误差有关；如果还有输入u的话，输入的误差也会考虑到这里。
  测量噪声：校准过程（测量方程）中的这个噪声的协方差矩阵等于测量值噪声的协方差矩阵，跟选取与传感器的特性有关。

• Dynamische Lokalisierung的问题描述
  这里就是有预测和校正两个过程。
  
  这里给了一个matlab的例子，小车是匀速直线运动，可以通过nichtinformatives vorwissen的方法来最终估计出较准确的状态量。
  以上过程中要注意的一个地方，在修正步骤的时候，其实可以有naive和迭代两类方法。问题描述如下:
  
  直觉上来说，可以使用以下两步，但是这个方法需要$H_k$是满秩的：

  1. 求解batch线性最小二乘问题，${\underline{y}}_k\to {\underline{x}}_k^e$
  2. 把${\underline{x}}_k^e$和${\underline{x}}_{k|k-1}$进行数据融合，得到${\underline{x}}_k$

  当$H_k$不能满秩的时候，就用迭代的方式，也就是在statistische Lokailisierung中涉及到的第二种迭代方式。
  
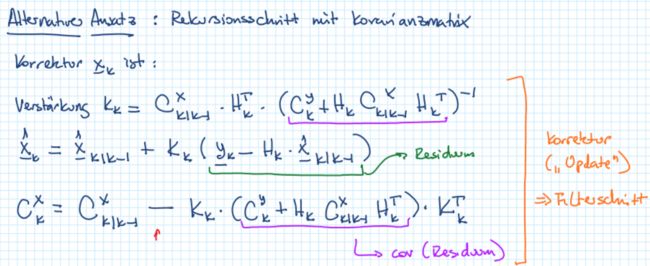
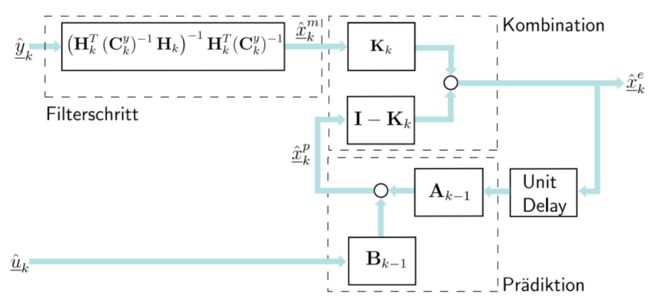
  这两种方法的对比：

  Filterschritt ohne Vorwissen	Filterschritt mit Vorwissen-> Kalman Filterschritt

  不确定度的变化

  预测之后不确定度会变大，但是滤
  波后会变小。很多步之后，总体来说会变小。

  • 传感器的举例-自动驾驶，可以用于定位其他的物体、如行人，汽车
    

BLUE 最优线性无偏估计

基础概念

• 无偏性unbiasedness：估计器的一种属性property。对于一个估计器，如果它的期望值和真值是一样的，那么就可以说这个估计器是无偏的。

• 什么是最优估计器？
  

• 什么是BLUE或者说BLES？ Beste linear erwartungswertreuen Schaetzer

Batch求解的LSQ，令$W_k=C_x^y$时，是最好的线性无偏估计器。因为这种方法，有最小的协方差矩阵（与其他线性无偏估计器相比）

注意！！LSQ with $W_k=C_x^y$ 并不是最好的线性估计器。因为有的估计器可以是有偏的，但是有更小的协方差矩阵。比如:

• 怎么比较协方差矩阵？？？？？?？？？???？？求一个投影，左右分别乘以单位向量e, $e^T$，其实是求这个协方差矩阵中，所有元素的和？？？？

为什么让$\underline{y}$的协方差矩阵作为权重矩阵，即$w_k=C_k^y$

A：batch LSQ with $W_k=C_k^y$ has the ‘minimal’ covariance matrix under all linear unbiased estimator.

证明过程：假设一个线性/映射估计器，用无偏的形式代入，注意下面的$K_k^{LSQ}$和卡尔曼滤波里的K不是一个东西。

想要一个估计器无偏，就要满足$E({\underline{x}}_k^e)=E({\underline{x}}_k^e)=E({\underline{x}}_k)=\widehat{{\underline{x}}_k}$

接下来就可以把batch求解LSQ的结果代入矩阵K中，这里就可以发现，这个线性估计器一定是无偏的。为了证明是BLUE，就还要检查协方差矩阵是最小的，即对于其他估计器都有，$Cov({\underline{x}}_k^e)\ge Cov({\underline{x}}_k^{LSQ})$。在计算上面两个协方差的时候就要把$W_k=C_k^y$带进去，就可以证明出$Cov({\underline{x}}_k^{LSQ})$是最小的。

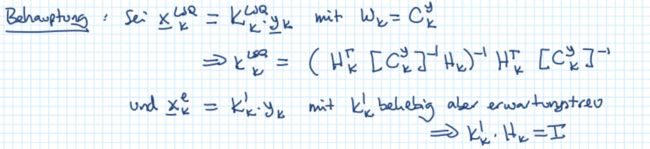
哪些情况可以实现BLUE

先上表格总结需要满足的条件：

Filterschritt ohne Vorwissen	Fusionierung	Rekursive

前面两条和在一起可以是一个optimale Filterschritt.

1. Filterschritt ohne Vorwissen mit dem LSQ-Blockverfahren(证明过程在上一条)
2. Fusionierung mit dem Blockverfahren von LSQ
3. Rekursive LSQ

• Fusionierung mit LSQ：照猫画虎第一条，把测量映射都变成1，测量量的协方差矩阵也都变成估计量的协方差矩阵。套进去求解出来的${\underline{x}}^{LSQ}$就是最好的线性无偏估计器的结果(就是协方差矩阵加权的形式,分子是错开对应的)。注意这里必须要有不同的估计量之间是独立的，权重矩阵是个对角阵。
  
  这里也可以看一下如果是一般形式的线性估计器，需要达到什么条件才可以变成BLUE：
  
  上面证明了无偏，下面来证明协方差最小**（协方差矩阵的迹最小时，有$K_{opt}$）**：
  
  求解出来$K_{opt}=C_2^x(C_1^x+C_2^x{)}^{-1}=K_1^{LSQ}$，根据无偏要满足的要求就有$K_2=I-K_1=K_2^{LSQ}$

• Rekursive LSQ的证明
  无偏的部分：可以得到$K_k^1+K_k^2{H}_k=I$,是满足下面的结论的。
  
  求协方差最小：这里取了一个模长为1的列向量。为了最小化函数，用了一阶导等于0的方法。求出来的$K_k^{opt}=K_k^{rek}$
  

卡尔曼滤波器

线性、时间离散的运动方程的预测+迭代的Filterschritt就是卡尔曼滤波器

卡尔曼滤波器的复杂度不会随着时间或者测量量数量的增加而增加，预测和估计时，都只会使用期望和协方差矩阵来存储信息，并将其传递到下一个步骤进行处理。参考期望和协方差矩阵的维度。

数据的关联

测量值之间或者估计值之间的依赖性(不独立)从何而来？

1. 平滑glättung
2. 内外插值 Inter/Extrapolierung
3. 数据增强

有了相互依赖的关系的话，协方差矩阵就会变为:
$$Cov(\left[\begin{array}{c}a\\ b\end{array}\right])=\left[\begin{array}{cc}{C}_a& C_{ab}\\ C_{ba}& C_b\end{array}\right]$$

如果忽略数据的依赖关系，会有什么后果？
举个例子，在BLUE时，我们要使用测量值的协方差矩阵作为测量误差的协方差，如果此时我们忽略了数据之间的依赖关系，只使用对角阵作为测量误差的协方差矩阵（简化了矩阵），那么想有BLUE的条件就是不成立的，也就是说我们此时只能得到次优的结果。
举例：如果使用了相关的数据，可以得到一个更小的协方差矩阵，但是这个矩阵的结果是错误的！！要参考Folie的例子。

五. SLAM

初识

• 什么是SLAM
  simultaneous localization and mapping
  通过landmark来定位机器人
  通过机器人实时的位置来定位landmark

• SLAM的挑战在哪里

  1. landmark也成为了状态量的一部分，复杂度，就是O(landmark数量的^3)

  2. 通常来说，都是非线性的

  3. 通常都有数据关联问题：如果不知道测量值y_k是从哪个landmark测出来的，要怎么办呢？
     –法一：naive：找到和测量值距离最近的landmark，但是这种方法没有到考虑不确定度
     –法二：使用Mahalanobis距离。最小化残差
     

  4. 没有绝对的起始位置

  5. 所有的landmark都是相互关联的correlate。如果L1可以通过L6进行correct，那么所有的Landmark都可以被修正，而且整体的不确定度会变小。loop closure
     

  6. 在没有landmark的情况下，相当于是纯koppelnavigation, 不确定度就会一直增加且without limits. 只有在有新landmark被观察到的时候才能同时更新位姿和landmark(之前观测到的也会被korrected)的位置。

• 为什么估计的地标位置之间的依赖关系在这里很重要？
  如果可以形成回环，就可以减小整体的误差。

• SLAM可以分为online SLAM和full SLAM。online的只会估计当前机器人的位置和路标的位置，full的会估计整个轨迹，修正之前的所有机器人位置和路标位置。Online SLAM的初始化如下。预测步骤中，协方差矩阵C，路标对应的方差是0， 因为路标是固定不动的。
  
  

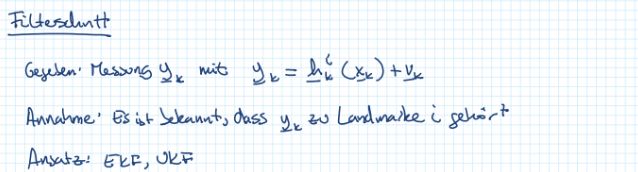
非线性情况的求解

预测步骤：

Filterschritt步骤：

• 使用泰勒展开在${\underline{x}}_k^0$处线性化，然后按照Block的方法求解。注意：${\hat{\underline{x}}}_k^0$要尽可能靠近${\hat{\underline{x}}}_k$

• 线性化之后，使用迭代的方式（EKF）
  
  如果碰到在${\underline{x}}_k^P$点附近线性化程度不好的情况，为了过更加准确，可以使用UKF

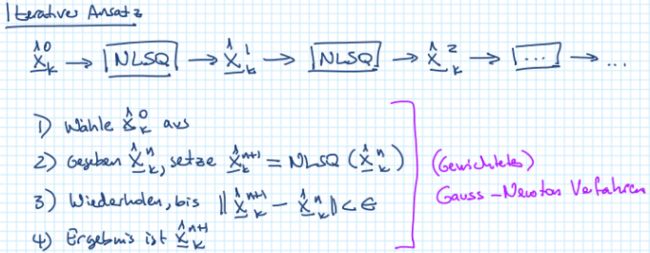
• 或者可以用迭代的方式，即使用非线性最小二乘求解：高斯牛顿法。NLSQ的初值${\hat{\underline{x}}}_k^0$选择非常重要，最好是离${\underline{x}}_k^{wahr}$很近。一般来说，NLSQ不是最优的，但是也足够好了。当然，这个方法也可能陷入局部最小值。