决策树(decision tree)理论+Python代码实现

1. 什么是决策树/判定树?

2. 信息如何度量？

3. 算法理论

4. python代码实现

5.树剪枝叶(避免overfitting)

6.优缺点

1.什么是决策树/判定树（decision tree)?

决策树就是运用已知的现有信息，构造属性流程图建立模型，为包含相同属性信息的事物做预测，并使预测准确率最大。
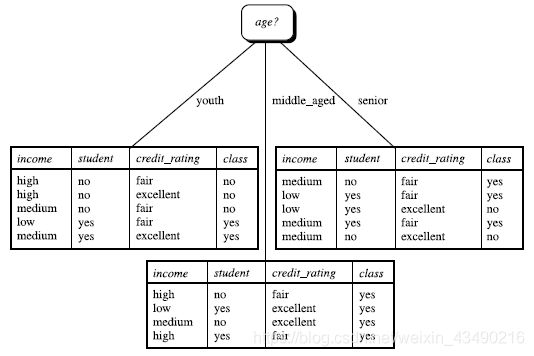
决策树/判定树是一个类似于流程图的树结构：

• 每个内部结点表示在一个属性上的测试
• 每个分支代表一个属性输出
• 每个树叶结点代表类或类分布
• 树的最顶层是根结点

样本属性较多，如何在每一步选择合适的样本属性信息对未标签样本进行判别？
以根节点信息熵为基准，分别度量样本各个属性的信息熵，选取样本属性中信息熵最小的，同时也是使根节点样本信息熵增益最大的属性为依据作为划分样本的结点，构造决策树，对未标签的样本进行最有效判别

2. 信息如何度量？

信息用信息熵(entropy)度量:
1948年，香农提出了 ”信息熵(entropy)“的概念
借鉴热力学概念:信息源发送什么符号具有不确定性，可用概率来度量

• 符号说明：

$$符号发生概率：p$$
$$不确定性函数：f(p)$$

• $f\left(p\right)$函数性质

可加性：
两个独立符号所产生的不确定性等于各自吧不确定性之和f(p1p2)=f(p1)+f(p2)
f是p的减函数
p越大，说明符号发生的可能性却大，不确定性函数越小。
对数函数满足上面两个性质

• 建立假设：

$f\left(p\right)$=log($\frac{1}{p}$)
信息源中要考虑所有可能发生情况的平均不确定性
若信息符号有n种取值：u1,u2,…,un
对应概率：p1,p2,…,pn
各种符号出现概率彼此独立
信源的平均不确定性：H(u)=E(log$\frac{1}{pi}$)=$\sum _{i=1}^{n}pi\ast log(\frac{1}{pi})$
一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息==>信息量的度量就等于不确定性的多少
比特(bit)来衡量信息的多少, 变量的不确定性越大，概率越小，熵也就越大
H(X)= −∑p(x)logp(x)（x∈χ）

3.决策树归纳算法 （ID3）

1970-1980， J.Ross. Quinlan, ID3算法
选择属性判断结点
信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D)
通过A来作为节点分类获取了多少信息
区别：属性选择度量方法不同： C4.5 （gain ratio), CART(gini index), ID3 (Information Gain)

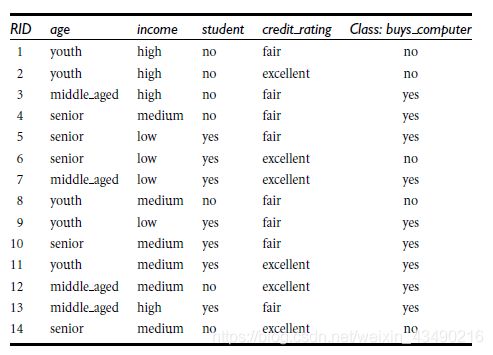
9个“yes”,5个“no”
$Info(D)=-\frac{9}{14}lo{g}_2(\frac{9}{14})-\frac{5}{14}lo{g}_2(\frac{5}{14})=0.940bits$
以age属性进行划分

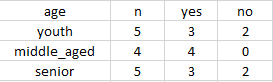
\begin{align}
Info_age(D)=5/14(-\dfrac{2}{5}log_2(\dfrac{2}{5})-\dfrac{3}{5}log_2(\dfrac{3}{5})) \
& + 4/14(-\dfrac{4}{4}log_2(\dfrac{4}{4})-\dfrac{0}{4}log_2(\dfrac{0}{4})) \
& + 5/14(-\dfrac{3}{5}log_2(\dfrac{3}{5})-\dfrac{2}{5}log_2(\dfrac{2}{5})) \
& =0.694bits\
\end{align}

以income属性进行划分

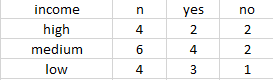
\begin{align}
Info_income(D)=4/14(-\dfrac{2}{4}log_2(\dfrac{2}{4})-\dfrac{2}{4}log_2(\dfrac{2}{4})) \
& + 6/14(-\dfrac{4}{6}log_2(\dfrac{4}{6})-\dfrac{2}{6}log_2(\dfrac{2}{6})) \
& + 4/14(-\dfrac{3}{4}log_2(\dfrac{3}{4})-\dfrac{1}{4}log_2(\dfrac{1}{4})) \
& =0.911bits\
\end{align}

以student属性进行划分

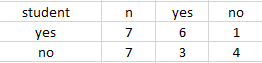
\begin{align}
Info_student(D)=7/14(-\dfrac{6}{7}log_2(\dfrac{6}{7})-\dfrac{1}{7}log_2(\dfrac{1}{7})) \
& + 7/14(-\dfrac{3}{7}log_2(\dfrac{3}{7})-\dfrac{4}{7}log_2(\dfrac{4}{7})) \
& =0.788bits\
\end{align}

以credit_rating属性进行划分

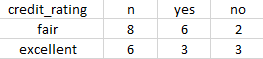
\begin{align}
Info_creditrating(D)=8/14(-\dfrac{6}{8}log_2(\dfrac{6}{8})-\dfrac{2}{8}log_2(\dfrac{2}{8})) \
& + 3/6(-\dfrac{3}{6}log_2(\dfrac{3}{6})-\dfrac{3}{6}log_2(\dfrac{3}{6})) \
& =0.892bits\
\end{align}

算法：
树以代表训练样本的单个结点开始（步骤1）。
如果样本都在同一个类，则该结点成为树叶，并用该类标号（步骤2 和3）。
否则，算法使用称为信息增益的基于熵的度量作为启发信息，选择能够最好地将样本分类的属性（步骤6）。该属性成为该结点的“测试”或“判定”属性（步骤7）。在算法的该版本中，
所有的属性都是分类的，即离散值。连续属性必须离散化。
对测试属性的每个已知的值，创建一个分枝，并据此划分样本（步骤8-10）。
算法使用同样的过程，递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上，就不必该结点的任何后代上考虑它（步骤13）。
递归划分步骤仅当下列条件之一成立停止：
(a) 给定结点的所有样本属于同一类（步骤2 和3）。
(b) 没有剩余属性可以用来进一步划分样本（步骤4）。在此情况下，使用多数表决（步骤5）。
这涉及将给定的结点转换成树叶，并用样本中的多数所在的类标记它。替换地，可以存放结
点样本的类分布。
(c) 分枝
test_attribute = a i 没有样本（步骤11）。在这种情况下，以 samples 中的多数类
创建一个树叶（步骤12）

4. python代码实现

本次代码的环境：

运行平台： Windows
Python版本： conda
IDE： eclipse
在eclipse下使用conda编辑器可以成功运行，但在pycharm中运行失败。

使用scikit-learn
安装scikit-learn: pip, easy_install, windows installer
安装必要package：numpy， SciPy和matplotlib，
可使用Anaconda (包含numpy, scipy等科学计算常用package）
安装 Graphviz： http://www.graphviz.org/
配置环境变量
转化dot文件至pdf可视化决策树在cmd输入：dot -Tpdf iris.dot -o output.pdf
(dot需为utf-8类型编码，建议存为txt形式(保存时选utf-8形式)然后dot -Tpdf iris.txt -o output.pdf )
iris.txt 为保存的文件路径，output.pdf为输出文件的路径

# coding:utf-8
from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import tree
from sklearn import preprocessing
from sklearn.externals.six import StringIO
imort os
# Read in the csv file and put features into list of dict and list of class label
allElectronicsData = open(r'C:\Users\66\Desktop\一深度学习\代码与素材\01DTree\AllElectronics.csv', 'rt')
reader=csv.reader(allElectronicsData)
headers=next(reader)
print(headers)
featureList=[]
labelList=[]
for row in reader:
    labelList.append(row[len(row)-1])# read the last column
    rowDict = {}
    for i in range(1, len(row)-1):
        rowDict[headers[i]] = row[i]# read sample
    featureList.append(rowDict)    
print(featureList)#transform sample str to list[dic,],then use DictVectorizer to be array.
# Vetorize features
vec = DictVectorizer()
dummyX = vec.fit_transform(featureList) .toarray()
print("dummyX: " + str(dummyX))
print(vec.get_feature_names())
print("labelList: " + str(labelList))
# vectorize class labels
lb = preprocessing.LabelBinarizer()
dummyY = lb.fit_transform(labelList)
print("dummyY: " + str(dummyY))
# Using decision tree for classification
# clf = tree.DecisionTreeClassifier()
clf = tree.DecisionTreeClassifier(criterion='entropy')
clf = clf.fit(dummyX, dummyY)
print("clf: " + str(clf))# explain the  clf function
# Visualize model
with open(r'D:\tree0.dot','w',encoding='utf-8') as f:
   f=tree.export_graphviz(clf,feature_names=vec.get_feature_names(),out_file=f)
oneRowX = dummyX[0:2, :]
print("oneRowX: " + str(oneRowX))
newRowX = oneRowX
newRowX[0][0] = 1
newRowX[0][2] = 0
print("newRowX: " + str(newRowX))
predictedY = clf.predict(newRowX)
print("predictedY: " + str(predictedY))
os.system("dot -Tpdf D:/tree0.dot -o D:/tree0.pdf")
#os.system("dot -Tpdf iris.dot -o outpu.pdf")
#iris.dot is the name of the name of dot ,outpu is the name of output file

5. 树剪枝叶 （避免overfitting)

• 先剪枝
• 后剪枝

6. 决策树的优缺点

• 直观，便于理解，小规模数据集有效
• 处理连续变量不好
  类别较多时，错误增加的比较快
  可规模性一般