交叉梯度函数的MATLAB实现及代码分享02

交叉梯度函数的MATLAB实现及代码分享02

交叉梯度函数可用于反演成像中。作为一个连接不同物性参数的桥梁，交叉梯度函数可以实现不同物性参数的联合反演成像。

本文是对上一个博文的补充，详见交叉梯度函数的MATLAB实现及代码分享01，上一篇博文主要是二维的交叉梯度函数，本文分享三维的交叉梯度函数的MATLAB实现及代码。

一、交叉梯度函数的定义

三维情况下，交叉梯度函数定义为：

交叉梯度函数在三个方向上的分量定义为：
1、x方向分量；

2、y方向分量；

3、z方向分量；

采用中心差分的形式对交叉梯度函数进行离散：

采用中心差分的方式对三维交叉梯度函数在三个分量上分别离散：
1、x方向上交叉梯度函数离散；

2、y方向上交叉梯度函数离散；

3、z方向上交叉梯度函数离散；

分别计算出交叉梯度函数三个分量的值，对三个分量上的值取平方和再开平方，即可得到三维情况下的交叉梯度函数值。

根据上式即可编程实现交叉梯度函数的计算。

二、交叉梯度函数的性质

在数学中，我们知道：
1） 标量场中某一点上的梯度指向标量场在这一点处增长最快的方向，梯度的大小是标量场在这一点最大的变化率；
2） 两个向量叉乘的模等于两个向量的模的乘积乘以sinθ，其中θ是两个向量的夹角。如果两个向量平行，那么夹角是0°或者180°，sinθ等于零，此时两个向量的叉乘等于零。

将数学角度的理解推广到地球物理领域，可以比较容易得出交叉梯度函数用于地球物理联合反演的理论基础：
1） 当用于联合反演的两种物性参数变化方向平行（相同或者相反），或者其中某一种物性参数不发生变化时，两者的交叉梯度函数等于零；

2） 当用于联合反演的两种物性参数的变化方向不同时，两者的交叉梯度函数不等于零。

以上两条结论就是交叉梯度函数在联合反演中能够有所应用的原理基础。在联合反演的目标函数中，当满足交叉梯度函数等于0时，则表示参与运算的两种物性变化方向平行或者其中之一不变化，也就是说两种物性所反映的地质体存在着结构上的相似性，也即存在着共同的物性边界。
在联合反演算法中引入交叉梯度函数，其会从结构上构建起两种参数之间的关系，对反演起约束，使得最终反演结果向两种物性所反映的共同边界变化，有效提高反演结果的精确性。

三、模型算例

建立了几组数值模型，来充分的认识一下交叉梯度函数。分别建立两种不同物性参数（电磁波吸收系数模型、地震波速度模型），计算他们的交叉梯度函数值。

模型一

电磁波吸收系数分布图：

地震波速度分布图：

交叉梯度函数值分布图：

模型二

电磁波吸收系数分布图：

地震波速度分布图：


交叉梯度函数值分布图：


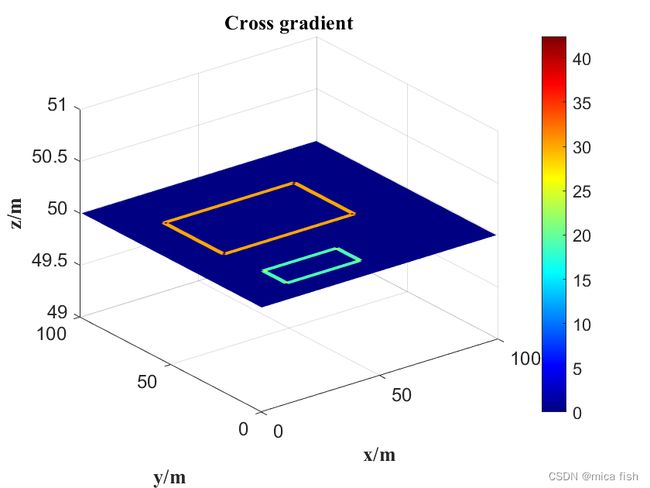
三维图片的可视化不是很直观，我尽量的对代码进行调整，将我们的计算结果展现出来，详细的理解还是需要看二维的交叉梯度函数，三维交叉梯度函数性质与二维交叉梯度函数性质一致。

四、MATLAB代码分享

% 计算交叉梯度函数

tao3d = zeros(nex,ney,nez);
tao3dx = zeros(nex,ney,nez);
tao3dy = zeros(nex,ney,nez);
tao3dz = zeros(nex,ney,nez);


for i = 2:ney-1
    for j = 2:nex-1
        for k = 2:nez-1
            tao3dx(i,j,k) = (alpha3d(i,j+1,k)-alpha3d(i,j-1,k))/(2*dy)*...
                (vel3d(i,j,k+1)-vel3d(i,j,k-1))/(2*dz) - ...
                (alpha3d(i,j,k+1)-alpha3d(i,j,k-1))/(2*dz)*...
                (vel3d(i,j+1,k)-vel3d(i,j-1,k))/(2*dy);
            tao3dy(i,j,k) = (alpha3d(i,j,k+1)-alpha3d(i,j,k-1))/(2*dz)*...
                (vel3d(i+1,j,k)-vel3d(i-1,j,k))/(2*dx) - ...
                (alpha3d(i+1,j,k)-alpha3d(i-1,j,k))/(2*dx)*...
                (vel3d(i,j,k+1)-vel3d(i,j,k-1))/(2*dz);
            tao3dz(i,j,k) = (alpha3d(i+1,j,k)-alpha3d(i-1,j,k))/(2*dx)*...
                (vel3d(i,j+1,k)-vel3d(i,j-1,k))/(2*dy) - ...
                (alpha3d(i,j+1,k)-alpha3d(i,j-1,k))/(2*dy)*...
                (vel3d(i+1,j,k)-vel3d(i-1,j,k))/(2*dx);
        end
    end
end
tao3d = sqrt(tao3dx.^2+tao3dy.^2+tao3dz.^2);