【图像分割】灰狼算法最小交叉熵多阈值图像分割【含Matlab源码 903期】
⛄一、最小交叉熵多阈值图像分割简介
1 单阈值分割
设有两个概率分布P={p1, p2, …, pN}和Q={q1, q2, …, qN}, 交叉熵度量它们之间的信息量差异。其对称形式为
![]()
交叉熵既可看成是采用P取代Q作为单个系统概率分布时系统信息量变化的期望值, 也可看成是两个概率系统P和Q之间的信息量差异。因而可用最小交叉熵准则实现系统的概率分布估计或逼近。
现有的最小交叉熵分割方法原理是用P和Q分别表征分割前后的原始图和分割图;然后计算目标之间的交叉熵、背景之间的交叉熵;并取其和定义为原始图和分割图之间的交叉熵, 求最优阈值使交叉熵最小。
单阈值分割方法具体实现如下:
设阈值t 将原始图像 (L个灰度级) 的图像分为目标和背景两类, 图像一维直方图为h (i) (1, 2, …, L) , 令

则交叉熵判别函数定义为
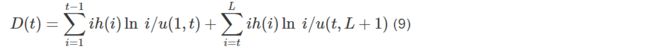
其中:i是灰度值; t是阈值化时的阈值;u (1, t) 和u (t, L+1) 是类内均值, 分别代表分割后得到的分割图中目标和背景的灰度。
图像的最佳阈值:
t*=arg mint{D (t) } (10)
2 多阈值分割法
对复杂图像或者含有多个物体的图像进行分割处理, 需要用到多阈值分割, 可在前述单阈值的基础上进行推广, 将一维交叉熵应用于多阈值分割。设t1, t2, …, tn是分割阈值, 且有t1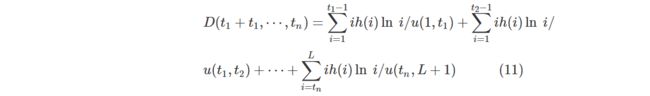
图像的最佳阈值:
(t1, t2, …, t*n) =arg mint{D (t1, t2, …, tn) } (12)
⛄二、部分源代码
%% 基于灰狼算法的最小交叉熵多阈值分割
clear all;
clc
rng(‘default’);
I = imread(‘lena.jpg’);%读取图像
SearchAgents_no=50; %种群数量
Max_iteration=100; % 最大迭代次数
dim = 4;%阈值个数
lb = ones(1,dim); %下边界1
ub = 255.*ones(1,dim);%上边界255
fobj =@(thresh)fun(I,thresh);%适应度函数
[Best_score,Best_pos,GWO_cg_curve]=GWO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
% Grey Wolf Optimizer
function [Alpha_score,Alpha_pos,Convergence_curve]=GWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,dim);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,dim);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,dim);
Delta_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
l=0;% Loop counter
% Main loop
while l
% Return back the search agents that go beyond the boundaries of the search space
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)Alpha_score && fitnessAlpha_score && fitness>Beta_score && fitness ⛄三、运行结果
![]()
![]()
![]()
⛄四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1]赵勇,方宗德,庞辉,王侃伟.基于量子粒子群优化算法的最小交叉熵多阈值图像分割[J].计算机应用研究. 2008,(04)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除