深度学习 超参数调整【转】

Markdown Revision 1;
Editor: 乔成磊-同济大学，王超锋
Contact: [email protected]，[email protected]
Updater: sjsdfg，王超锋

14.1 写在前面

　　关于训练深度学习模型最难的事情之一是你要处理的参数的数量。无论是从网络本身的层宽（宽度）、层数（深度）、连接方式，还是损失函数的超参数设计和调试，亦或者是学习率、批样本数量、优化器参数等等。这些大量的参数都会有网络模型最终的有效容限直接或者间接的影响。面对如此众多的参数，如果我们要一一对其优化调整，所需的无论是时间、资源都是不切实际。结果证实一些超参数比其它的更为重要，因此认识各个超参数的作用和其可能会造成的影响是深度学习训练中必不可少的一项重要技能。

​ 目前，超参数调整一般分为手动调整和自动优化超参数两种。本章节不会过多阐述所有超参数的详细原理，如果需要了解这部分，您可以翻阅前面的基础章节或者查阅相关文献资料。当然，下面会讲到的一些超参数优化的建议是根据笔者们的实践以及部分文献资料得到认知建议，并不是非常严格且一定有效的，很多研究者可能会很不同意某些的观点或有着不同的直觉，这都是可保留讨论的，因为这很依赖于数据本身情况。

14.2 超参数概述

14.2.1 什么是超参数，参数和超参数的区别

​ 区分两者最大的一点就是是否通过数据来进行调整，模型参数通常是有数据来驱动调整，超参数则不需要数据来驱动，而是在训练前或者训练中人为的进行调整的参数。例如卷积核的具体核参数就是指模型参数，这是有数据驱动的。而学习率则是人为来进行调整的超参数。这里需要注意的是，通常情况下卷积核数量、卷积核尺寸这些也是超参数，注意与卷积核的核参数区分。

14.2.2 神经网络中包含哪些超参数

　　 通常可以将超参数分为三类：网络参数、优化参数、正则化参数。

​ 网络参数：可指网络层与层之间的交互方式（相加、相乘或者串接等）、卷积核数量和卷积核尺寸、网络层数（也称深度）和激活函数等。

​ 优化参数：一般指学习率（learning rate）、批样本数量（batch size）、不同优化器的参数以及部分损失函数的可调参数。

​ 正则化：权重衰减系数，丢弃法比率（dropout）

14.2.3 模型优化寻找最优解和正则项之间的关系

​ 网络模型优化调整的目的是为了寻找到全局最优解（或者相比更好的局部最优解），而正则项又希望模型尽量拟合到最优。两者通常情况下，存在一定的对立，但两者的目标是一致的，即最小化期望风险。模型优化希望最小化经验风险，而容易陷入过拟合，正则项用来约束模型复杂度。所以如何平衡两者之间的关系，得到最优或者较优的解就是超参数调整优化的目的。

14.2.4 超参数的重要性顺序

• 首先， 学习率，损失函数上的可调参数。在网络参数、优化参数、正则化参数中最重要的超参数可能就是学习率了。学习率直接控制着训练中网络梯度更新的量级，直接影响着模型的有效容限能力；损失函数上的可调参数，这些参数通常情况下需要结合实际的损失函数来调整，大部分情况下这些参数也能很直接的影响到模型的的有效容限能力。这些损失一般可分成三类，第一类辅助损失结合常见的损失函数，起到辅助优化特征表达的作用。例如度量学习中的Center loss，通常结合交叉熵损失伴随一个权重完成一些特定的任务。这种情况下一般建议辅助损失值不高于或者不低于交叉熵损失值的两个数量级；第二类，多任务模型的多个损失函数，每个损失函数之间或独立或相关，用于各自任务，这种情况取决于任务之间本身的相关性，目前笔者并没有一个普适的经验由于提供参考；第三类，独立损失函数，这类损失通常会在特定的任务有显著性的效果。例如RetinaNet中的focal loss，其中的参数γ，α，对最终的效果会产生较大的影响。这类损失通常论文中会给出特定的建议值。

• 其次，批样本数量，动量优化器（Gradient Descent with Momentum）的动量参数β。批样本决定了数量梯度下降的方向。过小的批数量，极端情况下，例如batch size为1，即每个样本都去修正一次梯度方向，样本之间的差异越大越难以收敛。若网络中存在批归一化（batchnorm），batch size过小则更难以收敛，甚至垮掉。这是因为数据样本越少，统计量越不具有代表性，噪声也相应的增加。而过大的batch size，会使得梯度方向基本稳定，容易陷入局部最优解，降低精度。一般参考范围会取在[1:1024]之间，当然这个不是绝对的，需要结合具体场景和样本情况；动量衰减参数β是计算梯度的指数加权平均数，并利用该值来更新参数，设置为 0.9 是一个常见且效果不错的选择；

• 最后，Adam优化器的超参数、权重衰减系数、丢弃法比率（dropout）和网络参数。在这里说明下，这些参数重要性放在最后并不等价于这些参数不重要。而是表示这些参数在大部分实践中不建议过多尝试，例如Adam优化器中的β1，β2，ϵ，常设为 0.9、0.999、10−8就会有不错的表现。权重衰减系数通常会有个建议值，例如0.0005 ，使用建议值即可，不必过多尝试。dropout通常会在全连接层之间使用防止过拟合，建议比率控制在[0.2,0.5]之间。使用dropout时需要特别注意两点：一、在RNN中，如果直接放在memory cell中,循环会放大噪声，扰乱学习。一般会建议放在输入和输出层；二、不建议dropout后直接跟上batchnorm，dropout很可能影响batchnorm计算统计量，导致方差偏移，这种情况下会使得推理阶段出现模型完全垮掉的极端情况；网络参数通常也属于超参数的范围内，通常情况下增加网络层数能增加模型的容限能力，但模型真正有效的容限能力还和样本数量和质量、层之间的关系等有关，所以一般情况下会选择先固定网络层数，调优到一定阶段或者有大量的硬件资源支持可以在网络深度上进行进一步调整。

14.2.5 部分超参数如何影响模型性能

超参数	如何影响模型容量	原因	注意事项
学习率	调至最优，提升有效容量	过高或者过低的学习率，都会由于优化失败而导致降低模型有效容限	学习率最优点，在训练的不同时间点都可能变化，所以需要一套有效的学习率衰减策略
损失函数部分超参数	调至最优，提升有效容量	损失函数超参数大部分情况都会可能影响优化，不合适的超参数会使即便是对目标优化非常合适的损失函数同样难以优化模型，降低模型有效容限。	对于部分损失函数超参数其变化会对结果十分敏感，而有些则并不会太影响。在调整时，建议参考论文的推荐值，并在该推荐值数量级上进行最大最小值调试该参数对结果的影响。
批样本数量	过大过小，容易降低有效容量	大部分情况下，选择适合自身硬件容量的批样本数量，并不会对模型容限造成。	在一些特殊的目标函数的设计中，如何选择样本是很可能影响到模型的有效容限的，例如度量学习（metric learning）中的N-pair loss。这类损失因为需要样本的多样性，可能会依赖于批样本数量。
丢弃法	比率降低会提升模型的容量	较少的丢弃参数意味着模型参数量的提升，参数间适应性提升，模型容量提升，但不一定能提升模型有效容限
权重衰减系数	调至最优，提升有效容量	权重衰减可以有效的起到限制参数变化的幅度，起到一定的正则作用
优化器动量	调至最优，可能提升有效容量	动量参数通常用来加快训练，同时更容易跳出极值点，避免陷入局部最优解。
模型深度	同条件下，深度增加，模型容量提升	同条件，下增加深度意味着模型具有更多的参数，更强的拟合能力。	同条件下，深度越深意味着参数越多，需要的时间和硬件资源也越高。
卷积核尺寸	尺寸增加，模型容量提升	增加卷积核尺寸意味着参数量的增加，同条件下，模型参数也相应的增加。

14.2.6 部分超参数合适的范围

超参数	建议范围	注意事项
初始学习率	SGD: [1e-2, 1e-1] momentum: [1e-3, 1e-2] Adagrad: [1e-3, 1e-2] Adadelta: [1e-2, 1e-1] RMSprop: [1e-3, 1e-2] Adam: [1e-3, 1e-2] Adamax: [1e-3, 1e-2] Nadam: [1e-3, 1e-2]	这些范围通常是指从头开始训练的情况。若是微调，初始学习率可在降低一到两个数量级。
损失函数部分超参数	多个损失函数之间，损失值之间尽量相近，不建议超过或者低于两个数量级	这是指多个损失组合的情况，不一定完全正确。单个损失超参数需结合实际情况。
批样本数量	[1:1024]	当批样本数量过大(大于6000)或者等于1时，需要注意学习策略或者BN的替代品。
丢弃法比率	[0, 0.5]
权重衰减系数	[0, 1e-4]
卷积核尺寸	[7x7],[5x5],[3x3],[1x1], [7x1,1x7]

14.3 网络训练中的超参调整策略

14.3.1 如何调试模型？

在讨论如何调试模型之前，我们先来纠正一个误区。通常理解如何调试模型的时候，我们想到一系列优秀的神经网络模型以及调试技巧。但这里需要指出的是数据才是模型的根本，如果有一批质量优秀的数据，或者说你能将数据质量处理的很好的时候，往往比挑选或者设计模型的收益来的更大。那在这之后才是模型的设计和挑选以及训练技巧上的事情。

1、探索和清洗数据。探索数据集是设计算法之前最为重要的一步，以图像分类为例，我们需要重点知道给定的数据集样本类别和各类别样本数量是否平衡，图像之间是否存在跨域问题（例如网上爬取的图像通常质量各异，存在噪声）。若是类别数远远超过类别样本数（比如类别10000，每个类别却只有10张图像），那通常的方法可能效果并不显著，这时候few-shot learning或者对数据集做进一步增强可能是你比较不错的选择。再如目标检测，待检测目标在数据集中的尺度范围是对检测器的性能有很大影响的部分。因此重点是检测大目标还是小目标、目标是否密集完全取决于数据集本身。所以，探索和进一步清洗数据集一直都是深度学习中最重要的一步。这是很多新手通常会忽略的一点。

2、探索模型结果。探索模型的结果，通常是需要对模型在验证集上的性能进行进一步的分析，这是如何进一步提升模型性能很重要的步骤。将模型在训练集和验证集都进行结果的验证和可视化，可直观的分析出模型是否存在较大偏差以及结果的正确性。以图像分类为例，若类别间样本数量很不平衡时，我们需要重点关注少样本类别在验证集的结果是否和训练集的出入较大，对出错类别可进一步进行模型数值分析以及可视化结果分析，进一步确认模型的行为。

3、监控训练和验证误差。首先很多情况下，我们忽略代码的规范性和算法撰写正确性验证，这点上容易产生致命的影响。在训练和验证都存在问题时，首先请确认自己的代码是否正确。其次，根据训练和验证误差进一步追踪模型的拟合状态。若训练数据集很小，此时监控误差则显得格外重要。确定了模型的拟合状态对进一步调整学习率的策略的选择或者其他有效超参数的选择则会更得心应手。

4、反向传播数值的计算，这种情况通常适合自己设计一个新操作的情况。目前大部分流行框架都已包含自动求导部分，但并不一定是完全符合你的要求的。验证求导是否正确的方式是比较自动求导的结果和有限差分计算结果是否一致。所谓有限差分即导数的定义，使用一个极小的值近似导数。

 

14.3.2 为什么要做学习率调整?

​ 学习率可以说是模型训练最为重要的超参数。通常情况下，一个或者一组优秀的学习率既能加速模型的训练，又能得到一个较优甚至最优的精度。过大或者过小的学习率会直接影响到模型的收敛。我们知道，当模型训练到一定程度的时候，损失将不再减少，这时候模型的一阶梯度接近零，对应Hessian 矩阵通常是两种情况，一、正定，即所有特征值均为正，此时通常可以得到一个局部极小值，若这个局部极小值接近全局最小则模型已经能得到不错的性能了，但若差距很大，则模型性能还有待于提升，通常情况下后者在训练初最常见。二，特征值有正有负，此时模型很可能陷入了鞍点，若陷入鞍点，模型性能表现就很差。以上两种情况在训练初期以及中期，此时若仍然以固定的学习率，会使模型陷入左右来回的震荡或者鞍点，无法继续优化。所以，学习率衰减或者增大能帮助模型有效的减少震荡或者逃离鞍点。

14.3.3 学习率调整策略有哪些？

通常情况下，大部分学习率调整策略都是衰减学习率，当然也有部分增大学习率的策略。这里结合TensorFlow的内置方法来举例。

1、exponential_decay和natural_exp_decay

exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None) natural_exp_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)

指数衰减是最常用的衰减方式，这种方式简单直接，在训练初期衰减较大利于收敛，在后期衰减较小利于精调。以上两种均为指数衰减，区别在于后者使用以自然指数下降。

 

2、piecewise_constant

piecewise_constant(x, boundaries, values, name=None)

分段设置学习率法，跟指数型类似，区别在于每个阶段的衰减并不是按指数调整。可在不同阶段设置手动不同的学习率。这种学习率重点在有利于精调。

3、polynomial_decay

polynomial_decay(learning_rate, global_step, decay_steps, end_learning_rate=0.0001, power=1.0, cycle=False, name=None)

多项式衰减，计算如下：

global_step = min(global_step,decay_steps)

decayed_learning_rate = (learning_rate-end_learning_rate)*(1-global_step/decay_steps)^ (power)+end_learning_rate

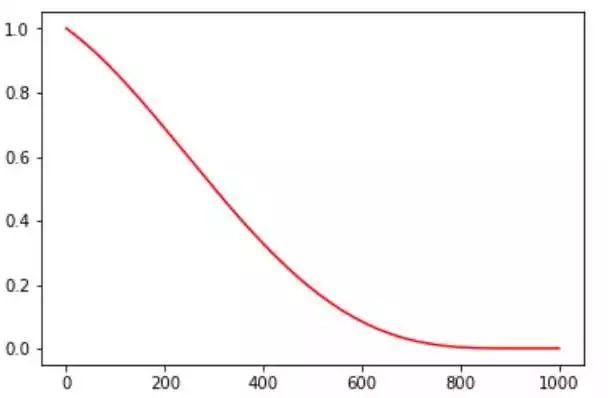
有别去上述两种，多项式衰减则是在每一步迭代上都会调整学习率。主要看Power参数，若Power为1，则是下图中的红色直线；若power小于1，则是开1/power次方，为蓝色线；绿色线为指数，power大于1。

此外，需要注意的是参数cycle，cycle对应的是一种周期循环调整的方式，主要的目的在后期防止在一个局部极小值震荡，若跳出该区域或许能得到更有的结果。这里说明cycle的方式不止可以在多项式中应用，可配合类似的周期函数进行衰减，如下图。

4、inverse_time_decay

inverse_time_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)

逆时衰减，这种方式和指数型类似。如图，

5、cosine_decay

cosine_decay(learning_rate, global_step, decay_steps, alpha=0.0, name=None)

余弦衰减，即按余弦函数的方式衰减学习率，如图

 

6、cosine_decay_restarts

cosine_decay_restarts(learning_rate, global_step, first_decay_steps, t_mul=2.0, m_mul=1.0, alpha=0.0, name=None)

余弦重启衰减，即余弦版本的cycle策略，作用与多项式衰减中的cycle相同。区别在于余弦重启衰减会重新回到初始学习率，拉长周期，而多项式版本则会逐周期衰减。

7、linear_cosine_decay

linear_cosine_decay(learning_rate, global_step, decay_steps, num_periods=0.5, alpha=0.0, beta=0.001, name=None)

线性余弦衰减，主要应用于增强学习领域。

8、noisy_linear_cosine_decay

噪声线性余弦衰减，即在线性余弦衰减中加入随机噪声，增大寻优的随机性。

14.3.4 极端批样本数量下，如何训练网络？

14.3.5 为什么卷积核设计尺寸都是奇数

主要原因有两点：

• 保证像素点中心位置，避免位置信息偏移
• 填充边缘时能保证两边都能填充，原矩阵依然对称

14.3.6 权重共享的形式有哪些，为什么要权重共享

权重共享的形式：

• 深度学习中，权重共享最具代表性的就是卷积网络的卷积操作。卷积相比于全连接神经网络参数大大减少；
• 多任务网络中，通常为了降低每个任务的计算量，会共享一个骨干网络。
• 一些相同尺度下的结构化递归网络

权重共享的好处：

​ 权重共享一定程度上能增强参数之间的联系，获得更好的共性特征。同时很大程度上降低了网络的参数，节省计算量和计算所需内存（当然，结构化递归并不节省计算量）。此外权重共享能起到很好正则的作用。正则化的目的是为了降低模型复杂度，防止过拟合，而权重共享则正好降低了模型的参数和复杂度。

​ 因此一个设计优秀的权重共享方式，在降低计算量的同时，通常会较独享网络有更好的效果。

14.4 合理使用预训练网络

14.4.1 什么是微调（fine-tune）

​ 微调（fine-tune），顾名思义指稍微调整参数即可得到优秀的性能，是迁移学习的一种实现方式。微调和从头训练（train from scratch）的本质区别在于模型参数的初始化，train from scratch通常指对网络各类参数进行随机初始化（当然随机初始化也存在一定技巧），随机初始化模型通常不具有任何预测能力，通常需要大量的数据或者特定域的数据进行从零开始的训练，这样需要训练到优秀的模型通常是稍困难的。而微调的网络，网络各类参数已经在其他数据集（例如ImageNet数据集）完成较好调整的，具备了较优秀的表达能力。因此，我们只需要以较小的学习速率在自己所需的数据集领域进行学习即可得到较为优秀的模型。微调通常情况下，无须再重新设计网络结构，预训练模型提供了优秀的结构，只需稍微修改部分层即可。在小数据集上，通常微调的效果比从头训练要好很多，原因在于数据量较小的前提下，训练更多参数容易导致过度拟合。

14.4.2 微调有哪些不同方法？

​ 以图像分类为例，通常情况下由于不同数据集需要的类别数不同，我们需要修改网络的输出顶层。这种情况下有两种微调方式：

• 不冻结网络模型的任何层，对最后的改动层使用较大的学习率，对未改动层以较小的学习率进行训练全模型训练，进行多轮训练即可。即一步完成训练。

• 冻结除了顶部改动层以外的所有层参数，即不对冻结部分的层进行参数训练更新，进行若干轮的微调训练后，放开顶部层以下的若干层或者全部放开所有层的参数，再次进行若干轮训练即可。即分多步训练。

  以上两种都属于微调。目前由于存在大量优秀的预训练模型，如何确定哪个模型适合自己的任务并能得到最佳性能需要花大量的时间探索。此时，上述的前者是种不错训练方式，你无须进行过多分步的操作。而当探索到一个比较适合的模型时，你不妨可以再次重新尝试下以第二种方式进行训练，或许能得到相比于前者稍高些的性能，因为小数据集上调整过多的参数过拟合的机率也会增大，当然这并不是绝对的。

14.4.3 微调先冻结底层，训练顶层的原因？

​ 14.12中第二种冻结多步训练的方式。首先冻结除了顶部改动层以外的所有层参数，对顶层进行训练，这个过程可以理解为顶层的域适应训练，主要用来训练适应模型的现有特征空间，防止顶层糟糕的初始化，对已经具备一定表达能力的层的干扰和破坏，影响最终的性能。之后，在很多深度学习框架教程中会使用放开顶层往下一半的层数，继续进行微调。这样的好处在于越底层的特征通常是越通用的特征，越往上其整体的高层次语义越完备，这通过感受野很容易理解。所以，若预训练模型的数据和微调训练的数据语义差异越大（例如ImageNet的预模型用于医学图像的训练），那越往顶层的特征语义差异就越大，因此通常也需要进行相应的调整。

14.4.4 不同的数据集特性下如何微调？

• 数据集数据量少，数据和原数据集类似。这是通常做法只需修改最后的输出层，训练即可，训练过多参数容易过拟合。
• 数据集数据量少，数据和原数据集差异较大。由于数据差异较大，可以在完成输出顶层的微调后，微调顶层往下一半的层数，进行微调。
• 数据集数据量大，数据与原数据集差异较大。这种情况下，通常已经不需要用预训练模型进行微调，通常直接重新训练即可。
• 数据集数据量大，数据与原数据类似。这时预训练模型的参数是个很好的初始化，可利用预训练模型放开所有层以较小的学习率微调即可。

14.4.4 目标检测中使用预训练模型的优劣？

​ 目标检测中无论是一阶段的YOLO、SSD或者RetinaNet 还是二阶段的Faster R-CNN、R-FCN 和 FPN都是基于ImageNet上预训练好的分类模型。

​ 优势在于：

​ 1、正如大部分微调的情况一样，使用预训练网络已拥有优秀的语义特征，能有效的加快训练速度；

​ 2、其次，对于大部分二阶段的模型来说，并未实现严格意义上的完全端对端的训练，所以使用预训练模型能直接提取到语义特征，能使两个阶段的网络更容易实现模型的优化。

​ 劣势在于，分类模型和检测模型之间仍然存在一定任务上的差异：

​ 1、检测模型能在多尺度上获取更高的收益；

​ 2、分类模型大部分训练于单目标数据，对同时进行多目标的捕捉能力稍弱；

​ 3、分类模型并不关注目标的位置，在一定程度上让模型损失部分空间信息，这对检测模型通常是不利的。

14.4.5 目标检测中如何从零开始训练？

​ 参考14.15提到的使用预训练模型训练检测模型的优劣势，有两个方案在实际实现中可能会更有效。

​ 方案一、通常二阶段检测模型并未实现真正完全端对端的训练，因此二阶段模型会更难以训练。所以一阶段检测模型相较起来更适合从零训练，参考DSOD，使用DenseNet使用更多层次的特征将更适应训练。

​ 方案二、二阶段模型从零训练很难，而分类模型对于多目标、尺度并不敏感。因此仍然需要预训练模型的参数，这时借鉴DetNet训练一个专属于目标检测的模型网络，而参考分类模型的劣势，该专属网络应对多目标、尺度和位置拥有更强的适应性。

14.5 如何改善 GAN 的性能

优化GAN性能通常需要在如下几个方面进行

• 设计或选择更适合目的代价函数。
• 添加额外的惩罚。
• 避免判别器过度自信和生成器过度拟合。
• 更好的优化模型的方法。
• 添加标签明确优化目标。

GAN常用训练技巧

• 输入规范化到（-1，1）之间，最后一层的激活函数使用tanh（BEGAN除外）

• 使用wassertein GAN的损失函数，

• 如果有标签数据的话，尽量使用标签，也有人提出使用反转标签效果很好，另外使用标签平滑，单边标签平滑或者双边标签平滑

• 使用mini-batch norm， 如果不用batch norm 可以使用instance norm 或者weight norm

• 避免使用RELU和pooling层，减少稀疏梯度的可能性，可以使用leakrelu激活函数

• 优化器尽量选择ADAM，学习率不要设置太大，初始1e-4可以参考，另外可以随着训练进行不断缩小学习率，

• 给D的网络层增加高斯噪声，相当于是一种正则

  14.6 AutoML

14.6.1 什么是AutoML？

​ 目前一个优秀的机器学习和深度学习模型，离不开这几个方面：

​ 一、优秀的数据预处理；

​ 二、合适的模型结构和功能；

​ 三、优秀的训练策略和超参数；

​ 四、合适的后处理操作；

​ 五、严格的结果分析。

​ 这几方面都对最终的结果有着举足轻重的影响，这也是目前的数据工程师和学者们的主要工作。但由于这每一方面都十分繁琐，尤其是在构建模型和训练模型上。而大部分情况下，这些工作有无须过深专业知识就能使用起来。所以AutoML主要的作用就是来帮助实现高效的模型构建和超参数调整。例如深度学习网络的架构搜索、超参数的重要性分析等等。当然AutoML并不简单的进行暴力或者随机的搜索，其仍然需要机器学习方面的知识，例如贝叶斯优化、强化学习、元学习以及迁移学习等等。目前也有些不错的AutoML工具包，例如Alex Honchar的Hyperopt、微软的NNI、Autokeras等。

14.6.2 自动化超参数搜索方法有哪些？

​ 目前自动化搜索主要包含网格搜索，随机搜索，基于模型的超参优化

​ 网格搜索：

​ 通常当超参数量较少的时候，可以使用网格搜索法。即列出每个超参数的大致候选集合。利用这些集合 进行逐项组合优化。在条件允许的情况下，重复进行网格搜索会当优秀，当然每次重复需要根据上一步得到的最优参数组合，进行进一步的细粒度的调整。网格搜索最大的问题就在于计算时间会随着超参数的数量指数级的增长。

​ 随机搜索：

​ 随机搜索，是一种用来替代网格搜索的搜索方式。随机搜索有别于网格搜索的一点在于，我们不需要设定一个离散的超参数集合，而是对每个超参数定义一个分布函数来生成随机超参数。随机搜索相比于网格搜索在一些不敏感超参上拥有明显优势。例如网格搜索对于批样本数量（batch size），在[16,32,64]这些范围内进行逐项调试，这样的调试显然收益更低下。当然随机搜索也可以进行细粒度范围内的重复的搜索优化。

 

​ 基于模型的超参优化：

​ 有别于上述两种的搜索策略，基于模型的超参调优问题转化为了优化问题。直觉上会考虑是否进行一个可导建模，然后利用梯度下降进行优化。但不幸的是我们的超参数通常情况下是离散的，而且其计算代价依旧很高。

​ 基于模型的搜索算法，最常见的就是贝叶斯超参优化。有别于的网格搜索和随机搜索独立于前几次搜索结果的搜索，贝叶斯则是利用历史的搜索结果进行优化搜索。其主要有四部分组成，1.目标函数，大部分情况下就是模型验证集上的损失。2、搜索空间，即各类待搜索的超参数。3、优化策略，建立的概率模型和选择超参数的方式。4、历史的搜索结果。首先对搜索空间进行一个先验性的假设猜想，即假设一种选择超参的方式，然后不断的优化更新概率模型，最终的目标是找到验证集上误差最小的一组超参数。

14.6.3 什么是神经网络架构搜索（NAS）

2015至2017年间，是CNN网络设计最兴盛的阶段，大多都是由学者人工设计的网络结构。这个过程通常会很繁琐。其主要原因在于对不同模块组件的组成通常是个黑盒优化的问题，此外，在不同结构超参数以及训练超参数的选择优化上非凸优化问题，或者是个混合优化问题，既有离散空间又有连续空间。NAS（Neural Architecture Search）的出现就是为了解决如何通过机器策略和自动化的方式设计出优秀高效的网络。而这种策略通常不是统一的标准，不同的网络结合实际的需求通常会有不同的设计，比如移动端的模型会在效率和精度之间做平衡。目前的网络架构搜索通常会分为三个方面，搜索空间，搜索策略以及评价预估。链接 | PaperWeekly

• 搜索空间，定义了优化问题的变量，网络结构和超参数的变量定义有所不同，不同的变量规模对于算法的难度来说也不尽相同。早期很多工作都是用以遗传算法为代表的进化算法对神经网络的超参数和权重进行优化，因为当时的神经网络只有几层，每层十几个神经元，也不存在复杂的网络架构，参数很有限，可直接进行优化。而深度学习模型一方面有着复杂的网络结构，另一方面权重参数通常都以百万到亿来计，进化算法根本无法优化。但换个思路，假如我们找到了一组网络架构参数和对应的超参数，深度学习模型的性能其实是由这组参数来控制和决定的，所以只需要对复杂模型的架构参数和对应的超参数进行优化即可。

• 搜索策略， 搜索策略定义了使用怎样的算法可以快速、准确找到最优的网络结构参数配置。常见的搜索方法包括：随机搜索、贝叶斯优化、进化算法、强化学习、基于梯度的算法。其中，2017 年谷歌大脑的那篇强化学习搜索方法将这一研究带成了研究热点，后来 Uber、Sentient、OpenAI、Deepmind 等公司和研究机构用进化算法对这一问题进行了研究，这个 task 算是进化算法一大热点应用。

• 评价预估，类似于工程优化中的代理模型（surrogate model），因为深度学习模型的效果非常依赖于训练数据的规模，大规模数据上的模型训练会非常耗时，对优化结果的评价将会非常耗时，所以需要一些手段去做近似的评估。

  一种思路是用一些低保真的训练集来训练模型，低保真在实际应用可以有多种表达，比如训练更少的次数，用原始训练数据的一部分，低分辨率的图片，每一层用更少的滤波器等。用这种低保真的训练集来测试优化算法会大大降低计算时间，但也存在一定的 bias，不过选择最优的架构并不需要绝对数值，只需要有相对值就可以进行排序选优了；

  另一种主流思路是借鉴于工程优化中的代理模型，在很多工程优化问题中，每一次优化得到的结果需要经过实验或者高保真仿真（有限元分析）进行评价，实验和仿真的时间非常久，不可能无限制地进行评价尝试，学者们提出了一种叫做代理模型的回归模型，用观测到的点进行插值预测，这类方法中最重要的是在大搜索空间中如何选择尽量少的点预测出最优结果的位置；

  第三种主流思路是参数级别的迁移，用之前已经训练好的模型权重参数对target问题进行赋值，从一个高起点的初值开始寻优将会大大地提高效率。在这类问题中，积累了大量的历史寻优数据，对新问题的寻优将会起到很大的帮助，用迁移学习进行求解，是一个很不错的思路；另一种比较有意思的思路叫做单次（One-Shot）架构搜索，这种方法将所有架构视作一个 one-shot 模型（超图）的子图，子图之间通过超图的边来共享权重。