图像对齐：MeshFlow: Minimum Latency Online Video Stabilization

MeshFlow: Minimum Latency Online Video Stabilization

FAST Features

作者引用《Fast Corner Detection》中的角点检测算法，分别检测参考帧、畸变帧的特征点。检测方式如下：
1.以像素点$p$为中心，取半径为3的Bresenham圆上的16个连续的像素点，如果这16个连续的像素点中有$n$个连续的像素点的像素值都大于$I(p)+t$，或者都小于$I(p)-t$，则像素点$p$为FAST特征点的候选点，一般$n$取12，$t$为阈值
2.计算得到像素点$p$与像素点1、5、9、13之间的像素值差异，如果至少有3个像素点与$p$间的差值绝对值大于阈值$t$，则像素点$p$依旧为FAST特征点
3.一般情况下，为了加速计算，可以先计算第二步，满足第二步的情况下，再计算第一步

FAST特征点检测示意图

Track by KLT

作者引用Takeo Kanade 的论文《An Iterative Image Registration Technique with an Application to Stereo Vision》当中对特征点的跟踪算法，但这篇论文本身论证得比较清楚的是一维数据的匹配问题和相邻两帧之间只有平移变换的匹配问题，任意特征点的匹配在作者CMU的课程报告《Detection and Tracking of Point Features》中有更详细的介绍，为了清晰，下面的关于KLT的内容，一维数据的匹配问题采用《An Iterative Image Registration Technique with an Application to Stereo Vision》中的论述，用于描述作者所提供的方法的物理依据，二维图像的匹配问题采用《Detection and Tracking of Point Features》中的论述，方便厘清如何实现二维图像数据的匹配，另外《Detection and Tracking of Point Features》这篇Report写得比较长，如果想要简单了解KLT的导出过程，也可以阅读Stan Birchfield写的《Derivation of Kanade-Lucas-Tomasi Tracking Equation 》一文。

1D Case

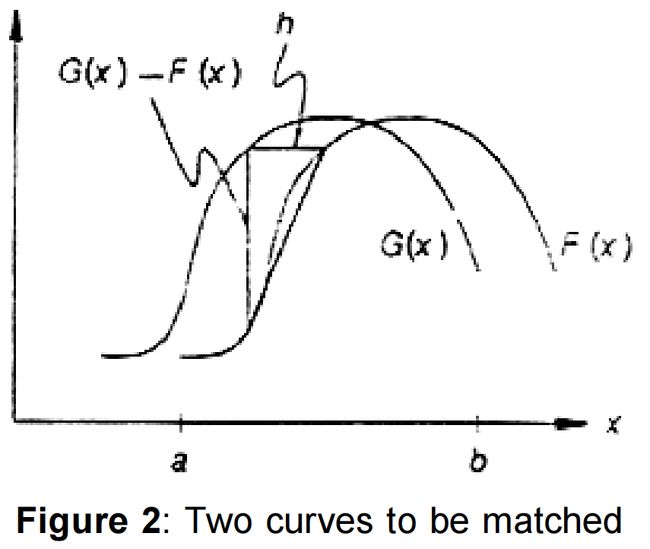
对于一维数据的特征点匹配问题，如下图所示，希望能够找到$G(x)、F(x)$间的位移$h$，如果$h$足够小，对$F(x)$在点$x$处做线性近似：
$$F^{{}^{\prime }}\approx \frac{F(x+h)-F(x)}{h}=\frac{G(x)-F(x)}{h}\text{\hspace{1em}(a.1)}$$
即：
$$h\approx \frac{G(x)-F(x)}{F^{{}^{\prime }}(x)}\text{\hspace{1em}(a.2)}$$
通过组合不同的$x$来达到对$h$的平滑的目的：
$$h\approx \frac{{\sum }_x\frac{G(x)-F(x)}{F^{’}(x)}}{{\sum }_{x}1}\text{\hspace{1em}(a.3)}$$
在下图中，存在相交的两个点，$G(x)-F(x)=0$，但$G^{{}^{\prime }}、F^{{}^{\prime }}$间的差异很大，可以用$\frac{1}{|G^{{}^{\prime }}-F^{{}^{\prime }}|}$替换掉上面的权重系数1，即位移$h$变为：
$$h\approx \frac{{\sum }_{x}w(x)\frac{G(x)-F(x)}{F^{’}(x)}}{{\sum }_{x}w(x)}；w(x)=\frac{1}{|G^{{}^{\prime }}-F^{{}^{\prime }}|}\text{\hspace{1em}(a.4)}$$
向$h$所示方向移动$F(x)$，并逐步迭代，直至$F(x)、G(x)$间的差值小于某阈值$T$时，认为找到了曲线$F(x)$相对于$G(x)$的位移，即完成了一维数据点$x$在这两条曲线上的匹配，迭代过程如下:
$$\begin{gathered} h_0=0 \\ {h}_{k+1}=h_k+\frac{{\sum }_{x}w(x)\frac{G(x)-F(x)}{F^{’}(x)}}{{\sum }_{x}w(x)}\text{\hspace{1em}(a.5)} \end{gathered}$$

2D Case

针对二维图像的特征点匹配问题，KLT做了一个基本的假设，认为相邻帧当中检测处理的相互匹配的特征点，在以其为中心的某个尺寸的Window当中，Window内的点的像素值相差不大，即是:$I(x,y,t+\tau )=I(x-\xi ,y-\eta ,t)$，其中$t+\tau$表示下一帧，$t$表示当前帧，$\mathbf{d}=(\xi ,\eta )$为对应特征点$\mathbf{x}=(x,y)$在下一帧中的位移。因此，可以同通过最小化特征点在前、后帧中对应Window当中的像素值差值来进行特征点匹配。重新定义$J(\mathbf{x})=I(x,y,t+\tau )$为当前帧的特征点，$I(\mathbf{x}-\mathbf{d})=I(x-\xi ,y-\eta ,t)$对应下一帧的特征点，有$J(\mathbf{x})=I(\mathbf{x}-\mathbf{d})+n(\mathbf{x})$，其中$n$表示噪声，通过最小化特征点在其Window内的残差来求解位移向量$\mathbf{d}$：
$$ϵ={\int }_{\mathcal{W}}[I(\mathbf{x}-\mathbf{d})-J(\mathbf{x}){]}^{2}wd\mathbf{x}\text{\hspace{1em}(a.6)}$$
其中$\mathcal{W}$为Window，$w$为权重函数，常用1或高斯函数。对图像$I$的亮度信息进行一阶泰勒展开：
$$I(\mathbf{x}-\mathbf{d})=I(\mathbf{x})-\mathbf{g}\cdot \mathbf{d}\text{\hspace{1em}(a.7)}$$
其中$\mathbf{g}$为一阶导，重写式(a.6)，得：
$$ϵ={\int }_{\mathcal{W}}[I(\mathbf{x})-\mathbf{g}\cdot \mathbf{d}-J(\mathbf{x}){]}^{2}wd\mathbf{x}={\int }_{\mathcal{W}}(h-\mathbf{g}\cdot \mathbf{d}{)}^{2}wd\mathbf{x}\text{\hspace{1em}(a.8)}$$
其中$h=I(\mathbf{x})-J\mathbf{x}$。上式是关于$\mathbf{d}$的二次函数，通过令导数为0进行求解：
$${\int }_{\mathcal{W}}(h-\mathbf{g}\cdot \mathbf{d})\mathbf{g}wdA=0\text{\hspace{1em}(a.9)}$$
由于假设Window内的$\mathbf{d}$是恒定的，且$(\mathbf{g}\cdot \mathbf{d})\mathbf{g}=\left(\mathbf{g}{\mathbf{g}}^T\right)\mathbf{d}$，即是：
$$\left({\int }_{\mathcal{W}}{\mathbf{g}\mathbf{g}}^{T}wdA\right)\mathbf{d}={\int }_{\mathcal{W}}h\mathbf{g}wdA\text{\hspace{1em}(a.10)}$$
即是：
$$G\mathbf{d}=\mathbf{e}\text{\hspace{1em}(a.11)}$$
其中系数矩阵$G={\int }_{\mathcal{W}}{\mathbf{g}\mathbf{g}}^{T}wdA$，是一个$2\times 2$的对称阵；$\mathbf{e}={\int }_{\mathcal{W}}(I-J)\mathbf{g}wdA$是一个二维向量。求解方程(a.11)即可解的位移$\mathbf{d}$，逐步迭代直至帧差$\mathbf{e}$小于设定阈值$T$时，认为追踪到角点。

RANSAC

Ransac的原文是《Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography》，下面的内容总结自Milan Sonka的《Image Processing, Analysis, and Machine Vision》一书。
相机位姿变化导致的图像畸变一般的线性的，一般可以通过最小二乘法最小化残差平方和来拟合匹配过后的特征点之间的线性关系。当数据存在某种噪声时，一般性的做法是将数据中相对于拟合模型的残差最大的一些数据点当做异常值，排除这些异常值后重新计算模型，但这种做法做了有关数据本身相关性的假设，这种假设可能并不成立，这是由于误差有典型的两类：
1.测量误差：对应于特征点匹配当中由运动物体带来的特征点本身的移动
2.分类误差：对应于特征点匹配当中的错配
最小二乘建立在使用尽可能多的数据能带来有益的平滑效果的假设基础上的，但这种假设针对特征点匹配的异常点的检出并不是合适的选择，更合适的选择是通过随机抽样一致来拟合。在拟合直线时，两个点就能够定义一条直线，可以在数据集中随机选取两个点并假设连接这两个点的直线就是正确的模型，可以计算在某种程度上接近假设的直线的数据点，称为一致点(Consensus Points)的数目来测试此模型，如果大部分点都是一致点，可以利用一致点集重新拟合得到一个更好的模型，而不是剔除异常值。
1.假设要将$n$个数据点$X=x_1....x_n$拟合为一个由至少$m$个点决定的模型，$m\le n$

2.设迭代次数$k=1$，给定偏差$ϵ$

3.从$X$中随机选取$m$个项并拟合模型

4.计算$X$中相对于模型的残差在偏差$ϵ$内的元素个数，如果元素个数大于阈值$t$，根据一致点集重新拟合模型，可以利用最小二乘或其变形，终止算法

5.$k=k+1$，如果$k$小于一个事先给定的$K$，跳至3，否则采用具有最大一致点集的模型，或者算法失败

MeanFlow

Motion Propagation

完成相邻两帧图像间特征点的检测及匹配之后，根据每对特征点$p,\hat{p}$的坐标差异，计算运动向量$v_p=p-\hat{p}$，将图像划分为$16\times 16$的均匀网格，每个运动向量传播至以其自身所在网格为中心的$3\times 3$的网格内

Median Filters

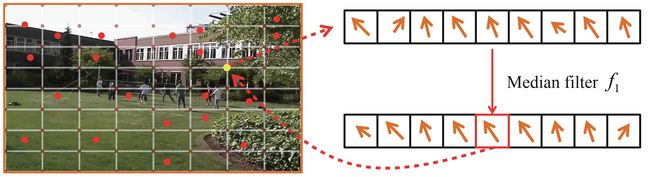
如下图每个网格顶点都将受到其邻域内的多个运动向量的影响，对这些运动向量做一个中值滤波，得到一个更平滑的运动场

但如下图所示，中值滤波$f_1$不能滤除网格中比较大的离群点，因此，作者建议再使用一个$3\times 3$的中值滤波，来去除这些离群点，产生更加平滑的运动场

中值滤波是光流法中的常规操作，但是在本文作者引用的中值滤波的论文《Secrets of Optical Flow Estimation and Their Principles》中有提到两次中值滤波会导致光流法性能的下降。

Vertex Profiles Generation

通过记录每个网格顶点在整个视频图像序列中的运动向量，生成对应顶点的运动轮廓

Robust Estimation

1.Rich Features：在进行特征点检测的时候，一般需要设置一个全局的阈值对特征响应值进行筛选，会造成图像的纹理区域检测到的特征点过少甚至没有，因此在特征点的检测过程中，可以根据网格分块，设置局部阈值，避免部分网格内检测不到合适数量特征点的问题。

2.Outlier Rejection：将图像分成$4\times 4$的子图，并用RANSAC去除每个子图中因错误匹配、物体运动而造成的离群点

3.Pre-warping：在MehFlow之前，用全部匹配后的特征点计算出一个全局的单应性矩阵$F_t$，$F_t$用以表征全图的运动向量$V_t$，并用$F_t$对$\hat{p}$的坐标进行预矫正，即该点的局部运动向量为${\tilde{v}}_p=p-F_t\tilde{p}$，该点的全部运动向量为$v_p=V_t+{\tilde{v}}_p$，一些少特征点区域的网格顶点将只受全局运动向量的影响

Predicted Adaptive Path Smoothing

为了在视频后期或者实时处理视频的时候，产生类似于物理防抖(比如陀螺仪)的视频稳定效果，需要在时域上对MeshFlow计算出来的运动向量或者说Warping Map做一个约束，使得展示给视频观看者的视频拥有较好的平滑性。

Offline Adaptive Smoothing

首先，将之前记录下来的每个网格顶点的在整个视频序列中的运动向量看作是一个局部地相机运动路径$C_i$，单帧所用网格顶点的运动向量之和看作时整体的相机运动路径$C$。期望通过约束相机运动路径的相似性来得到优化后的相机路径$P$：
$$\mathcal{O}(\mathbf{P}(t))=\sum _t\left(\Vert \mathbf{P}(t)-\mathbf{C}(t){\Vert }^2+{\lambda }_t\sum _{r\in {\Omega }_t}{w}_{t,r}\Vert \mathbf{P}(t)-\mathbf{P}(r){\Vert }^2\right)\text{\hspace{1em}(1)}$$
其中$C(t)={\sum }_t\mathbf{v}(t)$表示$t$时刻的相机路径，$\mathbf{v}(t)$表示$t$时刻的MeshFlow，${\Omega }_t$表示以$t$时刻在时域上的平滑半径$r$，$w_{t,r}=e^{-\frac{||r-t|{|}^2}{\frac{{\Omega }_t}{3}}}$为影响权重，${\lambda }_t$为两项间的平衡参数，因此，上式的第一项用于约束经平滑后的运动向量$P$与原运动向量$C$之间的相似性，上式的第二项是约束当前帧$t$与其半径为$r$的时域范围的经优化的运动向量将的相似性，是本方法中的平滑项，上式通过Jacobin迭代求解。

Predict ${\lambda }_t$

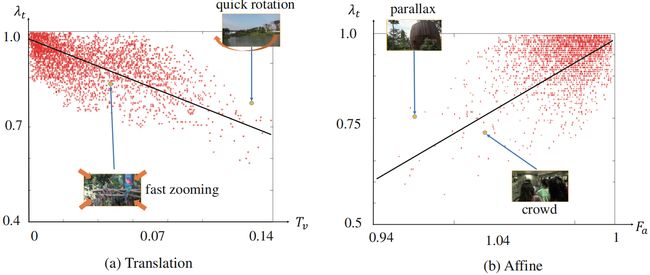
根据当前帧相机的运动来自适应一个合适的参数${\lambda }_t$，作者用到了两个经验性的指标：
Translational element $T_v$：$T_v=\sqrt{v_x^2+v_y^2}$，其中$v_x、v_y$对应前面计算出来的全局性的单应性矩阵$F$中的平移分量
Affine component $F_a$：单应性矩阵$F$的仿射变换部分的两个最大特征值的比值
下图为50个快速移动的摄像机拍摄视频计算出来的参数${\lambda }_t$和$T_v、F_a$之间的关系(没有明白的是这些数据对应的${\lambda }_t$是哪里来的)，并用这些数据拟合了两个线性模型，如下：
$$\begin{array}{c}{\lambda }_t^{\prime }=-1.93\times T_v+0.95\\ {\lambda }_t^{\prime \prime }=5.83\times F_a+4.88\\ {\lambda }_t=max(min({\lambda }_t^{’},{\lambda }_t^{{}^{\prime \prime }}),0)\end{array}$$

Online Smoothing

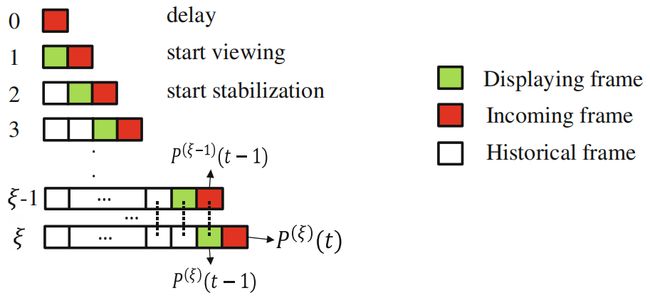
在线视频稳定相比前面的稳定离线视频的问题的区别主要集中在一下几个方面：①要求速度实时；②只能使用过去帧，不能使用下一帧；③需要在buffer内缓存一定帧数。下图是本文所提在线视频稳定算法的基本框架，当相机开始采集第零帧时，由于没参考帧，第零帧不做稳定处理，且延迟一帧播放，当相机采集第一帧时，用缓存的前一帧数据计算相机运动向量，但此运动向量不作用于图像，直接播放第一帧图像，当相机采集第三帧数据时，计算运动向量，并根据式(1)的约束，计算用于视频稳定的运动向量$P_t$，播放稳定后的第二帧。

buffer内需要缓存大约1s的历史数据，并且在式(1)中添加历史
$$\mathcal{O}\left({\mathbf{P}}^{(\xi )}(t)\right)=\sum _{t\in \Phi }\left({\Vert {\mathbf{P}}^{(\xi )}(t)-\mathbf{C}(t)\Vert }^2+{\lambda }_t\sum _{t\in \Phi ,r\in {\Omega }_t}{w}_{t,r}{\Vert {\mathbf{P}}^{(\xi )}(t)-{\mathbf{P}}^{(\xi )}(r)\Vert }^2\right)+\beta \sum _{t\in \Phi }{\Vert {\mathbf{P}}^{(\xi )}(t-1)-{\mathbf{P}}^{(\xi -1)}(t-1)\Vert }^2\text{\hspace{1em}(2)}$$
与(1)不同的是上式的$\Phi$表示的式buffer中缓存的数据；其中参数$\xi$表示第$\xi$次优化。上式第一项用于约束当前帧$P$经平滑后的运动向量$P$与原运动向量$C$之间的相似性；第二项用于约束当前帧$P$与buffer内缓存的历史帧间的相似性；第三项用于约束当前播放帧在第$\xi$次对$P$的优化过程的结果和第$\xi -1$次对$P$的优化过程的结果间的相似性。