pytorch 一个最简单的回归预测

回归预测其实就是根据数据找出对应的拟合函数，假设我们需要拟合的函数为，也就是给一个x，可以输出一个x^2。

第一步产生训练数据与对应标签：

生成的训练数据只有一个特征值，每一个数据代表一个样本，因此要扩充一下维度。另外本来标签应该是直接对应label=x.pow(2)，但是考虑到真实数据可能没法一一对应，因此加入一定噪声干扰，当然不加噪声干扰也是可以的。

# 样本
x = torch.linspace(-5, 5, 100)
x = torch.unsqueeze(x, dim=1)  

# 标签
noise = np.random.uniform(-5,5,x.size())
noise = torch.from_numpy(noise)
label = x.pow(2)+0.2*noise 

第二步搭建网络：

每次网络进行输入的时候都是一个值，因此全连接层的输入层为1，设置隐藏层为10个，输出层为1，因为一个x对应的label也是一个值。在前向传播的时候经过每一个隐藏层后都需要进行激活，最后输出层不用激活。

class Net_R(nn.Module):
    def __init__(self):
        super(Net_R, self).__init__()
        self.hidden = nn.Linear(1, 10)
        self.pre = nn.Linear(10, 1)

    def forward(self, x):
        x = self.hidden(x)
        x = torch.relu(x)
        x = self.pre(x)
        return x

第三步开始训练：

训练步骤很简单，首先选定网络，优化器和损失函数这三个。然后就开始训练，这里一共训练200个周期。

每个周期训练的时候步骤为：

1、将数据送入网络进行预测pre = net(data)

2、训练得到的值与真实的标签值送入到Loss函数进行损失的求解loss = loss_func(pre,label)

3、先将前一次的梯度值清空，然后根据当前损失进行方向传播loss.backward()

4、传播后对梯度进行更新optimizer.step()

5、模型保存，在对模型进行保存的时候要判断，当前在训练集的准确度时候高于上一次的准确度，如果当前准确度比上一次高才进行更新保存，否则不保存当前训练的参数.这里由于我们用的损失函数是MSELoss，那么其实loss这个参数就能表示我们预测的准确度，因此只需要比较哪个epoch的loss小

def train():
    best_loss = float('inf')
    net = Net_R()
    optimizer = torch.optim.Adam(net.parameters(), lr=0.1)
    loss_func = nn.MSELoss()
    for t in range(1, 201):
        pre = net(data)
        loss = loss_func(pre, label)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if(best_loss>loss):
            best_loss = loss
            torch.save(net, 'net.pkl')          # 保存整个网络
            # torch.save(net.'state_dict()')    # 只保存参数
        

第四步加载模型进行测试：

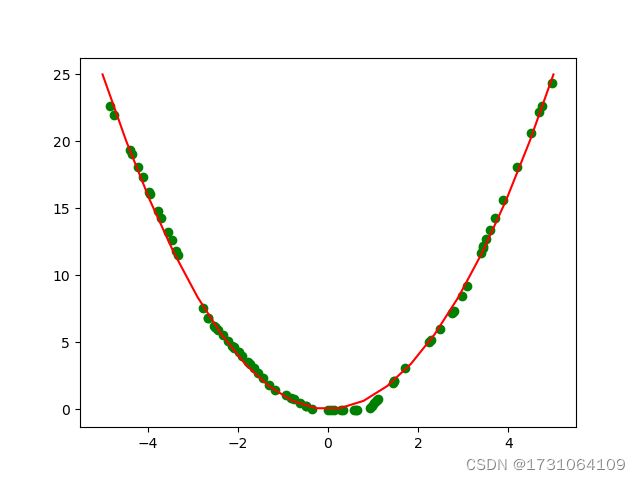
先生成测试数据，可以跟生成训练数据一样生成测试数据，也可以随机生成，这里为了展示模型的拟合效果，测试数据采用随机生成的方式。将测试结果绘制出来，代码中的x1,y用于绘制二次曲线函数，便于观测测试效果。

def test_R():
    x1 = torch.linspace(-5, 5, 20)       # 这里的数据不用于检测，仅用于绘图
    x1 = torch.unsqueeze(x1, dim=1)      # dim=1在行上面加维度
    y = x1.pow(2)

    x = np.random.uniform(-5,5,(80,1))    # 生成待测试数据
    x = torch.from_numpy(x)
    net = torch.load('Regression.pkl')
    with torch.no_grad():
        out = net(x)
        plt.figure()
        plt.plot(x1,y,c='r')
        plt.scatter(x,out,c='g')
        plt.show()