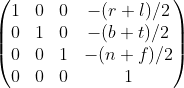GAMES101 作业1(附旋转矩阵和投影矩阵推导)

目录

第一题

第二题

---

第一题

题目: 返回一个绕 z 轴旋转给定转动角度(rotation_angle)的旋转矩阵。

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    return model;
}

解析:

        这道题比较简单, 但有一个坑, 就是 rotation_angle 是角度, 需要将其转化为弧度, 也就是令rotation_angle = rotation_angle * PI / 180。

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    rotation_angle = rotation_angle / 180 * MY_PI;
    model << cos(rotation_angle), -sin(rotation_angle), 0, 0,
        sin(rotation_angle), cos(rotation_angle), 0, 0,
        0, 0, 1, 0,
        0, 0, 0, 1;
    return model;
}

        个人觉得这个旋转矩阵的推导从基变换的角度理解比较好记: 

        首先提取出旋转矩阵的第一列(cos(rotation_angle), sin(rotation_angle), 0, 0)T, 代码中是逆时针旋转的矩阵。可以想象一下，将基向量(1, 0, 0)T 绕 Z 轴逆时针旋转 rotation_angle°，由简单的三角函数推导，可以得到结果 (cos(rotation_angle), sin(rotation_angle), 0)T。同理可证得第二列。

---

第二题

题目: 给定视场角(eye_fov), 宽高比(aspect_ratio), 近平面位置(zNear), 远平面位置(zFar), 

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.
    return projection;
}

解析:

 1. 构造正交投影矩阵:

        正交投影矩阵的作用就是将给定的空间中的长方体映射在一个的立方体中。因此首先需要做的就是将物体先平移再缩放, 而平移就是将长方体从它的中心移到原点。设长方体的边界为b(bottom), t(top), l(left), r(right), n(near), f(far), 可以得到平移矩阵:

以及放缩矩阵:

放缩矩阵右乘平移矩阵就可以得到正交投影矩阵:

。

2. 构造“压缩”矩阵：

        这一步时为了通过将物体在远平面上的投影压缩到透视投影后的状态，再进行正交投影，使得透视投影操作变得更加简单。

         我们期待的是：假设原平面上有齐次坐标，则在近平面上的齐次坐标根据相似三角形原理可得 , 又因为是齐次坐标，故同乘 z 后表示的坐标不变，可将其变换为 。由此可以推得 中的部分元素:

(A, B, C, D为未知数), 由近平面(near)上的点在经过投影变换后不变, 可以设近平面上一点坐标, 为了利用已经获得的部分元素, 将坐标乘以n, 得, 因此有 A*x + B*y + C*n + D = n² , 由此可得 A = B = 0 , 则 C*n + D = n² 。再由远平面(far)上的中点不变, 可得, 可变换为, 同上, 有  A*x + B*y + C*f + D = f² , 已知 A = B = 0 , 则 C*f + D = f² 。联立 C*n + D = n² 与 C*f + D = f² , 最终得到:

3. 代码:

       投影矩阵为 , 只要用代码实现即可:

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.

    eye_fov = eye_fov / 180 * MY_PI;        //将角度转为弧度
    float top = zNear * tan(eye_fov * 0.5); //需要变换的长方体的顶部
    float bottom = -top;                    //需要变换的长方体的底部
    float right = top * aspect_ratio;       //需要变换的长方体的右侧
    float left = -right;                    //需要变换的长方体的左侧

    Eigen::Matrix4f ortho = Eigen::Matrix4f::Identity();    //Mortho
    ortho <<    2 / (right - left), 0, 0, (right + left) / (right - left),
                0, 2 / (top - bottom), 0, (top + bottom) / (top - bottom),    //此处应将2 / (top - bottom) 改为 2 / (bottom - top), 因为投影视图是上下颠倒的
                0, 0, 2 / (zNear - zFar), (zFar + zNear) / (zFar - zNear),
                0, 0, 0, 1;

    Eigen::Matrix4f squish = Eigen::Matrix4f::Identity();   //Msquish->ortho
    squish <<   zNear, 0, 0, 0,
                0, zNear, 0, 0,
                0, 0, zNear + zFar, -zNear * zFar,
                0, 0, 1, 0;

    projection = ortho * squish;
    return projection;
}