Python 各种画图

说实话，Python 画图和 Matlab 画图十分相似『Matlab 转战 Python』—— 沃兹·基硕德

Part.I 基础知识

Chap.I 快应用

• Python 常用线型 + 点符号 + 颜色汇总
• Python 中图例 Legend 的调整
• Python 修改 x/y ticks
• Python 绘图字体与位置控制

---

下面是『进阶使用』：

• Python 让多图排版更加美观
• Python 箱型图的绘制并提取特征值

Chap.II 常用语句

下面是一些基本的绘图语句：

import matplotlib.pyplot as plt			# 导入模块

plt.style.use('ggplot')					# 设置图形的显示风格
fig=plt.figure(1)						# 新建一个 figure1
fig=plt.figure(figsize=(12,6.5),dpi=100,facecolor='w')
fig.patch.set_alpha(0.5)				# 设置透明度为 0.5
font1 = {'weight' : 60, 'size' : 10}	# 创建字体，设置字体粗细和大小
ax1.set_xlim(0,100)						# 设置 x 轴最大最小刻度
ax1.set_ylim(-0.1,0.1)					# 设置 y 轴最大最小刻度
plt.xlim(0,100)  						# 和上面效果一样
plt.ylim(-1,1)
ax1.set_xlabel('X name',font1)			# 设置 x 轴名字
ax1.set_ylabel('Y name',font1)			# 设置 y 轴名字
plt.xlabel('aaaaa')						# 设置 x 轴名字
plt.ylabel('aaaaa')						# 设置 y 轴名字
plt.grid(True)					 		# 增加格网
plt.grid(axis="y")						# 只显示横向格网
plt.grid(axis="x")						# 只显示纵向格网
ax=plt.gca()							# 获取当前axis,
fig=plt.gcf()							# 获取当前figures
plt.gca().set_aspect(1)					# 设置横纵坐标单位长度相等
plt.text(x,y,string)					# 在 x,y 处加入文字注释
plt.gca().set_xticklabels(labels, rotation=30, fontsize=16) # 指定在刻度上显示的内容
plt.xticks(ticks, labels, rotation=30, fontsize=15)   # 上面两句合起来
plt.legend(['Float'],ncol=1,prop=font1,frameon=False)	# 设置图例 列数、去掉边框、更改图例字体
plt.title('This is a Title')			# 图片标题
plt.show()								# 显示图片，没这行看不见图
plt.savefig(path, dpi=600)				# 保存图片，dpi可控制图片清晰度
plt.rcParams['font.sans-serif'] = ['SimHei']  	# 添加这条可以让图形显示中文
mpl.rcParams['axes.unicode_minus'] = False		# 添加这条可以让图形显示负号
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')				#设置图片的右边框和上边框为不显示
# 子图
ax1=plt.subplot(3,1,1)
ax1.scatter(time,data[:,1],s=5,color='blue',marker='o') # size, color, 标记
ax1=plt.subplot(3,1,2)
...
# 控制图片边缘的大小
plt.subplots_adjust(left=0, bottom=0, right=1, top=1，hspace=0.1,wspace=0.1)

# 设置坐标刻度朝向，暂未成功
plt.rcParams['xtick.direction'] = 'in'
ax = plt.gca()
ax.invert_xaxis() 
ax.invert_yaxis()

Part.II 画图样例

不要忘记 import plt

import matplotlib.pyplot as plt

下面是一些简单的绘图示例，上面快应用『进阶使用』部分会有些比较复杂的操作，感兴趣的可参看。

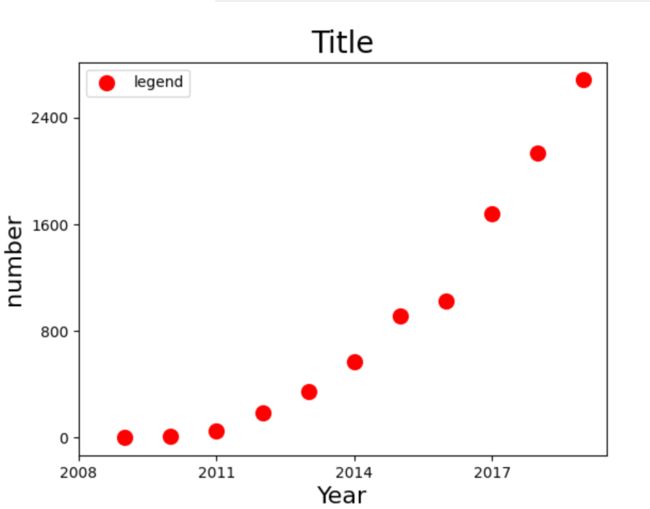
Chap.I 散点图

years = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
turnovers = [0.5, 9.36, 52, 191, 350, 571, 912, 1027, 1682, 2135, 2684]
plt.figure()
plt.scatter(years, turnovers, c='red', s=100, label='legend')
plt.xticks(range(2008, 2020, 3))
plt.yticks(range(0, 3200, 800))
plt.xlabel("Year", fontdict={'size': 16})
plt.ylabel("number", fontdict={'size': 16})
plt.title("Title", fontdict={'size': 20})
plt.legend(loc='best')
plt.show()

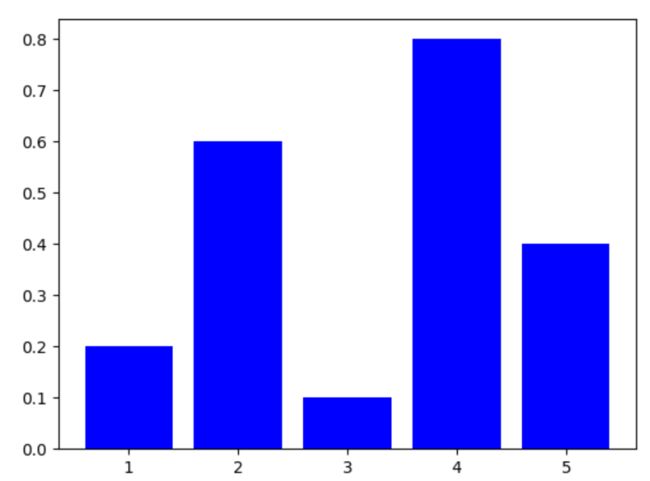
Chap.II 柱状图

X=[1,2,3,4,5]
Y=[0.2,0.6,0.1,0.8,0.4]
plt.bar(X,Y,color='b')
plt.show()

Chap.III 折线图

参考：https://blog.csdn.net/AXIMI/article/details/99308004

plt.rcParams['font.sans-serif'] = ['SimHei']  # 添加这条可以让图形显示中文
x_axis_data = [1, 2, 3, 4, 5]
y_axis_data = [1, 2, 3, 4, 5]
# plot中参数的含义分别是横轴值，纵轴值，线的形状，颜色，透明度,线的宽度和标签
plt.plot(x_axis_data, y_axis_data, 'ro-', color='#4169E1', alpha=0.8, linewidth=1, label='一些数字')
# 显示标签，如果不加这句，即使在plot中加了label='一些数字'的参数，最终还是不会显示标签
plt.legend(loc="upper right")
plt.xlabel('x轴数字')
plt.ylabel('y轴数字')
plt.show()

Chap.IV 概率分布直方图

主要通过函数plt.hist()来实现，

matplotlib.pyplot.hist(  
x, bins=10, range=None, normed=False,edgecolor='k',   
weights=None, cumulative=False, bottom=None,   
histtype=u'bar', align=u'mid', orientation=u'vertical',   
rwidth=None, log=False, color=None, label=None, stacked=False,   
hold=None, **kwargs)

其中，常用的参数及其含义如下：

• bins：“直方条”的个数，一般可取20
• range=(a,b)：只考虑区间(a,b)之间的数据，绘图的时候也只绘制区间之内的
• edgecolor=‘k’：给直方图加上黑色边界，不然看起来很难看（下面的例子就没加，所以很难看）

example_list=[]
n=10000
for i in range(n):
    tmp=[np.random.normal()]
    example_list.extend(tmp)
width=100
n, bins, patches = plt.hist(example_list,bins = width,color='blue',alpha=0.5)
X = bins[0:width]+(bins[1]-bins[0])/2.0
Y = n
maxn=max(n)
maxn1=int(maxn%8+maxn+8*2)
ydata=list(range(0,maxn1+1,maxn1//8))
yfreq=[str(i/sum(n)) for i in ydata]
plt.plot(X,Y,color='green')     #利用返回值来绘制区间中点连线
p1 = np.polyfit(X, Y, 7)        #利用7次多项式拟合，返回拟多项式系数，按照阶数从高到低排列
Y1 = np.polyval(p1,X)
plt.plot(X,Y1,color='red')
plt.xlim(-2.5,2.5)	
plt.ylim(0)
plt.yticks(ydata,yfreq)        #这条语句控制纵坐标是频数或频率，打开是频率，否则是频数
plt.legend(['midpoint','fitting'],ncol=1,frameon=False)
plt.show()

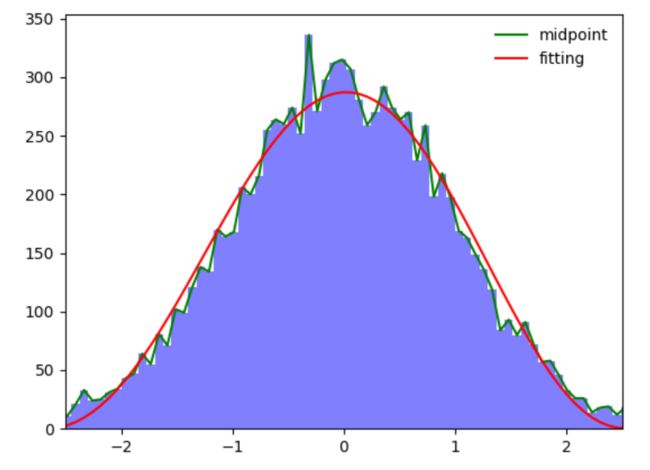
上面的图片中，绿线是直方图矩形的中点连线，红线是根据直方图的中点7次拟合的曲线。

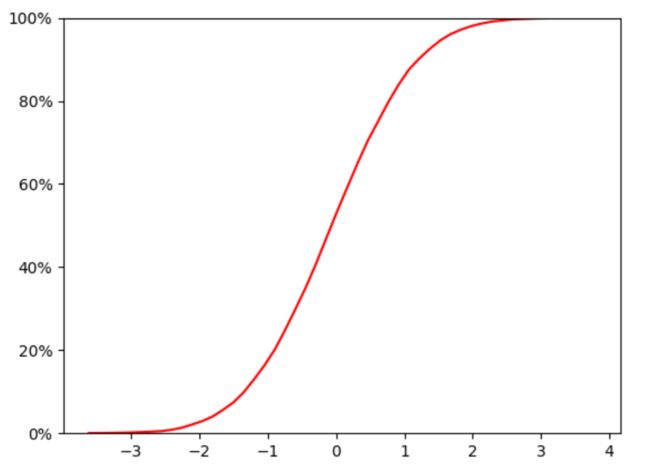
Chap.V 累计概率分布曲线

累积分布函数(Cumulative Distribution Function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。

example_list=[]
n=10000
for i in range(n):
    tmp=[np.random.normal()]
    example_list.extend(tmp)
width=50
n, bins, patches = plt.hist(example_list,bins = width,color='blue',alpha=0.5)
plt.clf()           # clear the figure
X = bins[0:width]+(bins[1]-bins[0])/2.0
bins=bins.tolist()
freq=[f/sum(n) for f in n]
acc_freq=[]
for i in range(0,len(freq)):
    if i==0:
        temp=freq[0]
    else:
        temp=sum(freq[:i+1])
    acc_freq.append(temp)
plt.plot(X,acc_freq,color='r')                    # Cumulative probability curve
yt=plt.yticks()
yt1=yt[0].tolist()
def to_percent(temp,position=0):          # convert float number to percent
    return '%1.0f'%(100*temp) + '%'
ytk1=[to_percent(i) for i in yt1 ]
plt.yticks(yt1,ytk1)
plt.ylim(0,1)
plt.show()

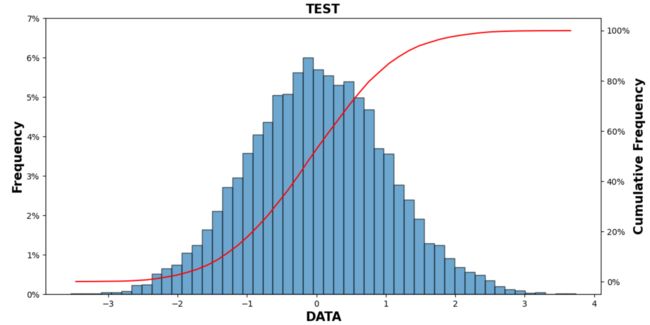
Chap.VI 概率分布直方图+累计概率分布图

参考：https://blog.csdn.net/qq_38412868/article/details/105319818
可以绘制概率分布直方图和累计概率曲线

笔者进行了一些的改编：

def draw_cum_prob_curve(data,bins=20,title='Distribution Of Errors',xlabel='The Error(mm)',pic_path=''):
    """
    plot Probability distribution histogram and Cumulative probability curve.
    
    > @param[in] data:          The error data
    > @param[in] bins:          The number of hist
    > @param[in] title:         The titile of the figure
    > @param[in] xlabel:        The xlable name
    > @param[in] pic_path:      The path where you want to save the figure
    return:     void
    """
    import matplotlib.pyplot as plt
    import matplotlib as mpl
    from matplotlib.ticker import FuncFormatter
    from matplotlib.pyplot import MultipleLocator
    def to_percent(temp,position=0):          # convert float number to percent
        return '%1.0f'%(100*temp) + '%'
    fig, ax1 = plt.subplots(1, 1, figsize=(12, 6), dpi=100, facecolor='w')
    font1 = {'weight': 600, 'size': 15}
    
    n, bins, patches=ax1.hist(data,bins =bins, alpha = 0.65,edgecolor='k') # Probability distribution histogram
    yt=plt.yticks()
    yt1=yt[0].tolist()
    yt2=[i/sum(n) for i in yt1]
    ytk1=[to_percent(i) for i in yt2 ]
    plt.yticks(yt1,ytk1)
    X=bins[0:-1]+(bins[1]-bins[0])/2.0 
    bins=bins.tolist()
    freq=[f/sum(n) for f in n]
    acc_freq=[]
    for i in range(0,len(freq)):
        if i==0:
            temp=freq[0]
        else:
            temp=sum(freq[:i+1])
        acc_freq.append(temp)
    ax2=ax1.twinx()                         # double ylable
    ax2.plot(X,acc_freq)                    # Cumulative probability curve
    ax2.yaxis.set_major_formatter(FuncFormatter(to_percent))
    ax1.set_xlabel(xlabel,font1)
    ax1.set_title(title,font1)
    ax1.set_ylabel('Frequency',font1)
    ax2.set_ylabel("Cumulative Frequency",font1)
    #plt.savefig(pic_path,format='png', dpi=300)

调用示例：

example_list=[]
n=10000
for i in range(n):
    tmp=[np.random.normal()]
    example_list.extend(tmp)
tit='TEST'
xla='DATA'
draw_cum_prob_curve(example_list,50,tit,xla)
plt.show()