计算机视觉中评价指标计算:Accuracy,Precision,Recall,AP,mAP,Top-1,Top-5,Top-N ranked,IoU
计算机视觉中评价指标计算:Accuracy,Precision,Recall,AP,mAP,Top-1,Top-5,Top-N ranked,IoU
- 引言
- 对应场景
-
- 图像分类(image classification)
- 目标检测(object detection)
- 指标计算
-
- 准确率(Accuracy),精确度(Precision),召回率(Recall)
- 在image classification中
- 在object detection中
-
- 一个例子
- AP in PASCAL VOC challenge
- mAP
- 参考
引言
CV论文中会涉及到其性能评价的指标,刚开始以为用一个精度(accuracy)就可以表示了,但随着阅读增多,发现了不同的评价指标,并且在不同的视觉任务中,指标需求不一样。同时,有些指标计算相对复杂,不深入了解很难记住。为此,花了点时间查阅了一些资料,在此整理一下。
对应场景
不同的指标对应的场景不同,如果没有弄清这一点,在查阅资料过程中,会容易产生:
- “为什么会有这个?”
- “这个又是怎么计算的?”
- “为什么这样可以?”
等疑问,初学者容易犯这个错误。
因此,在明白怎么计算之前,一定要明确当前的使用场景,是图像分类(image classification)还是目标检测(object detection),具体可以参考该网址,其分成了四类,classification,classification+location,object detection和instance segmentation,但主要以以下两种作为视觉图像的基本任务。
图像分类(image classification)
给定一张图片,判断为其是属于哪个类别,即输入网络一张图片,网络输出其属于某个类别的概率。一般而言:
- 对于二分类任务,输出一个2维向量,表示属于该类和不属于该类的概率(如0.9的概率为狗,0.1的概率不为狗);
- 对于N分类(N>2),输出一个N维向量,表示该图像为各N类的概率(如0.5的概率为狗,0.3的概率为猫,0.1的概率为牛,……)。
CNN经典的网络,如AlexNet,VGG,GoogLeNet,ResNet专门用于图像分类任务,现在已作为其他视觉任务(不仅仅是上述提出的4种场景)的基本网络(baseline)。
在图像分类任务中,用的最多的是Top-1和Top-5 error rate,而Top-1和Top-5 error rate也只用于图像分类(注意与Top-N ranked区别,两者没有关系)
|
|
目标检测(object detection)
给定一张图片,框出其中每个对象的位置,并判断该对象是属于哪类,即输入网络一张图片,网络输出M个边界框(bounding box)的位置(x,y,h,w),同时每个边界框包含一个置信度C(confidence) 和一个N类别的概率信息P,表示在该图像中的M个地方检测到了疑似目标,每个位置的可信度为C(M个位置也就是C1,C2,……,CM),其属于N类的概率分别为P1,P2,……,PN。简言之,输出一个M×(4+1+N)维向量,其中M不定,因为图片中到底有多少个目标是未知的。
在目标检测任务中,一般用AP,mAP作为评价指标。
|
|
指标计算
通常而言,无论是哪一种视觉检测任务,总可以用预测正确和错误两种结果评估,分类正确/错误,检测正确/错误,分割正确/错误,只是说在不同的任务中判断标准不同,比如:
- image classification中可以根据输出的类别概率中最高概率类别和输入图像的label作比较;
- object detection中可以根据输出bounding box的参数(x,y,h,w,C,P)和ground truth作比较(下文会给出详细说明)。
准确率(Accuracy),精确度(Precision),召回率(Recall)
对于判断正确/错误,就引出了准确率(Accuracy),精确度(Precision),召回率(Recall)三个概念,需要注意的是这三个概念并没有特定的使用场景限定,先理解这三个词和其含义。
在实际检测任务中,判断结果会存在4种情况:
样本是正的,预测结果也是正的,即将正样本检测出来了,正确的正样本,用True Positive(TP)表示;样本是正的,预测结果是负的,即将正样本当作了负的,错误的负样本,用False Negative(FN)表示;样本是负的,预测结果也是负的,即将负样本检测出来了,正确的负样本,用True Negative(TN)表示;样本是负的,预测结果是正的,即将负样本当作了正的,错误的正样本,用False Positive(FP)表示。
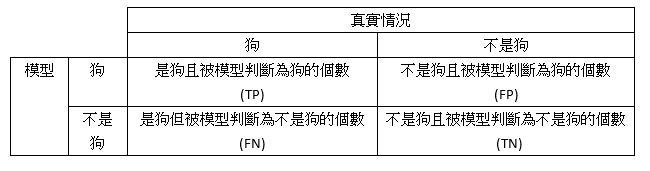 图3 图3
|
以一个判断图片是否为狗的任务为例,TP表示能够检测出狗,FN表示图片是狗但没检测出来,TN表示图片不是狗检测结果也不是狗,FP则表示图片不是狗但检测结果是狗。
显然,TP和TN是正确的判断结果,FN和FP是错误的判断结果,因此可以用预测正确的样本数占整个样本数的比例来评价检测器性能,即:
Y = T P + T N T P + F N + F P + T N Y=\frac{TP+TN}{TP+FN+FP+TN} Y=TP+FN+FP+TNTP+TN
这就是准确性(Accuracy)的计算方法,即:
A c c u r a c y = T P + T N T P + F N + F P + T N Accuracy=\frac{TP+TN}{TP+FN+FP+TN} Accuracy=TP+FN+FP+TNTP+TN
在正负样本分布均匀的情况中,Accuracy能够较好地反映检测指标,但在分布不均匀的样本中Accuracy指标存在缺陷,比如有一个由90张狗的正样本图片和10张非狗的负样本图片组成的数据集,若分类器将所有图片全判断为狗,也能取得90%的Accuracy指标,这显然是不合理的。为此,引出了精确度(Precision)和召回率(Recall)的评价指标:
Precision表示所有预测为正的样本中,真实正样本所占的比例
如预测为狗的图像中,确实为狗的比例,计算方法为:
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
Recall表示所有的正样本中,预测为正的样本的比例
如在样本里所有为狗的图像集合中,有多大比例狗图像被正确预测出来了,计算方法为:
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
在image classification中
网络的输出为一个C维向量(该图片属于各类的概率值),将其各元素按照降序排列,最大值所对应的label即为该图片的分类结果。按照上述Precision和Recall的定义可以求出每个类别的分类指标(当作C个二分类任务),但实际中,由于image classification任务强调的是样本集的总体分类性能,一般用分类错误率来评估,即样本集中有多大比例的样本被分错了类别。
因此,用Top-1和Top-5 error rate指标来评价分类性能,其差别在于分类正确或错误的标准不同
e r r o r r a t e = 分 类 错 误 的 样 本 数 样 本 集 数 量 error\ rate=\frac{分类错误的样本数}{样本集数量} error rate=样本集数量分类错误的样本数
Top-1 error rate:将输出的C维向量按照降序排列,如果最大值所对应label与ground truth label不符,则该图片属于分类错误,最后用分类错误的样本数量除以样本集的数量得到Top-1 error rate;
Top-5 error rate:将输出的C维向量按照降序排列,如果前5个对应的label没有包含ground truth label,则该图片属于分类错误,最后用分类错误的样本数量除以样本集的数量得到Top-5 error rate;
显然,Top-1 error rate标准比Top-5 error rate要严格。
在object detection中
相比于image classification,object detection的评估指标计算要复杂一些,除了需要计算bounding box的位置误差外,还需计算每个bounding box对应的类别概率。为此,在object detection中,一般用AP(average precision)和mAP(mean average precision)两个指标评估。
上文已述,object detection的输出为一个M×(4+1+N)维向量,其中,M表示输出bounding box的个数(由于一个图片存在多少个object是未知的,因而M值未定),4为bounding box的位置信息(x,y,w,h),1表示该bounding box的置信度(即多大概率是一个object),N为该object属于各个类别的概率(类似image classification的输出),而ground truth为一个L×(4+1)维向量,其中L为bounding box的个数(注意:与M没有关系),4个位置信息(x,y,w,h),1个object标签。
置信度决定了预测bounding box是否包含一个object的可能性,检测中会产生数量远大于ground truth的bounding box,为此在计算指标前会剔除置信度低于某个值的bounding box,比如0.5。
不同于image classification中的样本集error rate整体评价指标,object detection强调的是每一个类别的检测指标,比如狗的检测AP、汽车的检测AP、人的检测AP等。
此外,由于预测bounding box的数量M是一个非确定值,在计算指标时,并不是以样本集的数量为基准,而是以这个样本集中预测的有效bounding box总体数量为准(注意不是M,因为有一部分的置信度太低需要剔除)。
AP,average precision,平均精确度,比上文precision多了一个average,显然计算AP时有一个求平均的过程。在上文precision和recall的介绍中,两者是存在一定关系的,当调整算法的阈值提高recall时,precision会降低,反之,precision会提高,通俗的说就是提高recall可以让检测出来的样本更多的预测为正样本(减少FN),但这样会让一些负样本也预测为正样本(FP增高),导致precision降低。通过多次调整阈值,可以获得不同recall下的precision,最后累加这些precision求平均便得到了average precision。
下面举一个例子进一步介绍AP计算过程,该例子参考该网址。
一个例子
在一个object detection任务中,需要求狗的检测AP,真实情况是样本中有8只狗(GT1-GT8),而总共预测出了10只狗(BB1-BB10,注意剔除了置信度较低的bounding box)。
预测的bounding box和ground truth bounding box之间的关系用IoU表示,IoU(Intersection over Union,交并比),指的是预测的bounding box和ground truth bounding box之间的交集和并集的面积比值,当两者完全重合时,IoU为100%,没有任何交集时为0,显然IoU值越大,模型预测的bounding box性能越好。
 图4 IoU计算 图4 IoU计算
|
图5所示为统计的数据,由于有些BB只检测到了狗的部分,如头或脚,所以IoU很低(BB3,BB4,BB5,BB7,BB8),然后有些狗未检测到(GT7,GT8,属于FN)。
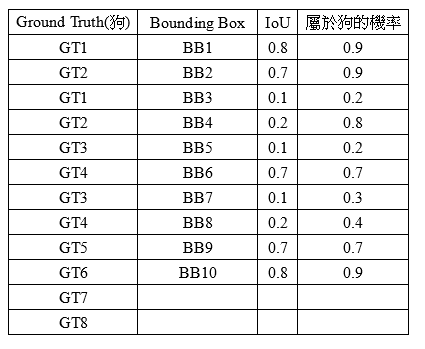 图5 图5
|
假设判断一个BB是否预测正确的标准为IoU≥0.5,则可以获得图6所示的结果,其中:
TP=(BB1,BB2,BB6,BB9,BB10)
FP=(BB3,BB4,BB5,BB7,BB8)
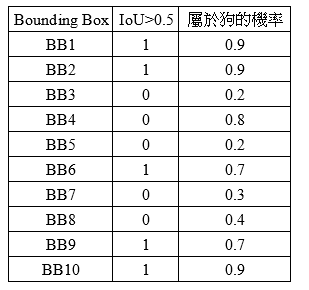 图6 图6
|
然后按照预测为各类object概率中狗的概率对图6排序,得到图7:
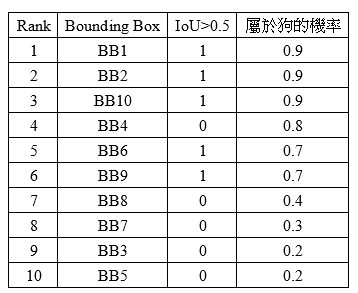 图7 图7
|
接着,根据不同的rank计算precision和recall,这里就涉及到了Top-N ranked
Top-N ranked指的对排序后的样本统计数据按照前n个样本划分N次rank,分别求出每次rank后的precision和recall,直至n=N,N为预测的总数量。
Rank 1:
P r e c i s i o n = rank 1 预 测 为 狗 的 数 量 rank 1 总 预 测 数 = 1 1 = 1 R e c a l l = rank 1 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 1 8 = 0.125 Precision =\frac {\text{rank 1}预测为狗的数量} {\text{rank 1}总预测数}=\frac{1}{1}=1\\\text{}\\ Recall = \frac{\text{rank 1}预测为狗的数量 }{样本集中狗的总数}=\frac{1}{8}=0.125 Precision=rank 1总预测数rank 1预测为狗的数量=11=1Recall=样本集中狗的总数rank 1预测为狗的数量=81=0.125
Rank 2:
P r e c i s i o n = rank 2 预 测 为 狗 的 数 量 rank 2 总 预 测 数 = 2 2 = 1 R e c a l l = rank 2 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 2 8 = 0.25 Precision =\frac {\text{rank 2}预测为狗的数量} {\text{rank 2}总预测数}=\frac{2}{2}=1\\\text{}\\ Recall = \frac{\text{rank 2}预测为狗的数量 }{样本集中狗的总数}=\frac{2}{8}=0.25 Precision=rank 2总预测数rank 2预测为狗的数量=22=1Recall=样本集中狗的总数rank 2预测为狗的数量=82=0.25
Rank 3:
P r e c i s i o n = rank 3 预 测 为 狗 的 数 量 rank 3 总 预 测 数 = 3 3 = 1 R e c a l l = rank 3 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 3 8 = 0.375 Precision =\frac {\text{rank 3}预测为狗的数量} {\text{rank 3}总预测数}=\frac{3}{3}=1\\\text{}\\ Recall = \frac{\text{rank 3}预测为狗的数量 }{样本集中狗的总数}=\frac{3}{8}=0.375 Precision=rank 3总预测数rank 3预测为狗的数量=33=1Recall=样本集中狗的总数rank 3预测为狗的数量=83=0.375
Rank 4:
P r e c i s i o n = rank 4 预 测 为 狗 的 数 量 rank 4 总 预 测 数 = 3 4 = 0.75 R e c a l l = rank 4 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 3 8 = 0.375 Precision =\frac {\text{rank 4}预测为狗的数量} {\text{rank 4}总预测数}=\frac{3}{4}=0.75\\\text{}\\ Recall = \frac{\text{rank 4}预测为狗的数量 }{样本集中狗的总数}=\frac{3}{8}=0.375 Precision=rank 4总预测数rank 4预测为狗的数量=43=0.75Recall=样本集中狗的总数rank 4预测为狗的数量=83=0.375
Rank 5:
P r e c i s i o n = rank 5 预 测 为 狗 的 数 量 rank 5 总 预 测 数 = 4 5 = 0.8 R e c a l l = rank 5 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 4 8 = 0.5 Precision =\frac {\text{rank 5}预测为狗的数量} {\text{rank 5}总预测数}=\frac{4}{5}=0.8\\\text{}\\ Recall = \frac{\text{rank 5}预测为狗的数量 }{样本集中狗的总数}=\frac{4}{8}=0.5 Precision=rank 5总预测数rank 5预测为狗的数量=54=0.8Recall=样本集中狗的总数rank 5预测为狗的数量=84=0.5
Rank 6:
P r e c i s i o n = rank 6 预 测 为 狗 的 数 量 rank 6 总 预 测 数 = 5 6 = 0.833 R e c a l l = rank 6 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 5 8 = 0.625 Precision =\frac {\text{rank 6}预测为狗的数量} {\text{rank 6}总预测数}=\frac{5}{6}=0.833\\\text{}\\ Recall = \frac{\text{rank 6}预测为狗的数量 }{样本集中狗的总数}=\frac{5}{8}=0.625 Precision=rank 6总预测数rank 6预测为狗的数量=65=0.833Recall=样本集中狗的总数rank 6预测为狗的数量=85=0.625
Rank 7:
P r e c i s i o n = rank 7 预 测 为 狗 的 数 量 rank 7 总 预 测 数 = 5 7 = 0.714 R e c a l l = rank 7 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 5 8 = 0.625 Precision =\frac {\text{rank 7}预测为狗的数量} {\text{rank 7}总预测数}=\frac{5}{7}=0.714\\\text{}\\ Recall = \frac{\text{rank 7}预测为狗的数量 }{样本集中狗的总数}=\frac{5}{8}=0.625 Precision=rank 7总预测数rank 7预测为狗的数量=75=0.714Recall=样本集中狗的总数rank 7预测为狗的数量=85=0.625
Rank 8:
P r e c i s i o n = rank 8 预 测 为 狗 的 数 量 rank 8 总 预 测 数 = 5 8 = 0.625 R e c a l l = rank 8 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 5 8 = 0.625 Precision =\frac {\text{rank 8}预测为狗的数量} {\text{rank 8}总预测数}=\frac{5}{8}=0.625\\\text{}\\ Recall = \frac{\text{rank 8}预测为狗的数量 }{样本集中狗的总数}=\frac{5}{8}=0.625 Precision=rank 8总预测数rank 8预测为狗的数量=85=0.625Recall=样本集中狗的总数rank 8预测为狗的数量=85=0.625
Rank 9:
P r e c i s i o n = rank 9 预 测 为 狗 的 数 量 rank 9 总 预 测 数 = 5 9 = 0.556 R e c a l l = rank 9 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 5 8 = 0.625 Precision =\frac {\text{rank 9}预测为狗的数量} {\text{rank 9}总预测数}=\frac{5}{9}=0.556\\\text{}\\ Recall = \frac{\text{rank 9}预测为狗的数量 }{样本集中狗的总数}=\frac{5}{8}=0.625 Precision=rank 9总预测数rank 9预测为狗的数量=95=0.556Recall=样本集中狗的总数rank 9预测为狗的数量=85=0.625
Rank 10:
P r e c i s i o n = rank 10 预 测 为 狗 的 数 量 rank 10 总 预 测 数 = 5 10 = 0.5 R e c a l l = rank 10 预 测 为 狗 的 数 量 样 本 集 中 狗 的 总 数 = 5 8 = 0.625 Precision =\frac {\text{rank 10}预测为狗的数量} {\text{rank 10}总预测数}=\frac{5}{10}=0.5\\\text{}\\ Recall = \frac{\text{rank 10}预测为狗的数量 }{样本集中狗的总数}=\frac{5}{8}=0.625 Precision=rank 10总预测数rank 10预测为狗的数量=105=0.5Recall=样本集中狗的总数rank 10预测为狗的数量=85=0.625
图8为统计结果,依此可以画出图9所示的precision-recall曲线:
 图8 图8
|
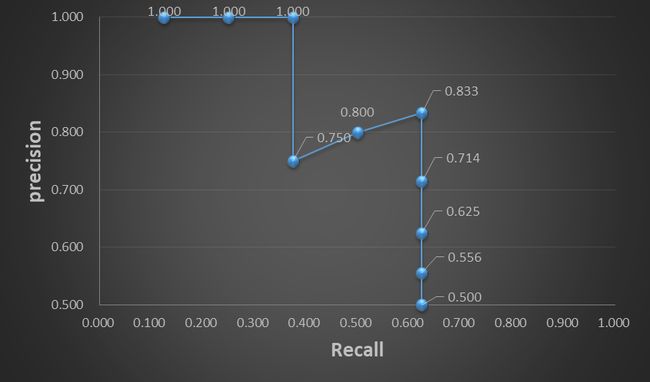 图9 Precision-Recall曲线 图9 Precision-Recall曲线
|
AP就是计算这条precision-recall曲线下的面积(area under curve,AUC)。
AP in PASCAL VOC challenge
VOC 2010之间的方法在计算AP时会做一个变化,选取Recall≥0,0.1,0.2,……,1,这11个Recall值处的Precision的最大值。
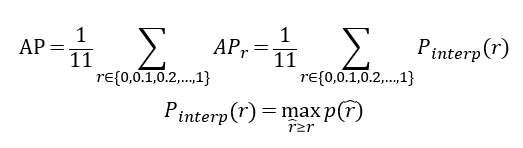 图10 图10
|
其中,p为precision,r={0,0.1,0.2,……,1}
VOC 2010之后对recall的判断值做了修改,选取Recall≥0,0.14,0.29,0.43,0.57,0.71,1,这7个位置的Precision最大值。
 图11 图11
|
据此,按照VOC 2010之前的AP计算可得:
A P 1 = 1 + 1 + 1 + 1 + 0.833 + 0.833 + 0.833 + 0 + 0 + 0 + 0 11 = 6.499 11 = 0.591 AP_1=\frac{1+1+1+1+0.833+0.833+0.833+0+0+0+0}{11}=\frac{6.499}{11}=0.591 AP1=111+1+1+1+0.833+0.833+0.833+0+0+0+0=116.499=0.591
按照VOC 2010之后的AP计算可得:
A P 2 = 1 + 1 + 1 + 0.833 + 0.833 + 0 + 0 7 = 4.666 7 = 0.667 AP_2=\frac{1+1+1+0.833+0.833+0+0}{7}=\frac{4.666}{7}=0.667 AP2=71+1+1+0.833+0.833+0+0=74.666=0.667
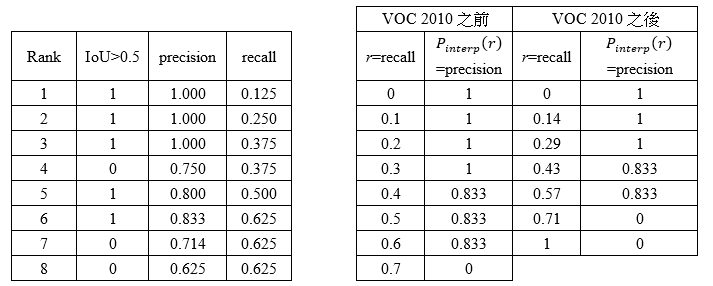 图12 图12
|
| 左边的计算结果是根据不同的rank去计算precision和recall;右边是根据给定的recall值来计算precision |
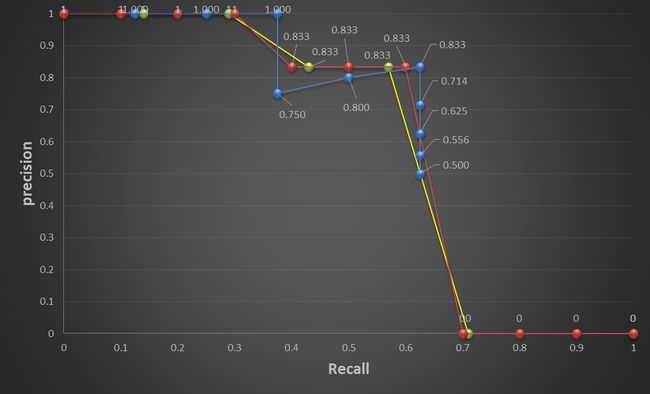 图12 图12
|
| 红色为VOC 2010之前的计算方法,黄色为VOC 2010之后的计算方法 |
此外,在一些论文中会看到AP(0.5,0.05,0.95)的说法,其指的是在评估性能时IoU判断阈值是变化的,一般而言,IoU判断阈值为0.5。
mAP
AP的概念讲完了,mAP就好理解了。AP指的是一个类别的指标(如上文的狗检测例子),而一个object detection任务包含多个类别,如VOC包含20类object,则会计算出20个AP,将其累加取平均便得到mAP。
参考
1.基于深度学习的目标检测技术演进:R-CNN、Fast R-CNN、Faster R-CNN
2.深度學習系列: 什麼是AP/mAP?
3.图3至图12摘抄了Tommy Huang的博文深度學習系列: 什麼是AP/mAP?(若涉嫌版权,烦请告知)