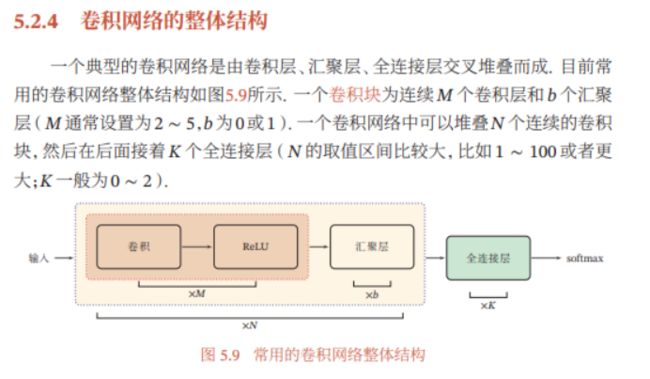
卷积神经网络(CNN)网络结构及模型原理介绍
概述
本篇内容仅介绍卷积层,池化层等网络结构部分和构建原理,以及卷积的一些前提知识。全连接层的内容和分类模型及损失函数的构建优化和全连接神经网络相同,这里不再讲解。
神经网络模型构建及算法介绍:https://blog.csdn.net/stephon_100/article/details/125452961
卷积神经网络是一种深层前馈神经网络.用不同的卷积核对同一个图像进行卷积其实就是用卷积核对图像进行滤波以提取不同的特征。
所以卷积神经网络模型也是自动提取特征的模型,附带分类功能。
假设卷积层的输入神经元个数为M,卷积大小为K,步长为S,在输入两端各 填补P个0,那么该卷积层的神经元数量为(M - K + 2P)/S+1
通常可以通过选择合 适的卷积大小以及步长来使得![]() 为整数.
为整数.
主要内容:
卷积神经网络(Convolutional Neural Network,CNN或ConvNet)是一种 具有局部连接、权重共享等特性的深层前馈神经网络.
卷积神经网络最早主要是用来处理图像信息.在用全连接前馈网络来处理 图像时,会存在以下两个问题:
(1)参数太多:如果输入图像大小为100 × 100 × 3(即图像高度为100,宽 度为 100 以及 RGB 3 个颜色通道),在全连接前馈网络中,第一个隐藏层的每个 神经元到输入层都有 100 × 100 × 3 = 30 000 个互相独立的连接,每个连接都对 应一个权重参数.随着隐藏层神经元数量的增多,参数的规模也会急剧增加.这 会导致整个神经网络的训练效率非常低,也很容易出现过拟合.
(2) 局部不变性特征:自然图像中的物体都具有局部不变性特征,比如尺 度缩放、平移、旋转等操作不影响其语义信息.而全连接前馈网络很难提取这些 局部不变性特征,一般需要进行数据增强来提高性能.
全连接层一般在卷积 网络的最末层. 卷积神经网络有三个结构上的特性:局部连接、权重共享以及汇聚.这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性.和 前馈神经网络相比,卷积神经网络的参数更少.
预备补充知识
卷积的定义 :卷积(Convolution),也叫褶积,是分析数学中一种重要的运算.在信号处 理或图像处理中,经常使用一维或二维卷积
一维卷积:
二维卷积 :
根据卷积定义,上图的计算需要进行卷积核翻转。翻转指从两个维度(从 上到下、从左到右)颠 互相关(Cross-Correlation)是一个 倒次序,即旋转180度。翻转后就可以直接进行点积操作,即对应位置相乘再求和。如图:
在图像处理中常用的均值滤波(Mean Filter)就是一种二维卷积,将当前 位置的像素值设为滤波器窗口中所有像素的平均值,即![]()
直观展示:
在图像处理中,卷积经常作为特征提取的有效方法.一幅图像在经过卷积操 作后得到结果称为特征映射(Feature Map).图5.3给出在图像处理中几种常用 的滤波器,以及其对应的特征映射.图中最上面的滤波器是常用的高斯滤波器, 可以用来对图像进行平滑去噪;中间和最下面的滤波器可以用来提取边缘特征.
因此总结用卷积核对图像进行卷积其实就是用卷积核对图像进行滤波以提取特定的特征。
(3)互相关
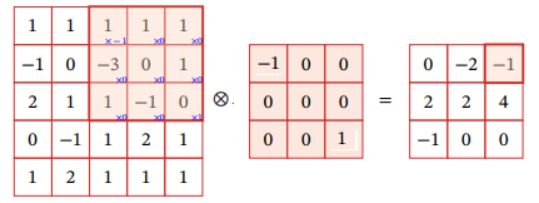
在机器学习和图像处理领域,卷积的主要功能是在一个图像(或某种特征) 上滑动一个卷积核(即滤波器),通过卷积操作得到一组新的特征.在计算卷积 的过程中,需要进行卷积核翻转.在具体实现上,一般会以互相关操作来代替卷 积,从而会减少一些不必要的操作或开销.
互相关(Cross-Correlation)是一个倒次序,即旋转180度. 衡量两个序列相关性的函数,通常是用滑动窗口的点积计算来实现.给定一个图 像![]() 和卷积核
和卷积核![]() ,它们的互相关为:
,它们的互相关为:
和公式 (5.7) 对比可知,互相关和卷积的区别仅仅在于卷积核是否进行翻转.因 此互相关也可以称为不翻转卷积.
卷积和互相关对比(扩展):
可见卷积运算和互相关运算的关系是:
给定一个图 像![]() 和卷积核
和卷积核![]() ,它们的互相关为
,它们的互相关为
和公式 (5.7) 对比可知,互相关和卷积的区别仅仅在于卷积核是否进行翻转.因 此互相关也可以称为不翻转卷积.
因此互相关通常是直接用滑动窗口的点积计算来实现,而不是严格数学上的卷积即将滑动窗口翻转后再求点积。
在神经网络中使用卷积是为了进行特征抽取,卷积核是否进行翻转和其特 征抽取的能力无关.特别是当卷积核是可学习的参数时,卷积和互相关在能力上 是等价的.因此,为了实现上(或描述上)的方便起见,我们用互相关来代替卷 积.事实上,很多深度学习工具中卷积操作其实都是互相关操作.
之后描述中,除 非特别声明,卷积一般 指“互相关”.卷积符号 用⊗来表示,即不翻转 卷积.真正的卷积用 ∗来表示.
在卷积的标准定义基础上,还可以引入卷积核的滑动步长和零填充来增加 卷积的多样性,可以更灵活地进行特征抽取.
步长(Stride)是指卷积核在滑动时每次滑动几个像素点.
零填充(Zero Padding)是在输入向量两端进行补零.
假设卷积层的输入神经元个数为M,卷积大小为K,步长为S,,在输入两端各 填补P个0,那么该卷积层的神经元数量为(M - K + 2P)/S+1
通常可以通过选择合 适的卷积大小以及步长来使得![]() 为整数.
为整数.
卷积神经网络
根据卷积的定义,卷积层有两个很重要的性质:局部连接,权重共享。
以上图为例:
如果是全连接操作,每一个神经元需要连接前面所有的25个输入像素x,也就有25个权重w和1个偏置b.
但如果是卷积操作,整个5x5的图像都只用这一个卷积核窗口来滑动,因此权重参数只需求卷积窗口大小3x3=9个参数和一个偏置参数b,上图就是以步长为1且图像两端不补0来滑动窗口得到的卷积的结果
通常卷积核的大小远远小于被卷积的输入图像的大小,所以卷积操作相比全连接要训练的参数要少很多。
(1)卷积层
卷积层的作用是提取一个输入图片滤波后的图像也即输入图片的一个特征,不同的卷积核相当于不同的特 征提取器.前面讲的内容都是二维图像的卷积。但通常一个彩色图像由多个颜色通道组成,所以一般表示为三维的信息。那么卷积核的神经元也是在三维上卷积的。
通常将三维结构表示为,其大小为高度x宽度x深度,即MxNxD,
在输入层,特征映射就是图像本身.如果是灰度图像,就是有一个特征映射, 输入层的深度D=1,;如果是彩色图像,分别有 RGB 三个颜色通道的特征映射, 输入层的深度D=3。
特征映射(Feature Map)为一幅图像(或其他特征映射)在经过卷积提取 到的特征,每个特征映射可以作为一类抽取的图像特征.为了提高卷积网络的表 示能力,可以在每一层卷积层中堆叠多个不同的的卷积核得到一个图像的多个不同的特征映射,以更好地表示图像的特征.
解释:每一个卷积层包含P个神经元即卷积核,因此经过这一层的卷积就会产生P个特征图。输入的一个图像的大小为MxN的大小,深度为D,如果是彩色图有RGB共3个通道,所以d=3。卷积核的大小为UxV的大小,深度为D。
(2)汇聚层(池化层)
汇聚层(Pooling Layer)也叫子采样层(Subsampling Layer),池化层,其作用是进 行特征选择,降低特征数量,从而减少参数数量,避免过拟合。
(1) 最大汇聚(Maximum Pooling或Max Pooling):对于一个区域选择这个区域内所有神经元的最大活性值作为这个区域的表示
(2) 平均汇聚(Mean Pooling):一般是取区域内所有神经元活性值的平 均值,
汇聚层不但 可以有效地减少神经元的数量,还可以使得网络对一些小的局部形态改变保持 不变性,并拥有更大的感受野.
典型的汇聚层是将每个特征映射划分为2 × 2大小的不重叠区域,然后使用 最大汇聚的方式进行下采样.汇聚层也可以看作一个特殊的卷积层,卷积核大小 为KxK,步长为SxS,卷积核为max函数或 mean函数.过大的采样区域会急 剧减少神经元的数量,也会造成过多的信息损失.