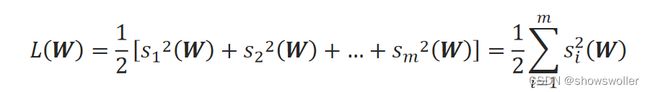【Python机器学习】梯度下降法的讲解和求解方程、线性回归实战（Tensorflow、MindSpore平台 附源码）

需要全部源码请点赞关注收藏后评论区留言私信~~~

基本思想

迭代关系式是迭代法应用时的关键问题，而梯度下降（Gradient Descent）法正是用梯度来建立迭代关系式的迭代法。 机器学习模型的求解一般可以表示为：

其中，f(x)为机器学习模型的损失函数。

也称为无约束最优化模型。

对于无约束最优化问题argmin┬xf(x)，其梯度下降法求解的迭代关系式为：

 

式中，x为多维向量，记为x=(x^(1),x^(2),…,x^(n))；α为正实数，称为步长，也称为学习率；df(x)/dx=(■8(■8(∂f(x)/∂x^(1)&∂f(x)/∂x^(2))&■8(⋯&∂f(x)/∂x^(n))))是f(x)的梯度函数。

 梯度下降法的几个问题：

1）梯度下降法的结束条件，一般采用：①迭代次数达到了最大设定；②损失函数降低幅度低于设定的阈

2）关于步长α，过大时，初期下降的速度很快，但有可能越过最低点，如果“洼地”够大，会再折回并反复振荡。如果步长过小，则收敛的速度会很慢。因此，可以采取先大后小的策略调整步长，具体大小的调节可根据f(x)降低的幅度或者x前进的幅度进行。

3）关于特征归一化问题，梯度下降法应用于机器学习模型求解时，对特征的取值范围也是敏感的，当不同的特征值取值范围不一样时，相同的步长会导致尺度小的特征前进比较慢，从而走之字型路线，影响迭代的速度，甚至不收敛。

梯度下降法解方程

梯度下降法求解方程示例：为了迭代到取值为0的点，可采取对原函数取绝对值或者求平方作为损失函数。

在MindSpore中，通过mindspore.ops.GradOperation提供对任意函数式自动求导的支持。

在TensorFlow2中，通过GradientTape提供对自动微分的支持，它记录了求微分的过程，为后续自动计算导数奠定了基础。

 部分代码如下

### 求方程的根
class loss_func(ms.nn.Cell): # 用方程的平方作为求导目标函数
    def __init__(self):
        super(loss_func, self).__init__()
        self.mspow = ms.ops.Pow()       
    def construct(self, x):
        y = self.mspow(x, 3.0) + self.mspow(math.e, x)/2.0 + 5.0*x - 6
        y = self.mspow(y, 2) # 方程的输出的平方
        return y
x = ms.Tensor([0.0], dtype=ms.float32)
for i in range(200): # 200次迭代
    grad = GradNetWrtX(loss_func())(x)
    #print(grad)
    x = x - 2.0 * alpha * grad # 步长加大一倍
    print(str(i)+":"+str(x))

import tensorflow as tf
x = tf.constant(1.0)
with tf.GradientTape() as g:
    g.watch(x)
    y = x**3 + (math.e**x)/2.0 + 5.0*x - 6
dy_dx = g.gradient(y, x)
print(dy_dx)
>>> tf.Tensor(9.35914, shape=(), dtype=float32)
x = tf.constant(0.0)
for i in range(200):
    with tf.GradientTape() as g:
        g.watch(x)
        loss = tf.pow(f(x), 2)
    grad = g.gradient(loss, x)
    x = x – 2.0 * alpha * grad
    print(str(i)+":"+str(x))

 梯度下降法解线性回归问题

线性回归问题中m个样本的损失函数表示为：

回归系数的更新过程如下：

 

 

50000次迭代后效果如下

 

 部分代码如下

alpha = 0.00025
class loss_func2(ms.nn.Cell):
    def __init__(self):
        super(loss_func2, self).__init__()
        self.transpose = ms.ops.Transpose()
        self.matmul = ms.ops.MatMul()
        
    def construct(self, W, X, y):
        k = y - self.matmul(X, W)
        return self.matmul(self.transpose(k, (1,0)), k) / 2.0

class GradNetWrtW(ms.nn.Cell):
    def __init__(self, net):
        super(GradNetWrtW, self).__init__()
        self.net = net
        self.grad_op = ms.ops.GradOperation()
        
    def construct(self, W, X, y):
        gradient_func = self.grad_op(self.net)
        return gradient_func(W, X, y)
    
X = ms.Tensor((np.mat([[1,1,1,1,1,1], temperatures])).T, dtype=ms.float32)
y = ms.Tensor((np.mat(flowers)).T, dtype=ms.float32)
W = ms.Tensor([[0.0],[0.0]], dtype=ms.float32)
for i in range(50000):
    grad = GradNetWrtW(loss_func2())(W, X, y)
    #print(grad)
    W = W - alpha * grad
    print(i,'--->', '\tW:', W)

alpha = 0.00025
X = tf.constant( (np.mat([[1,1,1,1,1,1], temperatures])).T, shape=[6, 2], dtype=tf.float32)
y = tf.constant( (np.mat(flowers)), shape=[6, 1], dtype=tf.float32)

def linear_mode(X, W):
    return tf.matmul(X, W)

W = tf.ones([2,1], dtype=tf.float32)

for i in range(50000):
    with tf.GradientTape() as g:
        g.watch(W)
        loss = tf.reduce_sum( tf.pow(linear_mode(X, W) - y, 2) ) /2.0
    grad = g.gradient(loss, W)
    #print(grad)
    W = W - alpha * grad
    print(i,'--->', '\tW:', W)#, '\t\tloss:', loss)

随机梯度下降和批梯度下降

从梯度下降算法的处理过程，可知梯度下降法在每次计算梯度时，都涉及全部样本。在样本数量特别大时，算法的效率会很低。

随机梯度下降法（Stochastic Gradient Descent，SGD），试图改正这个问题，它不是通过计算全部样本来得到梯度，而是随机选择一个样本来计算梯度。随机梯度下降法不需要计算大量的数据，所以速度快，但得到的并不是真正的梯度，可能会造成不收敛的问题。

批梯度下降法（Batch Gradient Descent，BGD）是一个折衷方法，每次在计算梯度时，选择小批量样本进行计算，既考虑了效率问题，又考虑了收敛问题。

创作不易 觉得有帮助请点赞关注收藏~~~