因果推断 - 反事实
目录
- 基础知识
- 案例实战
版权:转载前请联系作者获得授权。
声明:部分内容出自因果关系之梯,已获得原作者授权。
参考书籍:《The Book of Why》——Judea Pearl
基础知识
定义:对于包含外生变量 U U U和内生变量 X X X和 Y Y Y的SCM,形如 Y X = x ( U = u ) = y Y_{X=x}(U=u)=y YX=x(U=u)=y表示“在 U = u U=u U=u的情况下,如果 X = x X=x X=x,则 Y = y Y=y Y=y”。其中, Y X = x ( U = u ) = y Y_{X=x}(U=u)=y YX=x(U=u)=y可以简写为 Y x ( u ) = y Y_x(u)=y Yx(u)=y。
反事实分析的一般步骤:
- 外展。基于数据对外生变量 U U U进行估算。
- 干预。利用 d o do do算子改变模型(删除指向 X X X的箭头),得到新模型 M x M_x Mx,反映我们提出的反事实假设。
- 预测。基于 U U U和 M x M_x Mx来计算结果。
以上三个步骤可以总结为:
因果推断第一定律: Y x ( u ) = Y M x ( u ) Y_x(u)=Y_{M_x}(u) Yx(u)=YMx(u)
反事实和干预的区别:
- 表现形式: d o ( x ) do(x) do(x) vs Y x Y_x Yx
- 对 X X X进行干预,不会对 X X X的子孙节点造成影响,而反事实会。
如何理解第2条?可以考虑如下因果图, P ( Y ∣ d o ( x ) ) P(Y|do(x)) P(Y∣do(x))和 P ( Y x ) P(Y_x) P(Yx)的含义显然不同。

- 计算 P ( Y ∣ d o ( x ) ) P(Y|do(x)) P(Y∣do(x))时, Y Y Y的结果实际上和 X X X的取值毫无关系,因为路径被 Z Z Z阻断了!
- 计算 P ( Y x ) P(Y_x) P(Yx)时,会根据 X = x X=x X=x对对应的 Z Z Z进行改动,进而得到 Y x Y_x Yx。
案例实战
下面基于一个案例,加深对反事实分析的理解。
在下表中,学历共分为 0 , 1 , 2 0,1,2 0,1,2三种,分别代表高中,本科,研究生。 S 0 ( u ) S_0(u) S0(u)表示雇员 u u u在学历是高中时,现有的工资水平, S 1 ( u ) S_1(u) S1(u)和 S 2 ( u ) S_2(u) S2(u)则是在本科和研究生学历下的工资水平。由于在工作时,每个人的学历已经固定,只会是高中、本科和研究生中的一种。故,对于每一个雇员,有两个工资的值为 ? ? ?,表示无法获得。
| 雇员 (u) | 工龄 EX(u) | 学历 ED(u) | 工资 S0(u) | 工资 S1(u) | 工资 S2(u) |
|---|---|---|---|---|---|
| Alice | 6 | 0 | 81000 | ? | ? |
| Bob | 9 | 1 | ? | 92500 | ? |
| Lucy | 9 | 2 | ? | ? | 97000 |
| Daivd | 8 | 1 | ? | 91000 | ? |
| Est | 12 | 1 | ? | 100000 | ? |
| Flxs | 13 | 0 | 97000 | ? | ? |
| … | … | … | … | … | … |
现在,我们想要研究一个反事实问题——如果Alice的学历是本科,那么她的工资应为多少?即:通过上表中的数据,估算 S 1 ( A l i c e ) S_1(Alice) S1(Alice)。
在不使用反事实分析的情况下,我们或许可以采用线性回归,通过统计得到你和数据的最佳直线:
S = 2500 × E X + 5000 × E D + 65000 S=2500 \times EX + 5000 \times ED + 65000 S=2500×EX+5000×ED+65000
并依此得出 S 1 ( A l i c e ) = 2500 × 6 + 5000 × 1 + 65000 = 85000 S_1(Alice)=2500 \times 6 + 5000 \times 1 + 65000 = 85000 S1(Alice)=2500×6+5000×1+65000=85000
但是,上述方法有一个明显的弊端,即:对于任何雇员,如果他们的工龄和学历一致,则预测出的工资也是一致的!通过观察Bob和Lucy的工资,我们可以发现,这显然是不对的!
从表中可以看出,Bob和Lucy具有相同的工龄,但Bob的学历更低。那么,假如Lucy的学历和Bob一致,二人的工资应该一致吗?答案显然是否定的。因为,如果Lucy降低了学历,那么理论上她的工龄会比Bob更长,这会导致 S 1 ( L u c y ) > S 1 ( B o b ) S_1(Lucy)>S_1(Bob) S1(Lucy)>S1(Bob)。
如何在模型中体现这一点呢?
我们还是通过线性回归拟合最佳直线,但是和上文中稍有不同:
S = 2500 × E X + 5000 × E D + 65000 + U S S=2500 \times EX + 5000 \times ED + 65000 + U_S S=2500×EX+5000×ED+65000+US
同时,我们还需要一个(可能是)下式的方程:
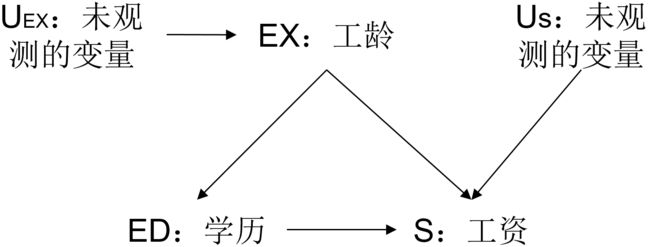
E X = 10 − 4 × E D + U E X EX=10-4 \times ED + U_{EX} EX=10−4×ED+UEX
有了这两个方程后,我们就可以根据反事实分析的三个步骤,计算 S 1 ( A l i c e ) S_1(Alice) S1(Alice):
- 根据数据估算出 U S = 1000 , U E X = − 1 U_S=1000, U_{EX} = -1 US=1000,UEX=−1;
- 使用 d o do do算子修改Alice的学历;
- 根据 U S = 1000 , U E X = − 1 U_S=1000, U_{EX} = -1 US=1000,UEX=−1计算出 E D = 2 ED=2 ED=2,再结合 E D = 1 ED=1 ED=1计算出 S 1 ( A l i c e ) = 76000 S_1(Alice)=76000 S1(Alice)=76000。