因果推断与反事实预测——利用DML进行价格弹性计算（二十四）

---

1 导言

1.1 价格需求弹性介绍

经济学课程里谈到价格需求弹性，描述需求数量随商品价格的变动而变化的弹性。价格一般不直接影响需求，而是被用户决策相关的中间变量所中介作用。假设 Q 为某个商品的需求的数量，P 为该商品的价格，则计算需求的价格弹性为，

通过上式可以简单知道，价格改变 1 元比价格改变 100 元，会导致更大的需求改变。比如以 5 元的价格每日可以卖 100 单位产品，如果价格需求弹性为 -3 ，那供应商将价格提升 5%（dp /P，从 5 元-> 5.25 元），需求将下降 15%（dQ/Q ，从 100->85）。那么收入将减少 1005-5.2585=53.75。
如果单价降低 5%，那么收入同理将提升 46.25。如果供应商知道了产品的价格弹性，那无须反复测试，即可清楚为提升收入到底应该是提价还是降价。

1.2 由盒马反事实预测论文开始

之前在因果推断笔记——DML ：Double Machine Learning案例学习（十六）这篇提到用DML求价格弹性，不过没有实操模块，本篇是在看过因果推断与反事实预测——盒马KDD2021的一篇论文（二十三） 盒马论文之后，想实操一下价格弹性这块。

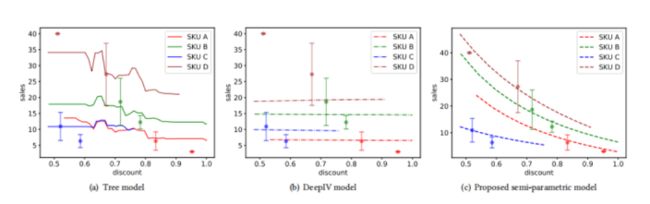
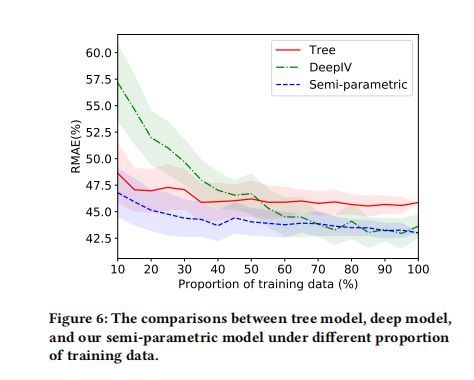
先来提一下盒马这篇，在反事实预测任务上（随着折扣改变销量如何改变）的尝试半参数模型、XGBtree模型、DeepIV：

• 第一种，半参数模型，不过这篇对动态折扣下销量的预估的半参数笔者还没深入了解，感觉用分层的价格弹性（平均折扣tree销量预测 + 价格弹性拟合动态折扣销量增量）来规避了核心因果推理的问题，后续要再理解一下该模型
• 第二种，错误尝试，将折扣当作treatment，动态将treatment作为特征来预测销量
• 第三种，deepIV，将三级品类的平均价格（treatment）作为工具变量

三者效果如图，还是semi-para好多了：

本篇是想放大价格弹性的因果计算模块，与盒马的不同：

• 推估弹性的方法不同（本篇是用DML预测）
• 粒度不同，本篇案例可没顾得上商品分类，一股脑子全放一起了，盒马那篇弹性系数是By 每个商品

1.3 DML - 价格弹性预测推理步骤

最好的方式，当然是直接进行 A/B 实验测试不同价格对用户的需求反应，但是价格这类的外生因素在同一产品同一阶段上，对不同用户展示不同的价格会直接损坏用户体验。因此从观察历史数据进行因果推断，但混杂因素（季节性、产品质量等）如何控制是因果推断的挑战。

这里采用 DML（Double Machine Learning） 方法进行因果推断，该方法主要解决两个问题：

• 第一，通过正则化挑拣重要控制变量；
• 第二，对比传统的线性回归模型，用非参数推断可以解决非线性问题。

DML 先应用机器学习算法去分别通过特征变量 X, W 拟合结果变量 Y 和处理变量 T，然后通过线性模型，使用处理变量的残差拟合出结果变量的残差。
目标是估计 ，这里的 Y 函数构成为 T 的因果作用和 X、W 的协同作用之和。

本篇整个价格弹性的推理过程：

1. 将数据分为两部分，一部分样本选用随机森林等模型，用混杂变量预测处理变量（价格 P），得到 E[P|X]；另外的样本同样可选择随机森林模型，用混杂变量预测结果变量（需求量 Q），得到 E[Q|X]。

2. 计算残差，得到不受混杂变量影响的价格 P 和 需求量 Q，即为 $P,Q$
   $P=P-E[P|X]$
   $Q=Q-E[Q|X]$

3. 因此直接将$P,Q$ 进行 log-log 回归就能得到弹性系数 :

文字推导一下：
若回归方程是:
$log(Y)=a+b\ast log(X)$，
则两边求导数得:
$(1/Y)\ast DY/DX=b\ast 1/X$，
所以:
$b=(DY/DX)\ast (X/Y)=(DY\ast X)/(DX\ast Y)=(DY/Y)/(DX/X)$
这个表达式正是弹性系数的定义公示。

需要得到$$\theta =\frac{dQ/Q}{dP/P}$$

倒推用log-log回归得到回归系数，即$$logQ～\theta \ast logP+截距$$

---

2 案例详解

与本节关联的文章：

• 因果推断与反事实预测——盒马KDD2021的一篇论文（二十三）
• 因果推断笔记——DML ：Double Machine Learning案例学习（十六）

下面的案例的来源：

• 利用机器学习因果推理进行弹性定价
• 数据分析36计(29)：价格需求弹性和因果推断
• 简单版代码：DML.ipynb
• 数据集来源：Association Rules and Market Basket Analysis

2.1 数据清理

数据集是kaggle的比赛数据集，原文ipynb直接读入的时候会格式报错，这里贴一段kaggle原生读入的方式，不会有报错：

data = pd.read_csv('OnlineRetail.csv',encoding= 'cp1252',parse_dates=['InvoiceDate'])
data = data.sort_values(by='InvoiceDate')
data = data.set_index('InvoiceDate')

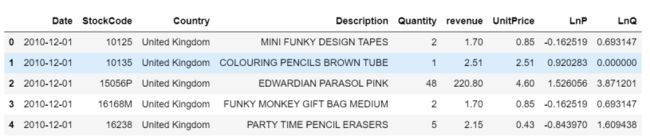
原数据是购物篮分析数据，这个数据集包含了一家英国在线零售公司在8个月期间的所有购买行为。

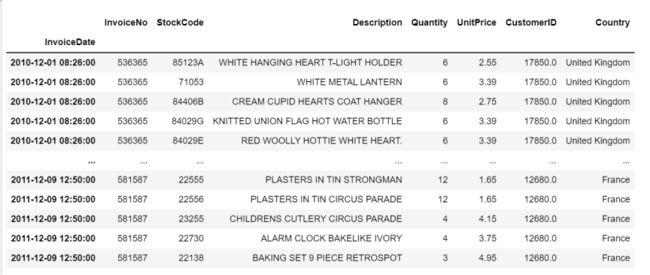
每个商品，在每个国家，每家店，每个时间出售的件数与对应的单价。
这里需要额外加工收入：

df['revenue'] = df.Quantity * df.UnitPrice

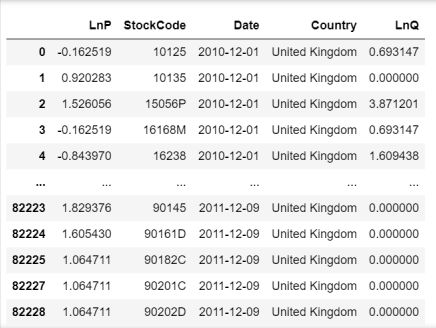
同时对P / Q进行对数化处理：

# 将单价和数量取log
df_mdl = df_mdl.assign(
    LnP = np.log(df_mdl['UnitPrice']),
    LnQ = np.log(df_mdl['Quantity']),
)

2.2 [v1版]求解价格弹性：OLS回归

v1版 = LnQ~LnP，没有协变量，用最简单的OLS回归

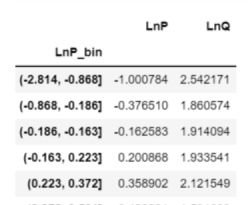
最简单的求解，也不管啥因果推断，有偏无偏，将上述数据的lnp和lnQ，一股脑子都分段，比如(-2.814,-0.868)就是这区间内lnp和lnQ的平均值，如下：

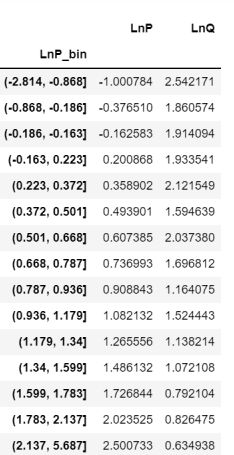
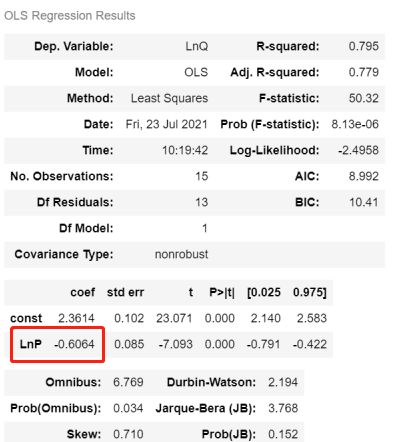
新生成的LnP和LnQ直接回归即得回归系数：

x='LnP'
y='LnQ'
df = df_mdl
n_bins=15
x_bin = x + '_bin'

df[x_bin] = pd.qcut(df[x], n_bins)

tmp = df.groupby(x_bin).agg({
    x: 'mean',
    y: 'mean'
})
# 回归
mdl = sm.OLS(tmp[y], sm.add_constant(tmp[x]))
res = mdl.fit()

得到结果：

弹性系数为-0.6064，价格越高，销量越少

v1的计算也可以使用另外一种方式，计算方差，
因为只有两个变量可以：

df_mdl[['LnP', 'LnQ']].cov()

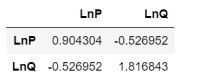
这里就是:
$\theta =\frac{-0.52}{0.9}=-0.60$

2.3 [v2版]求解价格弹性：Poisson回归+多元岭回归

v2版 = LnQ~LnP+Country+StockCode+Date，有多元协变量，用岭回归+泊松回归

import sklearn.preprocessing
from sklearn import linear_model
from sklearn.pipeline import Pipeline
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, StandardScaler, RobustScaler
from sklearn.feature_extraction.text import CountVectorizer

feature_generator_basic = ColumnTransformer(
    [
        ('StockCode', OneHotEncoder(), ['StockCode']),
        ('Date', OneHotEncoder(), ['Date']),
        ('Country', OneHotEncoder(), ['Country']),
        ('LnP', 'passthrough', ['LnP']),
    ], remainder='drop'
)

mdl_basic = Pipeline([
    ('feat_proc', feature_generator_basic),
    ('reg', linear_model.PoissonRegressor(
        alpha=1e-6,  # l2 penalty strength; manually selected value for minimum interference on LnP-coef (elasticity)
        fit_intercept=False, # no need, since we have OneHot encodings without drop
        max_iter=100_000, 
    )),
], verbose=True)

mdl_basic_ols = Pipeline([
    ('feat_proc', feature_generator_basic),
    ('reg', linear_model.Ridge(
        alpha=1e-20,  # l2 penalty strength, "very small"
        fit_intercept=False, 
        max_iter=100_000, 
    )),
], verbose=True)

mdl_basic.fit(
    df_mdl[['LnP', 'StockCode', 'Date', 'Country']], 
    df_mdl['Quantity'] # Poisson regression has log-link, so LnQ is implicit in loss function
)

但是训练数据不跟之前v1一样，不需要分组，直接用原始数据：

柏松回归中LnP的回归系数为 -2.87559，
Ridge—OLS回归中LnP的回归系数为 -1.79945，
尝试下来各个方法得到的结果差异很大。

2.4 [v3版]求解价格弹性：DML

2.4.1 DML数据准备 + 建模 + 求残差

因为不同产品的单价差异很大，所以对于同一维度的单价需要减去该维度的单价均值：
$dLn{P}_{i,t}=log(p_{i,t})-log({\overline{p}}_i)$

这里，消除数据差异的方法，在盒马论文里面是：

• $Y_i^{\text{o}}$是常规渠道产品$i$近期的平均销量
• $Y_i/Y_i^{\text{nor}}$代表了折扣价格使得销量增加的百分比，因为不同商品销量差异很大，所以比率会比绝对值更有用

df_mdl['dLnP'] = np.log(df_mdl.UnitPrice) - np.log(df_mdl.groupby('StockCode').UnitPrice.transform('mean'))
df_mdl['dLnQ'] = np.log(df_mdl.Quantity) - np.log(df_mdl.groupby('StockCode').Quantity.transform('mean'))

混杂因子也做了一些处理：

1. 季节性变量：该价格处于第几月、处于月里第几天和周里第几天
2. 产品上线的时长：用当期时间减去该产品的最小时间
3. sku 的价格水平：单个sku内的价格中位数

df_mdl = df_mdl.assign(
    month = lambda d: d.Date.dt.month,
    DoM =   lambda d: d.Date.dt.day,
    DoW =   lambda d: d.Date.dt.weekday,
    stock_age_days = lambda d: (d.Date - d.groupby('StockCode').Date.transform('min')).dt.days,
    sku_avg_p = lambda d: d.groupby('StockCode').UnitPrice.transform('median')
)

有了混杂因子，lnp,lnq，来看看DML过程：

• 构建$lnp-W$，$lnq-W$
• 计算残差

# 混杂因子针对Q \ P 分别建模
model_y = Pipeline([
    ('feat_proc', feature_generator_full),
    ('model_y', RandomForestRegressor(n_estimators=50, min_samples_leaf=3, n_jobs=-1, verbose=0)) 
    # n_samples_leaf/n_estimators is set to reduce model (file) size and runtime
    # larger models yield prettier plots.
])
model_t = Pipeline([
    ('feat_proc', feature_generator_full),
    ('model_t', RandomForestRegressor(n_estimators=50, min_samples_leaf=3, n_jobs=-1, verbose=0))
])

# 上述模型得到预估值
# Get first-step, predictions to residualize ("orthogonalize") with (in-sample for now)
q_hat = model_y.predict(df_mdl)
p_hat = model_t.predict(df_mdl)

# 用观测值减去预测得到的值求解残差
df_mdl = df_mdl.assign(
    dLnP_res = df_mdl['dLnP'] - p_hat,
    dLnQ_res = df_mdl['dLnQ'] - q_hat,
)

2.4.2 三块模型对比

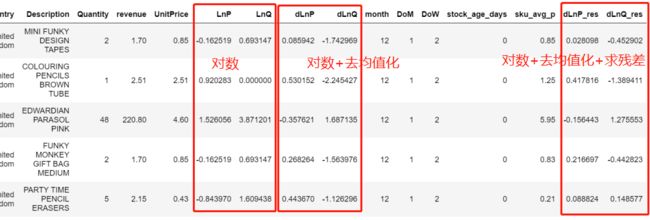
此时经过数据处理，数据集中就有三种数据类型：

• 对数
• 对数+去均值化
• 对数+去均值化+求残差
  
  然后三组数据，按照v1版的处理方式，先分段，后利用OLS求价格弹性：
  

# 初始ols模型
old_fit = binned_ols(
    df_mdl,
    x='LnP',
    y='LnQ',
    n_bins=15,
)
# 初始去均值化后的ols模型
old_fit = binned_ols(
    df_mdl,
    x='dLnP',
    y='dLnQ',
    n_bins=15,
    plot_ax=plt.gca(),
)
# 残差拟合的ols模型
old_fit = binned_ols(
    df_mdl,
    x='dLnP_res',
    y='dLnQ_res',
    n_bins=15,
    plot_title='Causal regression naively, with item controls, and after DML.',
    plot_ax=plt.gca()
)

此时经过数据处理，数据集中就有三种数据类型，三者的价格弹性对比：

• 对数：$\theta =-1.7$
• 对数+去均值化：$\theta =-1.7$
• 对数+去均值化+求残差：$\theta =-1.819$

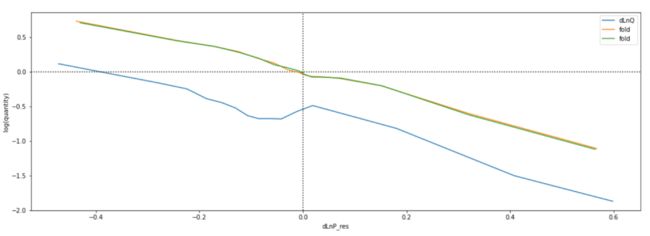
当然OLS还有截距项，绘图可得：

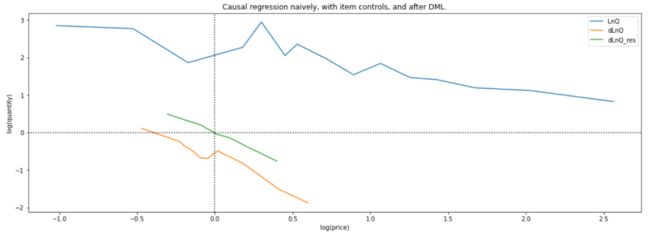
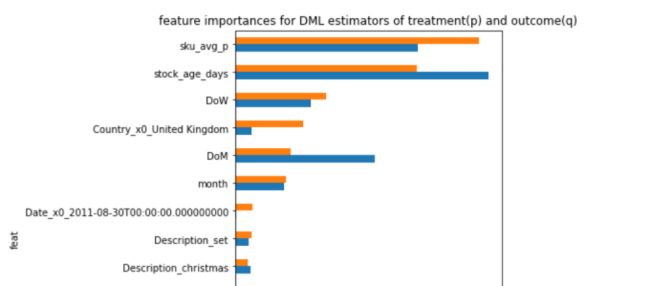
这里原文也给出了，DML求解过程中，两个随机森林模型的特征重要性：

feat_imp = pd.DataFrame({
    'feat': get_feat_generator_names(model_y['feat_proc']),
    'importance_q': model_y['model_y'].feature_importances_,
    'importance_p': model_t['model_t'].feature_importances_,
}).set_index('feat')

feat_imp.sort_values(by='importance_p').iloc[-15:].plot.barh(
    figsize=(5, 8), 
    title='feature importances for DML estimators of treatment(p) and outcome(q)'
)

2.4.3 稳健性评估

这章主要学习到的：

• 一种数据筛选的原则，残差正交化后，$dLn{P}_{res}$ 总是很小，因此为了减少噪音，我们将丢弃所有非常小的价格变化观察值，它们不包含太多信息
  训练数据分成多k-fold来检验弹性系数的稳定性

那么在盒马那篇文章里面来看一下这个图，
使用training data的比例往上几个模型的稳定性分布情况

模型的预测推断结果是
$\hat{\theta }=\frac{dLn{Q}_{res}}{dLn{P}_{res}}$

但是残差正交化后，$dLn{P}_{res}$ 总是很小，因此为了减少噪音，我们将丢弃所有非常小的价格变化观察值，它们不包含太多信息。

Chernozhukov 提出了一个改进的 DML，传统的标准 OLS 方法估计
$\hat{\theta }=(P^{T}P{)}^{-1}{P}^{T}Q$
但改进的
$\hat{\theta }=(P^{T}P{)}^{-1}{P}^T{Q}^T$
即第二个 P 矩阵用未残差化的。

最后采取 2-fold 得到平均值使得结果更稳健，最终弹性系数结果为 -1.89

old_fit = binned_ols(
    df_mdl,
    x='dLnP',
    y='dLnQ',
    n_bins=15,
    plot_ax=plt.gca(),
)
plt.gca().set(
    xlabel='log(price)',
    ylabel='log(quantity)',    
)
plt.gca().axvline(0, color='k', linestyle=':')
plt.gca().axhline(0, color='k', linestyle=':')


elast_estimates = list()
for idx_aux, idx_inf in KFold(n_splits=2, shuffle=True).split(df_mdl):
    
    df_aux = df_mdl.iloc[idx_aux]
    df_inf = df_mdl.iloc[idx_inf].copy()
    
    # step 1: aux models and residualize in inferential set
    print('fitting model_y')
    model_y.fit(df_aux, df_aux.dLnQ)
    print('fitting model_t')
    model_t.fit(df_aux, df_aux.dLnP)
    
    df_inf = df_inf.assign(
        dLnP_res = df_inf['dLnP'] - model_t.predict(df_inf),
        dLnQ_res = df_inf['dLnQ'] - model_y.predict(df_inf),
    )
    
    binned_ols(
        df_inf,
        x='dLnP_res',
        y='dLnQ_res',
        n_bins=15,
        plot_ax=plt.gca(),
        label='fold'
    )
    
    # ignore observations where we residualized away all variation in price
    mask = (~(df_inf.dLnP_res.abs() < 0.01))
    df_inf_censored = df_inf[mask]
    
    # step 2.1: Chernozhukov DML inference
    elast = (
        df_inf_censored['dLnP_res'].dot(df_inf_censored['dLnQ_res'])
        /
        df_inf_censored['dLnP_res'].dot(df_inf_censored['dLnP'])
        # the last part here deviates from standard OLS solution
    )
    
    print('DML elast: ', elast)
    elast_estimates.append(elast)

    print('OLS elasticity for comparison:',
        df_inf_censored['dLnP_res'].dot(df_inf_censored['dLnQ_res'])
        /
        df_inf_censored['dLnP_res'].dot(df_inf_censored['dLnP_res'])
    )    

print("DML efficient estimate of elasticity:", np.mean(elast_estimates))

这里远程再对比一下盒马的那篇，貌似媲美他们的半参数模型？

---

3 回顾-Econml官方折扣营销案例

这里回顾一下econml的一个官方案例，因果推断笔记——因果图建模之微软开源的EconML（五） 之前记录过，
github链接为：Case Study - Customer Segmentation at An Online Media Company.ipynb

比较相关的另一篇:
因果推断笔记——DML ：Double Machine Learning案例学习（十六）

当然本节不摘录，只是回顾一下该案例中的一些关于弹性系数的重要细节。

3.1 数据结构

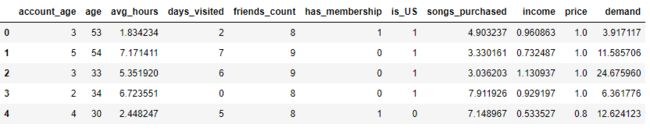
数据格式为：

Feature Name	Type	Details
account_age	W	user’s account age
age	W	user’s age
avg_hours	W	the average hours user was online per week in the past
days_visited	W	the average number of days user visited the website per week in the past
friend_count	W	number of friends user connected in the account
has_membership	W	whether the user had membership
is_US	W	whether the user accesses the website from the US
songs_purchased	W	the average songs user purchased per week in the past
income	X	user’s income
price	T	the price user was exposed during the discount season (baseline price * small discount)
demand	Y	songs user purchased during the discount season

数据集*有~ 10000个观察，包括9个连续和分类变量，代表用户的特征和在线行为历史，如年龄，日志收入，以前的购买，每周以前的在线时间等。

那么这里的：

• 其他变量：Z/W - account_age ~ songs_purchased - W - 混杂因子
• income - X - 考察变量 - 用户收入
• demand - Y - outcome - 销量
• Price - T - 干预，折扣，取值为[1,0.9,0.8]，根据下面的公式的来

3.2 训练后的系数含义-> 收入弹性

# Get log_T and log_Y
log_T = np.log(T)
log_Y = np.log(Y)

# Train EconML model
est = LinearDML(
    model_y=GradientBoostingRegressor(),
    model_t=GradientBoostingRegressor(),
    featurizer=PolynomialFeatures(degree=2, include_bias=False),
)
est.fit(log_Y, log_T, X=X, W=W, inference="statsmodels")
# Get treatment effect and its confidence interval    得到治疗效果及其置信区间
te_pred = est.effect(X_test)

# Get the final coefficient and intercept summary
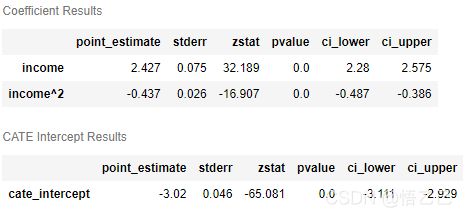
est.summary()

输出结果：

解读一下含义：

• 第一点，非常重要的是,Y和T都取了对数，这样是标准的弹性log-log公式，可以求得弹性系数
• 系数项是 income-X -> sale-Y 即为需求-收入的弹性系数；
  • 当收入小于1时，弹性在-1.75左右
  • 当收入大于1时，有一个较小的负值
  • 观察P值，影响是显著的
• 截距项=CATE，此时为-3.02，则代表，$Y(T=1)-Y(T=0)$为负数，代表整体来看，有折扣反而对销量不利

另外，
这里可以看到，如果要考虑计算CATE，那么此时，最终所求的回归系数：
就是 $销量Y-收入income$的弹性系数，
而并非$销量Y-Price折扣$的价格弹性系数。

对比案例2，其中Q销量（Y），P价格（T），最终模型求得的就是价格弹性，此时为啥不能求价格弹性，而是收入~销量的弹性？

此时就要来看看，DML求ATE和CATE之间的差异了:

求ATE：

• 两个平行模型：M1(Y~X) 和 M2(T~X)
• $\widetilde{Y_i}=\alpha +{\beta }_1\widetilde{T_i}+{ϵ}_i$

求CATE：

• 仍然两个平行模型M1(Y~X) 和 M2(T~X)
• $\widetilde{Y_i}=\alpha +{\beta }_1\widetilde{T_i}+{\beta \text{β}\beta }_2{X}_i\text{Xi}{X}_i\widetilde{T_i}+{ϵ}_i$

从CATE的公式可以看到，线性回归在ATE求解的时候，只有T，那么在CATE求解的时候，是X|T的交互项，所以不是单纯的价格弹性

3.3 Uplift的CATE预测功能

额外参考Uplift相关文章：
智能营销增益（Uplift Modeling）模型——模型介绍（一）

主要是看：est.effect(X)

est.effect(np.array([[1],[1]]))
>>> array([6.07165998, 6.07165998])

其中我们来看一下est.effect(np.array([[1],[2]]),T0=0, T1=1) 算的是啥，
之前笔者也有点混淆，该函数算出的是CATE(或者我这边用异质性个体平均处理效应)，在X=1下，Y(T=1)-Y(T=0) => CATE
而这个结果并不是跟之前机器学习里面的，model.predict(X)一样，而是一种增量的表现。所以，常用于价格弹性的计算。

那么笔者在本小节使用的是Uplift，要说明的是，Uplift模型中也是需要预测某些新样本的增量关系，
那么此时介绍的这个函数以及应用也是比较适配的

当然，比如此时,X=1下的CATE为：6.07
有着两种问题:

• 大于0，说明，X=1的情况下，有优惠券还是好的
• 那6.07这样的差异，属于明显差异还是不明显？该如何选择样本，这个econml后面有两个模块是来解释的这个的

3.4 SingleTreePolicyInterpreter 和SingleTreeCateInterpreter

贴一下两个模块的图：

3.4.1 X|T~Y分析：SingleTreeCateInterpreter哪些用户比较积极/消极

EconML包括可解释性工具，以更好地理解治疗效果。

官方可解释性Interpretability的文章中提到：
:class:.SingleTreeCateInterpreter trains a single shallow decision tree for the treatment effect $\theta (X)$ you learned from any of our available CATE estimators on a small set of feature X that you are interested to learn heterogeneity from.
The model will split on the cutoff points that maximize the treatment effect difference in each leaf.
Finally each leaf will be a subgroup of samples that respond to a treatment differently from other leaves.

治疗效果可能很复杂，但我们通常感兴趣的是一些简单的规则，这些规则可以区分哪些用户对提议的变化做出积极回应，哪些用户保持中立，哪些用户做出消极回应。

EconML SingleTreeCateInterpreter通过训练由任何EconML估计器输出的处理效果的单一决策树来提供可解释性。

intrp = SingleTreeCateInterpreter(include_model_uncertainty=True, max_depth=2, min_samples_leaf=10)
intrp.interpret(est, X_test)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=X.columns, fontsize=12)

在下图中，我们可以看到暗红色的用户(income < 0.48)对折扣反应强烈，白色的用户对折扣反应轻微。

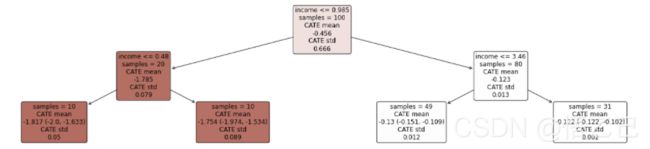
SingleTreeCateInterpreter 与 SingleTreePolicyInterpreter 的差异：

• 前者代表，根据处理效应，拆分人群，人群之间的差距较大；
• 后者代表，找出 能发券 / 不能发券的界限

3.4.2 T~X分析：SingleTreePolicyInterpreter 什么收入的人该打折

该模型的解释，参考Interpretability，找出 该发 or 不该发优惠券的群体：
Instead of fitting a tree to learn groups that have a different treatment effect（上个模块SingleTreeCateInterpreter的含义）, :class:.SingleTreePolicyInterpreter tries to split the samples into different treatment groups.
So in the case of binary treatments it tries to create sub-groups such that all samples within the group have either all positive effect or all negative effect.
Thus it tries to separate responders from non-responders, as opposed to trying to find groups that have different levels of response.
This way you can construct an interpretable personalized policy where you treat the groups with a postive effect and don’t treat the group with a negative effect. Our policy tree provides the recommended treatment at each leaf node.

我们希望做出政策决定，使收入最大化，而不是需求最大化。
在这个场景中,收入的计算公式为：

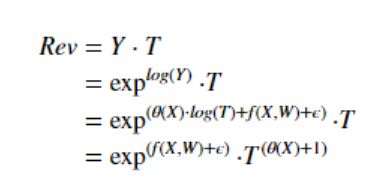
随着价格的降低，只有当$\theta (X)+1<0$时，收入才会增加。
因此，我们在这里设置sample_treatment_cast=-1，以了解我们应该给哪种类型的客户一个小的折扣，以使收入最大。

intrp = SingleTreePolicyInterpreter(risk_level=0.05, max_depth=2, min_samples_leaf=1, min_impurity_decrease=0.001)
intrp.interpret(est, X_test, sample_treatment_costs=-1)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=X.columns, treatment_names=["Discount", "No-Discount"], fontsize=12)

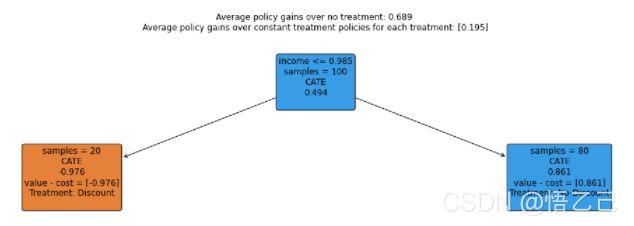
EconML库包括“SingleTreePolicyInterpreter”等策略可解释性工具，该工具可以计算治疗成本和治疗效果，以了解关于哪些客户可以获利的简单规则。
从下图中我们可以看到，模型建议对收入低于$0.985$的人给予折扣，对其他人给予原价。

SingleTreeCateInterpreter 与 SingleTreePolicyInterpreter 的差异：

• 前者代表，根据处理效应，拆分人群，人群之间的差距较大；
• 后者代表，找出 能发券 / 不能发券的界限

3.4.3 小结

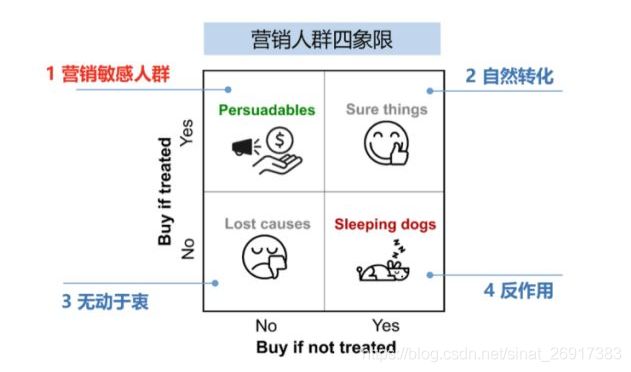
如果按照uplift使用场景，来看一下下图，营销敏感人群如何定义，是本节想要表达的：

这里YY一下使用场景，假设我已经Train了一个优惠券/折扣 模型，然后对一批新样本计算uplift，那么此时我可以用est.effect()，这时候就可以得到这些人的CATE，此时：

• SingleTreeCateInterpreter 可以告诉你，CATE的分界点，挑选x-income < 0.48（CATE = -1.785）的CATE绝对值比较大，这些人属于折扣敏感人群（这里敏感 = 喜欢 + 反感 ），当然这里只是一条规则，而且是限定在income上的规则
• SingleTreePolicyInterpreter告诉你，哪些适合发，哪些不适合发，准则就是收入最大

---

4 反事实预测的数据结构与粒度

反事实预测其实本质还是预测，回看一下以上的几个案例的数据结构

盒马论文里面
需要对每个商品，每个门店进行预测，这个粒度有点夸张了

案例3的数据结构值得简单分析一下：

数据集有~ 10000个观察，包括9个连续和分类变量，代表用户的特征和在线行为历史，如年龄，日志收入，以前的购买，每周以前的在线时间等。

那么这里的：

• 其他变量：Z/W - account_age ~ songs_purchased - W - 混杂因子
• income - X - 考察变量 - 用户收入
• demand - Y - outcome - 销量
• Price - T - 干预，折扣，取值为[1,0.9,0.8]，根据下面的公式的来

来看一下上述数据结构，是按人groupby-aggregate，所以这里CATE的含义是，
每个人，随着折扣的增加，需求量demand的变化情况

但如果YY一下盒马论文数据，如果，按照商品groupby-aggregate的话，这里的CATE的含义是，
每个商品，随着折扣的增加，需求量demand的变化情况

其实这里求得就是单个商品的销量预测了

再来看看案例2的数据结构中，
是按照price分组汇总了，这里P~Q，就是总量，预测的就是所有销量的信息

所以，仔细看一下案例2的数据集
可以做几类预测目标：

每个商品，在每个国家，每家店，每个时间出售的件数与对应的单价。
那么可以做：

• 可以预测，每个人购买商品数量Y的变动情况，T折扣（案例3）
• 可以预测，每个商品销售量Y/订单数/购买人数 的变动情况（盒马）
• 可以预测，所有商品的 销售量Y/订单数/购买人数（如案例2）

---

5 阿里飞猪 - 反事实预测模型

20220129更新，回看之前的案例：
【因果推断在阿里飞猪广告算法中的实践】

假如我们直接做预估模型，

• 特征选择：
  选取SRP（结果搜索页，一部分是广告，一部分是非广告）的特征，
  和广告本身的特征（包括pCTR、pCVR，以及单个treatment的embedding）；
• 模型目标：
  模型预测某一条用户请求是否产生订单（listing to order）的概率。

5.1 baseline - Treatment直接做特征

与【1.2 由盒马反事实预测论文开始】的第二种方法一样，直接把treatment作为特征，

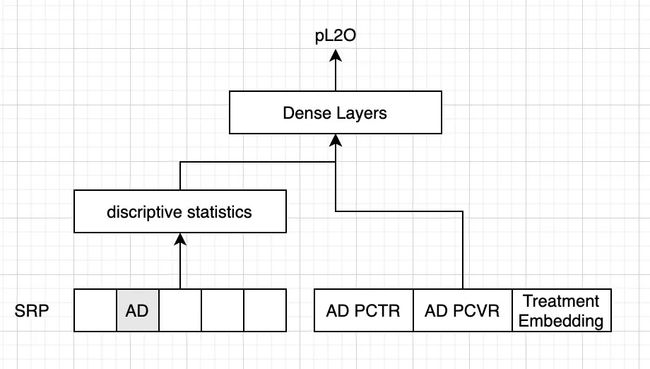
将“广告是否投放”这一treatment作为一般特征。模型的baseline是基于pCTR/pCVR（包括最好商品的CTR/CVR，以及广告商品的CTR/CVR和最好商品的CTR/CVR的差距）进行预估，预估任务的AUC还算理想（0.736），但是评价广告效应的Uplift Qini指数是负值；增加DNN后AUC有所提升，但是Uplift指数会变得更差。

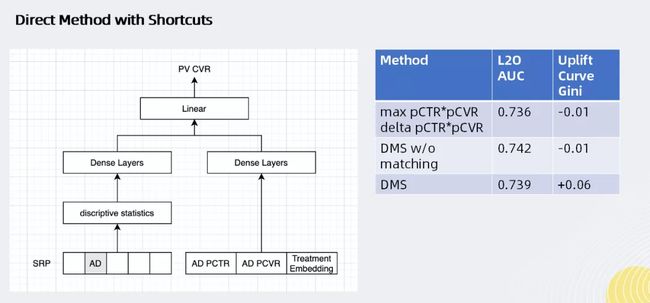
5.2 改进方案一：Direct Method with shortcuts

与Baseline相比，一些AD特征会再进入一个dense layers

将所有特征都连到一个DNN里面，采用了ResNets的思想，如上图所示：左侧网络对用户搜索请求预期的转换效率进行建模，右侧网络对“广告是否投放”产生的影响进行建模，最后通过线性模型加以合并。
对于广告效应的推断方面，这种模型相比于DNN会有一定的提升（uplift Qini指数提升至0.6）。

5.3 多任务学习：Dimain-Adaption: Multi-task Learning

与Baseline相比，两类特征进入一个共享层之后，会变成两个任务；然后再把两个任务相加，
这个与【1.2 由盒马反事实预测论文开始】中主要讲述的那种半参数模型类似，是一个加性模型，把控制组和对照组分开来

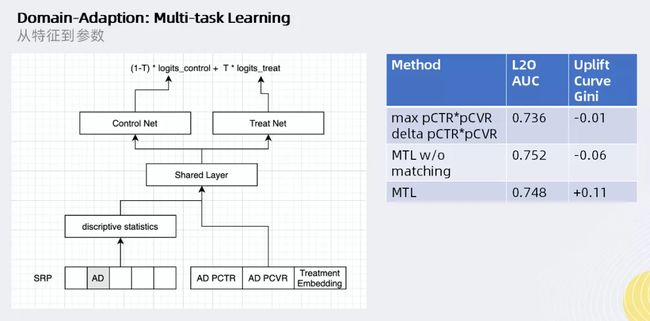
借助领域自适应中的多任务学习方法，将“是否投放广告”作为两个不同的任务（而不是一个任务中的二级特征）进行分别预估，通过建立完全不同的网络来学习“是否投放广告”产生的效果。
在重采样后的样本拟合后，uplift指数可提升至0.11。然而这种方法更容易对数据分布过拟合，从上图的右表也可以看出，对于未重采样的原始样本，uplift指数反而会更差。

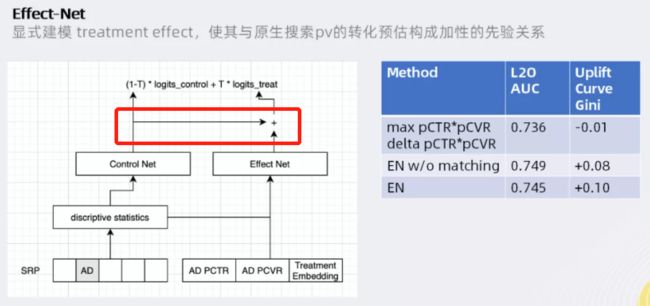
5.4 Effect-Net 显性建模

与多任务主要的改动，体现在control 特征还会加入到treatment模型之内

显式建模单变量treatment效应，即从模型的结构上体现目标效应的作用方式。
类似于前文所述的改进思路一，使用两个网络分别对预测效果和广告投放相应；
与思路一不同的是，在模型结构上可以显式地体现出业务理解的先验，即最后一层的模型融合部分，显示地将控制组的输出与uplift相加，得到最终的预测值。

使用Effect-Net方法，由于强先验知识的引入，在原始样本（即未重采样的有偏样本）的表现效果最好。