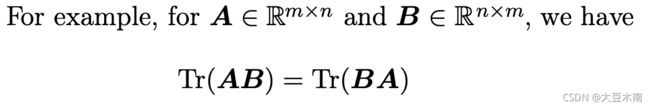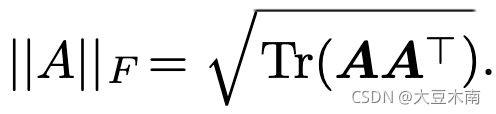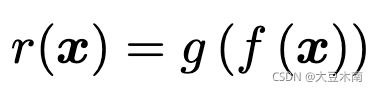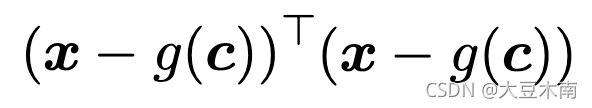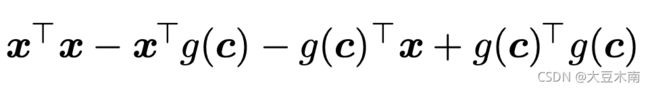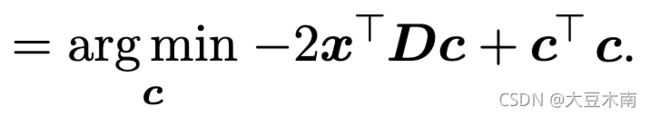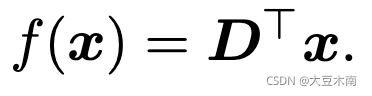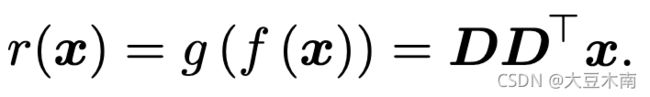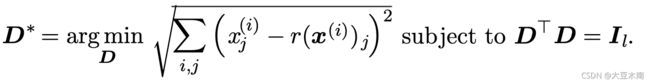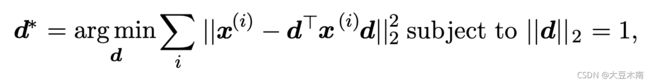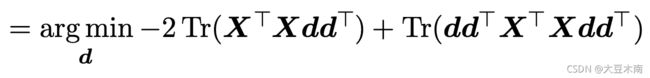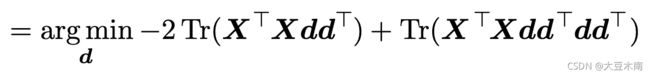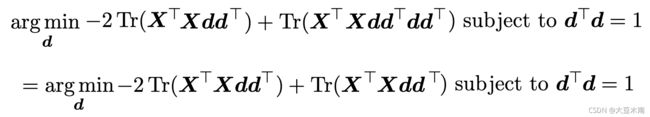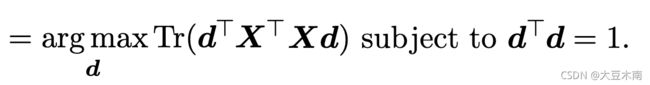主成分分析（PCA）（principal component analysis）
本文主要讲PCA的相关数学推导。PCA的数学推导用线性代数的知识就可以完成。
参考deeplearningbook.org一书2.12 Example: Principal Components Analysis
参考李航统计学习方法第16章主成分分析
本文的目录如下：
目录
用到的知识点
PCA 数学推导
PCA去中心化
基于奇异值分解的计算方法
结论
我们先讲两个用到的线性代数知识点：
用到的知识点
1、矩阵对角线元素之和（the trace operator）
矩阵对角线元素之和（the trace operator）,记做 Tr ，定义如下：
它有如下的性质：
1一个矩阵的trace等于它的转置的trace
2 循环置换性
2、矩阵的 Frobenius norm ：
它有如下的性质：
好啦，两个小知识点说完，就开始PCA啦～
PCA 数学推导
我们有 
空间上的 m 个点
，每一个点都是 n 维的向量。我们把这些点存起来， 要用 
个单位内存空间，如果我们空间有限，能不能用更少的空间存储和原来差不多的信息，使得信息减少尽可能的小。一个方法就是降维，对于每个点 
，我们找到这个点对应的的 
，并且 
，这样就可以减少原始数据的存储空间，用数学表达式表示出来就是
，
，这里的 
指 
，
指 
，为了看着方便，我们后边就用 和 
表示任意点的原始向量和降维之后的向量，
函数是编码函数（encoding function），
函数是解编码函数（decoding function）。
PCA就是提供了这样一种降维的方法。
开始正式推导啦～
PCA的推导先从解编码函数说起，为了使解编码函数尽可能简单，可以选择矩阵相乘的方式使得
，其中
。如果不做任何限制，计算最优的
比较困难，所以对 做一些限制的话看看能不能得到我们想要的效果。事实上我们可以假设 的每一列之间都是正交的，并且每一列是单位向量，对做了这个限制后计算最优的就比原来简单很多，并且我们可以得到这样的。
1、目标函数：
设
，其中，，我们的目标就是找到最优的 ：
2、用 表示 函数 ，因为，也就是用表示 ：
上述 第 1 步中的式子是一个求解最优值的式子。我们既然要求最优的，式子里就只能有已知的 和 未知的，现在式子里有个未知的 函数，我们需要先把函数也就是，用现有的和表示出来。
怎么表示呢？我们的目标是没有变的，我们可以先把第 1 步中的式子分解成每个样本的。然后求每一个最优的 ，求解最优的过程中， 我们认为和是已知的。求解最优的的式子如下：
可以转换成矩阵形式：
然后展开：
因为
和 
相等，都是一个实数，化简得：
省略掉
一项（因为与优化无关），得：
将 
换成 ：
因为任何矩阵乘单位阵不会发生改变，得：
我们运用矩阵微积分运算对 进行求导，令导数为0 ，我们得到：
我们已经求得最优的 啦，然后把它的表达式代入目标函数即可。
3、回到第 1 步中的目标函数
把 norm 转化成 norm 的平方；并假设 
，此时 就变成了一个向量，我们记做 
,则：
（我们这里先证明的情况，
时的推导和这差不多）
因为 
是个实数，所以我们可以把 移动到向量的左边：
因为 是个实数， 所以它的转置还是本身： 
我们可以把 
消掉，让
且
，用我们先前讲的Frobenius norm可得：
我们先不管限制项
，把前边的式子化简成矩阵形式，用到我们先前讲的第一个知识点：
然后我们将矩阵相乘展开：
我们用先前讲的
(把
当作
，
当作
) 可得：
同理，我们这次把
当作，当作可得：
不要忘了我们还有一个限制，，代入可得到：
先前讲的 ，(把
当作，
当作) 可得：
因为 
是个实数，可以把前边的
去掉：
subject to
到现在为止，已经化简到我们想要的形式了，是一个实对称矩阵， 所以能使 达到最大的 是对应最大特征值的特征向量，具体证明这里就不写了，可在网上搜搜～
我们证明证明的是 的特殊情况，当
时，![\boldsymbol{D}=[\boldsymbol{d}_{1},\boldsymbol{d}_{2} ]](http://img.e-com-net.com/image/info8/dfe432ce2ff043168d702f2d70642b3b.gif){kind=small}
，我们不难推出：
subject to 
, 
, 
，
使 
达到最大的 
是的最大特征值的特征向量。
在达到最大的基础上求最优的
， 是 与正交的单位向量，使
达到最大的 是的次大特征值的特征向量。
当
时，和等于2时是一样的道理。
PCA去中心化
在数学证明过程中，我们只需要求的前 
大特征值对应的特征向量就好了。但是有一个问题我们不得不考虑，那就是每一维数据的量纲差别大的问题。如果数据其中某一特征（矩阵的某一列）的数值特别大，那么它在整个误差计算的比重上就很大，那么投影在在新维度空间上的向量会去努力逼近最大的那一个特征，而忽略数值比较小的特征，在PCA前我们并不知道每个特征的重要性，这很可能导致了大量的信息缺失。所以去中心化是必要的。
去中心化后指的是：矩阵中每列各个数据要减去这列的平均值。
假设去中心化后的矩阵是
，那么PCA就是求 
的前 大特征值对应的特征向量。
事实上 
就是
的协方差矩阵。
基于奇异值分解的计算方法
传统的主成分分析通过数据的协方差矩阵的特征值分解进行，现在常用的方法是通过数据矩阵的奇异值分解进行。
通过数据的协方差矩阵的特征值分解求主成分就不多讲了，我们讲讲通过奇异值分解的方法求主成分。奇异值分解可参考奇异值分解（SVD）（Singular Value Decomposition）。
我们知道，对 的实矩阵 ，假设其秩为 
，
，则可将矩阵 进行截断奇异值分解：
定义一个新的 矩阵 
（是去中心化后的矩阵）
那么 
可以看到 
就是 的协方差矩阵 
。
主成分分许归结于求协方差矩阵的特征值和对应的单位特征向量，所以问题转化为求矩阵 的特征值和对应的单位特征向量。
假设的截断奇异值分解为
，那么 
的列向量就是 的前 k 主成分。于是，求的主成分可以通过求的奇异值分解来实现。
结论
PCA是一种降维方法。取的协方差矩阵 的前 大特征值对应的特征向量，将这些特征向量拼起来作为各个列 得到 解编码矩阵 。编码矩阵是
。
实现方法可对原数据矩阵的协方差矩阵求特征分解，也可对去中心化后的原数据矩阵求奇异值分解。
呼，终于完事啦～