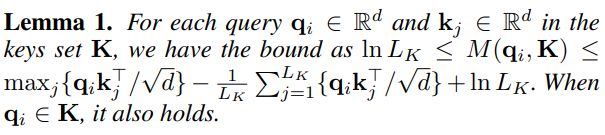Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting（2020-12-14）

模型介绍

对于长序列时间预测一直是研究的热点，随着预测序列长度增加，预测难度越来越高，LSTF需要模型提高预测能力，本文设计了一个高效的基于 Transformer 的 LSTF 模型，名为 Informer。informer模型成功地提高LSTF问题的预测能力，验证了类Transformer模型的潜在价值；Informer针对Transformer上的三大问题：二次时间复杂度，高内存消耗，Decoder逐步推理，制定提出解决方案：ProbSparse Self-Attention Mechanism ，自注意力蒸馏（self-attention distilling），生成式解码器（the generative style decoder）。

Self-Attention Mechanism的计算、内存和架构效率成为Transformer应用解决LSTF问题的瓶颈。Transformer模型主要存在下面三个问题：

• self-attention机制的二次计算复杂度问题：self-attention机制的点积操作使每层的时间复杂度和内存使用量为$O(L^2)$
• 高内存使用量问题：对长序列输入进行堆叠时，J个encoder-decoder层的堆栈使总内存使用量为$O(J\ast L^2)$，这限制了模型在接收长序列输入时的可伸缩性。
• 预测长输出时速度骤降：原始 Transformer 的动态解码操作导致 step by step inference（逐步推理）的速度如同基于 RNN 的模型一样慢。

Informer在Transformer基础上提出了三点改进：

• 提出了ProbSparse Self-attention机制，时间复杂度为 $O(LlogL)$，降低了常规 Self-Attention 计算复杂度和空间复杂度。
• 提出了self-attention蒸馏机制来缩短每一层的输入序列长度，序列长度短了，计算量和存储量自然就下来了。使用自注意蒸馏技术缩短每一层的输入序列长度，降低了 J 个堆叠层的内存使用量。
• 提出了生成式的decoder机制，在预测序列(也包括inference阶段)时一步得到结果，而不是step-by-step，直接将预测时间复杂度由$O(N)$降到了$O(1)$

模型结构

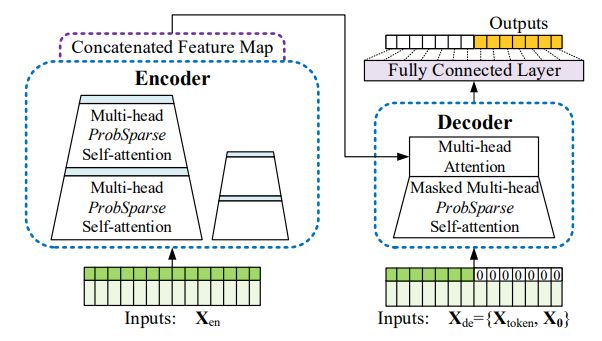
左侧是Encoder部分，它接收超长的输入数据（绿色部分）。然后将传统的Self-Attention层替换为本文提出的ProbSpare Self-Attention层。蓝色的部分是Self-Attention distilling操作来进行特征压缩。Encoder模块通过堆叠上述的两个操作来提高算法的鲁棒性。右侧是Decoder部分，它接收一系列的长序列输入，并将预测目标位置填充为0，再通过经过Mask的Attention层，最后一步生成预测输出（橙色部分）。

模型改进

ProbSparse Self-attention

标准的自注意力是由query、key、value的元组形式作为输入的一种缩放点积运算：

$Attention(Q,K,V)=Softmax(\frac{Q{K}^T}{\sqrt{d}})V$

其中 $Q\in R^{L_Q\times d},K\in R^{L_K\times d},V\in R^{L_V\times d},d$ 表示输入的维度。为了更好的讨论注意力机制，令$q_i,k_i,v_i$表示 $Q,K,V$的第 $i$ 行，则第 $i$ 个query的attention被定义成概率形式：

$A(q_i,K,V)={\sum }_{\begin{array}{l}j\end{array}}\frac{k(q_i,k_j)}{{\sum }_{l}k(q_i,k_l)}{v}_j=E_{p(k_j|q_i)}[v_j]$

其中，$p(k_j|q_i)=\frac{k(q_i,k_j)}{{\sum }_{l}k(q_i,k_l)}$, $k(q_i,k_j)$选择非对称指数核，self-attention通过结合概率 $p(k_j|q_i)$ 和 $v_i$ 获得输出。需要二次点积运算，所以时间复杂度和内存都是 $O(L_Q{L}_K)$，这是限制预测能力的主要原因。

之前的一些研究表明，self-attention具有潜在的稀疏性，即少数的点积贡献了大部分的attention，其他的点积贡献了次要的attention。主要的点积对促使相应的query的attention概率分布远离均匀（uniform）分布，也就是说序列中的某个元素只会和少数元素有较高的关联性。如果 $p(k_j|q_i)$ 接近于均匀分布 $q(k_j|q_i)=1/L_K$，self-attention就变成了value V的总和，对于输出来说是多余的。自然，分布概率p和q之间的“相似性”可以用来区分重要的query。这里使用KL散度来衡量p和q之间的相似性：

$KL(q||p)=ln{\sum }_{l=1}^{L_K}exp(q_i{k}_l^T/\sqrt{d})-\frac{1}{L_K}{\sum }_{j=1}^{L_K}{q}_i{k}_j^T/\sqrt{d}-ln{L}_K$

除去常量，将第i个query的稀疏性度量定义为：

$M(q_i,K)=ln{\sum }_{l=1}^{L_K}exp(q_i{k}_l^T/\sqrt{d})-\frac{1}{L_K}{\sum }_{j=1}^{L_K}{q}_i{k}_j^T/\sqrt{d}$

第一项是 $q_i$ 在所有key上的Log-Sum-Exp（LSE），第二项是它们的算术平均值。如果第i个query获得了较大的$M(q_i,K)$，则其attention概率p更具有区别性，且更有可能包含长尾self-attention分布的头部区域中的主要点积对。

基于所提出的度量，就可以通过每个key只关注u个主要的query来实现ProbSparse Self-attention：

$A(Q,K,V)=Softmax(\frac{\overline{Q}{K}^T}{\sqrt{d}})V$

$\overline{Q}$ 是一个和 q 有相同的大小的稀疏矩阵，它只包含了稀疏度量 $M(q,K)$ 下的前 u 个query。由一个恒定采样因子 c 控制，$u=c\cdot ln{L}_Q$，使得ProbSparse Self-attention为每一对query key的查找只需要计算$O(ln{L}_Q)$数量的点积，并且层的内存使用为$O(L_{K}ln{L}_Q)$。

然而，遍历度量$M(q_i,K)$所有的query需要计算所有的点积对，即$O(L_Q{L}_K)$。此外，由于LSE有潜在的数值稳定性。基于此，提出了一种取query稀疏性变量的经验近似方法。

根据引理1，建议的最大平均测量值为：

$\overline{M}(q_i,K)=\underset{j}{\max }\{\frac{q_i{k}_j^T}{\sqrt{d}}\}-\frac{1}{L_K}\sum _{j=1}^{L_K}\frac{q_i{k}_j^T}{\sqrt{d}}$

该式仅需要进行max，求和（点积）操作，比LSE简单。但是如果对每个query都进行稀疏性得分会带来额外的计算量，因此可以利用点积结果服从长尾分布的假设，从而在计算每个query稀疏性得分时，仅需要于采样的部分key进行计算就可以了。

在长尾分布下，只需要随机抽取$U=L_{K}ln{L}_Q$个点积对来计算$M(q_i,K)$，用零填充其他对。然后选取稀疏的top u作为$\overline{Q}$。实际上，query和key的输入长度通常都是相等的，即$L_Q=L_K=L$，这样，计算稀疏注意力的总时间、空间复杂度都是$O(LlnL)$。

Self-attention Distilling

作为ProbSparse注意力机制的自然结果，encoder的特征字典中会有 $V$ 的冗余组合，给占支配地位的特征赋予更高的权重，在下一层生成一个聚焦的注意力特征图（feature map）。受扩张卷积的影响，从第j层到第j+1层的蒸馏操作为：

$X_{j+1}^t=MaxPool(ELU(Conv1d([X_j^t{]}_{AB})))$

$[\cdot {]}_{AB}$表示注意力块，包含了Multi-head ProbSparse self-attention和一些重要的操作。$Conv1d(\cdot )$表示一个在时间维度上的卷积（卷积核长度为3），并使用ELU作为激活函数。在堆叠一层后，添加一个stride为2的最大池化层，并将$X^t$进行下采样来降低整个内存使用量到$O((2-ϵ)LlogL)$，$ϵ$是一个很小的数字。为了增强蒸馏操作的鲁棒性，使用减半输入构建主堆栈的副本，然后一次丢弃一层逐渐减少自注意力蒸馏层的数量，和金字塔一样，以便和输出的维度对齐。因此，将所有的堆栈输出连接起来，就形成了encoder最后的隐藏层输出。

Generative Style Decoder

使用标准的decoder结构，从结构图中看出由两个相同的Multi-head Self-Attention层堆叠而成。然而，使用生成式推断（直接输出多个token，不是一个一个输出token）来缓解长时间预测的速度骤降。在decoder中使用如下向量：

$X_{de}^t=Concat(X_{token}^t,X_0^t)\in R^{(L_{token}+L_y)\times d_{model}}$

$X_{token}^t\in R^{L_{token}+\times d_{model}}$为开始的token，$R^{L_{token}\times d_{model}}$是目标序列的占位符（将标量设置为0）。将mask的点积设置为$-\infty$将probSparse self-attention应用于masked multi-head attention。它可以防止每个位置关注未来的位置，从而避免自回归。一个全连接层来获得最终的输出，特大的$d_y$取决于是执行单变量预测还是多变量预测。

模型参考

论文地址：https://arxiv.org/abs/2012.07436

代码地址1：https://github.com/zhouhaoyi/Informer2020
代码地址2：https://github.com/zhouhaoyi/ETDataset