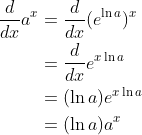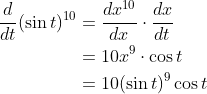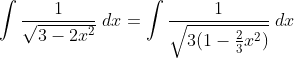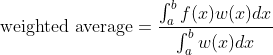老青蛙嘎嘎嘎

微积分基础-极限，导数，反导数

几何角度解释
物理角度解释

生理上知道如何画出切线，步骤为--先形象化几何问题，然后大脑就会找出答案，现在我们要从数学机理上分析人是以什么步骤画出切线的。

1. 瞬时变化率

平均变化率-平均速度

瞬时变化率-瞬时速度

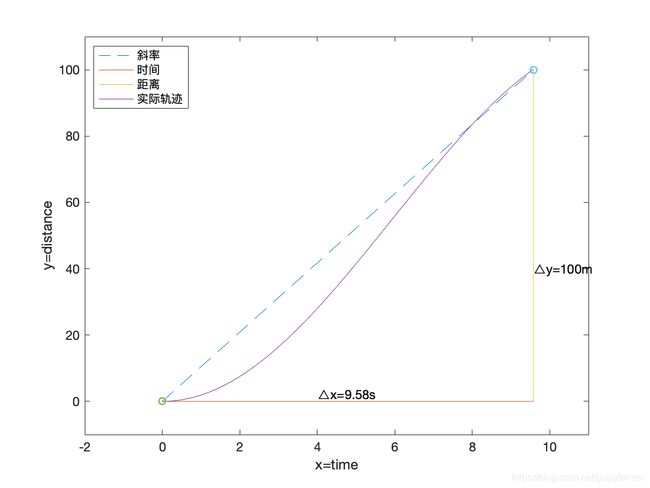
从平均速度引入瞬时速度比较合适。举例，对于平均速度来说，当时间差接近0时，平均速度就变成了瞬时速度

平均速度又等于两点的斜率，当时间差接近0时，斜率(瞬时斜率)又等于曲线切线的斜率，因此曲线切线的斜率就是瞬时速度

利用无限小增量的方式，就能得到某点的瞬时斜率

$avg \; speed = \frac{\Delta distance}{\Delta time} = \frac{\Delta y}{\Delta x} = \frac{dy}{dx} = \frac{100m}{9.58s} = 10.44 \; \frac{m}{s} = m \; or \; slope$

$instantaneous \; speed = \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}$

斜率就是两点之间的平均变化率

不指明方向叫速率，指明方向叫速度

2. 极限和连续

2.1 极限

极限是微积分的基础，尽管它非常重要，却是一个很简单的概念。极限又分为左极限和右极限。通常情况下，x 是变量，但对于极限情况，x 固定不变，Δx 是变量

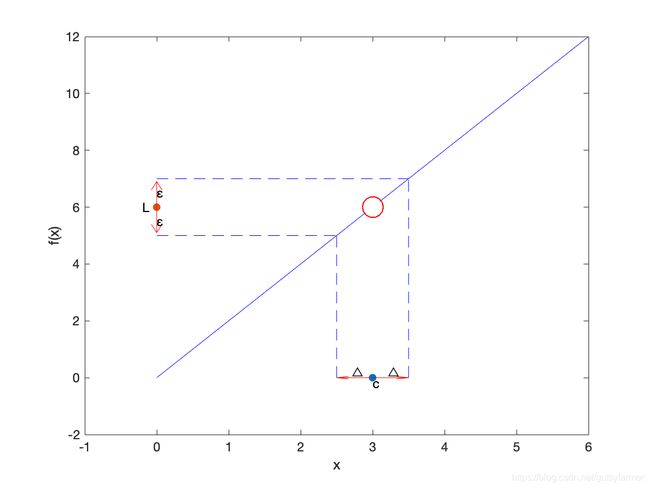
定义(epsilon delta definition)：对于给出的任何大于0的ε，无论ε等于多少，都存在一个大于0的Δ，使得当0<|x-c|<Δ时，0<|f(x)-L|<ε，那么就称L是函数f在x趋于c时的极限。本质上来说，可以无限接近极限值，是因为可以选取任何的ε。ε决定f(x)距极限值的距离

例子

1. 简单极限

$\lim_{x \rightarrow 4} \frac{x+3}{x^2+1} = \frac{7}{17}$

2. 导数极限

$\lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{x - x_0}$

例如：

$\lim_{x \rightarrow 0} \frac{\sin x}{x} = 1$

$\lim_{x \rightarrow 0} \frac{1 - \cos x} {x} = 0$

现在只有一种方法可以证明，即几何上的证明（一种指的是仅有几何，没有物理，而几何上的证明方法有多种，比如夹逼定理或此处的“极短曲线可以看作直线”等）

2.2 连续

f 在 x0 点连续，定义为 x -> x0 时 f(x) 的极限等于 f(x0)，即

$\lim_{x \rightarrow x_0} f(x) = f(x_0)$

连续函数的极限属于简单极限

2.3 可导必连续

3. 导数

几何角度的解释：曲线切线的斜率，又称导数（割线斜率求极限）

物理角度的解释：变化率（平均变化率求极限）

1. 几何角度的解释

直线斜率推广到曲线中，就有了导数

直线的斜率一直不变，曲线的斜率是变化的（曲线上某点的斜率等于该点切线的斜率）

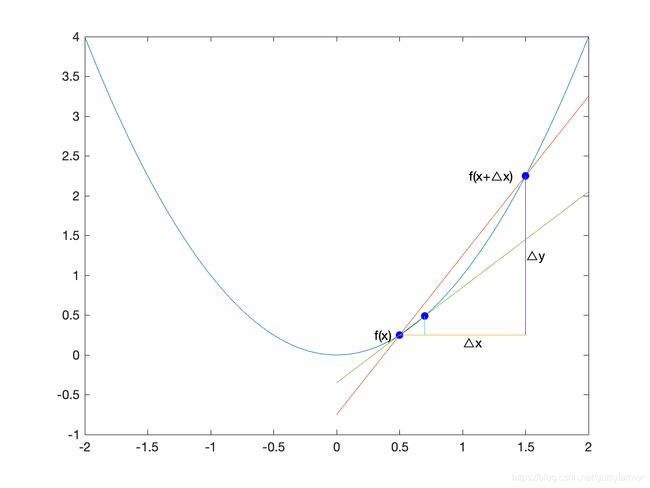
直线斜率->曲线割线的斜率->曲线切线的斜率

Δx很大时，割线斜率与确切点切线的斜率相差较大，但Δx很小时，割线斜率就与确切点切线的斜率很接近了；取割线斜率在Δx趋于0时的极限，割线斜率就等于确切点切线的斜率了，此时该极限式子又称为导函数，导函数的值称为导数，即某点切线的斜率：

$slope \; of \; line: \frac{f(b)-f(a)}{b-a}$

$slope \; of \; secant: \frac{f(x+\Delta x)-f(x)}{(x+\Delta x)-x} = \frac{f(x+\Delta x)-f(x)}{\Delta x}$

$derivative \; of \; f: f'(x) = \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}$

导函数的几种写法：

$f' = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx}y = \frac{d}{dx}f$

2. 物理角度的解释

平均变化率 -> 瞬时变化率：

$\frac{\Delta y}{\Delta x} \quad \rightarrow \quad \frac{dy}{dx}$

例子1（将x考虑为时间）：

$s = distance, \quad \frac{ds}{dt} = speed$

$q = charge, \quad \frac{dq}{dt} = current$

例子2（将x考虑为海拔高度）

$T = temperature, \quad \frac{dT}{dx} = temperature \;\; gradient$

求导公式分两种：对特定函数的求导、通用的求导法则

3.1. 特定函数的求导

求多项式、指数对数、三角函数等的导数

1. 幂函数的导数（n 为有理数）

$\frac{d}{dx} x^n = n x ^{n-1}$

2. 三角函数

$\frac{d}{dx} \sin x = \cos x$

$\frac{d}{dx} \cos x = - \sin x$

$\frac{d}{dx} \tan x = \frac{1}{\cos ^2 x}$

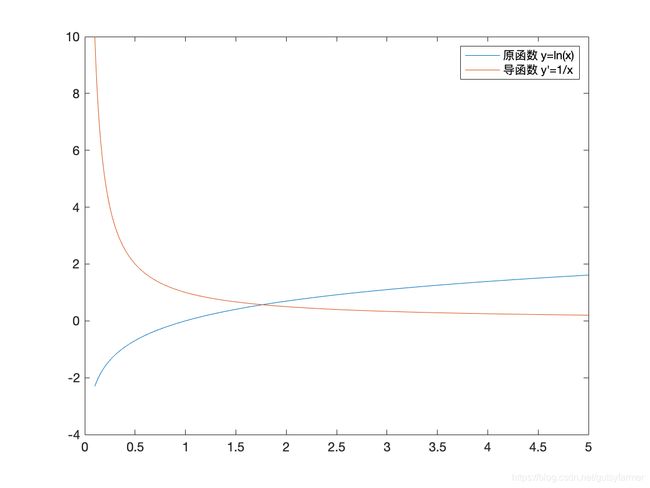
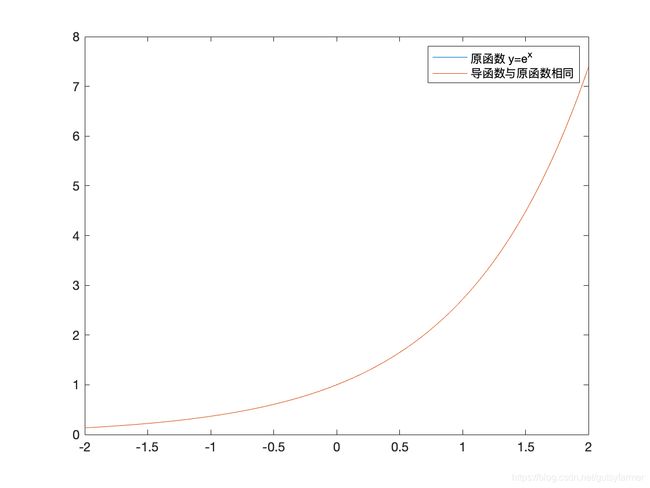
3. 指数和对数函数

$\frac{d}{dx} e^x = e^x$

$\frac{d}{dx} \ln x = \frac{1}{x}$

$\frac{d}{dx} a^x = (\ln a) a^x$

证明（没有按照上面的顺序）

$\begin{align*} \frac{d}{dx} x^n &= \lim_{\Delta x \rightarrow 0} \frac{(x+\Delta x)^n - x^n}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{ \sum_{k=0}^{n} (^n _k) x^{k-n} \Delta x ^k - x^n}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{x^n + (^n _1)x^{n-1} \Delta x + (^n _2) x^{n-2} \Delta x^2 + \cdots + \Delta x^n - x^n}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} (^n _1) x^{n-1} + (^n _2) x^{n-2} \Delta x + \cdots + \Delta x^{n-1} \\ &= (^n _1) x^{n-1} \\ &= n x^{n-1} \end{align*}$

证明1，已知 e 的定义（复利引入了e的定义）的情况下：

$\begin{align*} \frac{d}{dx} \ln x &= \lim_{\Delta x \rightarrow 0} \frac{\ln (x + \Delta x) - \ln x}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{1}{\Delta x} \ln \frac{x + \Delta x}{x} \\ &= \lim_{\Delta x \rightarrow 0} \ln (1+\frac{\Delta x}{x})^{\frac{1}{\Delta x}} \\ &= \lim_{n \rightarrow \infty} \ln (1+\frac{1}{n})^{\frac{n}{x}} \left \{ \frac{\Delta x}{x} = \frac{1}{n}, \Delta x = \frac{x}{n} \right \} \\ &= \lim_{n \rightarrow \infty} \ln ((1+\frac{1}{n})^n)^{\frac{1}{x}} = \frac{1}{x} \ln (\lim_{n \rightarrow \infty} (1+\frac{1}{n})^n) \\ &= \frac{1}{x} \end{align*}$

使用链式法则求导：

$\frac{d}{dx} \ln e^x = (\frac{d}{dx} e^x) \cdot (\frac{1}{e^x})$

又因为：

$\frac{d}{dx} \ln e^x = \frac{d}{dx} x \ln e = \frac{d}{dx} x = 1$

所以：

$\frac{d}{dx} \ln e^x = (\frac{d}{dx} e^x) \cdot (\frac{1}{e^x}) = 1$

$\frac{d}{dx} e^x = e^x$

此处为换底法，也可以使用对数微分法

$\begin{align*} \frac{d}{dx} \sin x &= \lim_{\Delta x \rightarrow 0} \frac{\sin (x+\Delta x) - \sin x}{ \Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{\sin x \cos \Delta x + \sin \Delta x \cos x - \sin x }{ \Delta x} \\ &= \lim_{\Delta x \rightarrow 0} ( \sin x (\frac {\cos \Delta x - 1}{\Delta x}) + \cos x \frac{\sin \Delta x}{\Delta x}) \\ &= \cos x \end{align*}$

上面的证明过程利用了“极限与连续”中的结论

3.2. 通用的求导法则

求导四则运算（加法法则，乘除法则），常乘数法则，链式法则，隐式函数微分法，对数微分法

$\frac{d}{dx}(f(x)+g(x))=\frac{d}{dx}f(x) + \frac{d}{dx}g(x) \qquad or \qquad (u+v)' = u' + v'$

$\frac{d}{dx} ( h(x) \cdot g(x)) =h'(x) \cdot g(x) + h(x) \cdot g'(x)$

$(u/v)' = \frac{u'v - uv'}{v^2}$

$\frac{d}{dx} h(g(x)) = g'(x) \cdot h'(g(x))$

证明

1. 乘法法则（多变量微积分的链式法则也可以证明该法则）

$\begin{align*} & \lim_{\Delta x \rightarrow 0} \frac{u(x+\Delta x)v(x+\Delta x) - u(x)v(x)}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{(u(x+\Delta x) - u(x)) v(x+\Delta x) + u(x)(v(x+\Delta x) - v(x))}{\Delta x} \\ &= \lim_{\Delta x \rightarrow 0} \frac{u(x+\Delta x) - u(x)}{\Delta x} v(x+\Delta x) + \lim_{\Delta x \rightarrow 0} u(x) \frac{v(x+\Delta x) - v(x)}{\Delta x} \\ &= u'v + uv' \end{align*}$

2. 除法法则证明过程类似于乘法法则

3. 链式法则

链式法则是一个合成规则，核心思想是换元法，掌握了链式法则，你能征服世界

$\frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} \qquad \Rightarrow \qquad u(v(x))' = u'(v(x)) \cdot v'(x)$

举例

$\frac{d}{dt} (\sin t) ^{10}$

$let \quad x = \sin t$

$\begin{align*} \frac{d}{dt} (\sin t)^{10} &= \frac{d x^{10}}{dx} \cdot \frac{dx} {dt} \\ &= 10 x^9 \cdot \cos t \\ &= 10 (\sin t)^9 \cos t \end{align*}$

3.2.1 隐函数微分法

隐式函数微分法：对于一个等式，不需要解出未知的函数，直接对等式两边微分的方法，称为隐式函数微分法

链式法则是非常给力的技巧，而隐函数微分则是一种更巧妙的代数方法，不用将等式表示成函数，因此叫“隐函数”。事实上，显式函数方法和隐式函数方法都可以用。隐式函数微分法主要用于求导任意反函数，只要知道原函数的导数就行。

例子1

$y = x^{\frac{m}{n}}$

$\frac{d}{dx}y^n = \frac{d}{dx}x^m$

因为 y 是 x 的函数，运用链式法则：

$\frac{d}{dy} \cdot \frac{dy}{dx} y^n = \frac{d}{dx}x^m$

$\frac{d}{dy}y^n \cdot \frac{dy}{dx} = \frac{d}{dx} x^m$

$n y^{n-1} \frac{dy}{dx} = m x^{m-1}$

$\frac{dy}{dx} = \frac{mx^{m-1}}{ny^{n-1}}$

将 y 带回去：

$\frac{dy}{dx} = \frac{mx^{m-1}}{n (x^{\frac{m}{n}})^{n-1}} = \frac{m}{n} x^{\frac{m}{n}-1}$

3.2.2. 对数微分法

对数微分法是处理指数函数的一个典型方法

例子（？有点循环证明的味道）

$a_k = (1 + \frac{1}{k})^k$

$\lim_{k \rightarrow \infty} (1+ \frac{1}{k})^k = e$

证明：

$set \quad \frac{1}{k} = \Delta x, \quad so \quad \Delta x \rightarrow 0 \quad when \quad k \rightarrow \infty$

$\begin{align*} a_k &= e^{\ln a_k} \\ &= e^{\ln (1+\frac{1}{k})^k} \\ &= e^{\ln (1+\Delta x)^{\frac{1}{\Delta x}}} \\ &= e^{\frac{1}{\Delta x} \ln (1 + \Delta x)} \\ &= e^{ \frac{ \ln(1+\Delta x) - \ln 1 }{\Delta x} } \end{align*}$

$\begin{align*} \lim_{k \rightarrow \infty} a_k &= \lim_{\Delta x \rightarrow 0} e ^ { \frac{\ln (1+\Delta x) - \ln 1}{\Delta x} } \\ &= e^{ (\frac{d}{dx} \ln x) |_{x=1} } \\ &= e^{\frac{1}{x} | _{x=1}} \\ &= e \end{align*}$

3.3. 导数的应用

线性近似，二阶近似，曲线画图，牛顿迭代法，中值定理

4. 微分、积分

定义：如果有一个函数 y = f(x)，那么 y 的微分记做 dy ，且定义为 dy = f'(x) dx 。两边同时除以 dx ，就是导数的定义。该记法的思想是用 dx 代替 Δx，dy 代替 Δy

反导函数定义（由微分的定义引出）：

$G(x) = \int g(x) dx$

大 G(x) 为小 g(x) 的反导函数，又称不定积分。为什么称为不定积分？是因为 C 无法确定，因此无法给出一个确定的函数

积分唯一性：

$\text{ if } F' = G' \quad \text{then} \quad F(x) = G(x) +C$

事实上，积分比求导难很多，有时甚至积不出来，所以积分有很多技巧，例如变量代换

特定函数的反导

多项式、三角函数，指数对数的反导，以及其它函数的反导（三角代换）

$\int x^n \; dx = \frac{1}{n+1} x^{n+1} + C$

$\int \sin x dx = - \cos x + C$

$\int \frac{1}{x} dx = \ln \left | x \right | + C$

$\int e^x dx = e^x$

$\int \frac{1}{\sqrt{1 - x^2}} dx = \sin^{-1} x + C$

$\int \frac{1}{1 + x^2} dx = \tan^{-1} x + C$

通用的反导法则(积分法则)

加法、常乘数、反乘法法则，反乘法法则又推导出了分部积分，反链式法则，定积分性质，部分分式展开（拉普拉斯变换中也有此方法，即把函数转换为容易积分的分式）

$\int (f(x) + g(x)) dx = \left $\int f(x) dx + \int g(x) dx \right $ + C$

$\int C f(x) dx = C \int f(x) dx \quad (\text{C doesn't depend on x})$

$\int \left $ f'(x) \;g(x) + f(x) \;g'(x)\right $ dx = f(x) \; g(x)$

分部积分（比反乘法法则更有用，每进行一次，f(x)的指数会降低一次）：

$\int f(x) \; g'(x) dx = f(x)g(x) - \int f'(x) g(x) dx$

$\int g'(x) f'(g(x)) \; dx = f(g(x))$

反链式看不出来的话，可以使用变量代换

定积分性质：

$\int _a ^b f(x) dx + \int _b ^c f(x) dx = \int _a ^c f(x) dx$

$\int _a ^a f(x) dx = 0$

$\int _a ^b f(x) dx = - \int _b ^a f(x) dx$

$\text{if } f(x) \leqslant g(x) \text{ then } \int _a ^b f(x) dx \leqslant \int _a ^b g(x) dx \qquad (a<b)$

微分应用--微分方程

微分方程：包含微分的方程称为微分方程

注意：传统方程的解是一个数字，微分方程的解是一个函数

例1

$(\frac{d}{dx} + x)y=0$

$\frac{dy}{y}=-x dx$

$\int \frac{1}{y} dy = \int -x dx$

$\ln y = - \frac{1}{2} x^2 + C$

$e^{\ln y} = e^{-\frac{1}{2}x^2 + C}$

$y = A e^{-\frac{1}{2} x^2} \quad (A=e^C)$

例2

4.1. 如何理解定积分

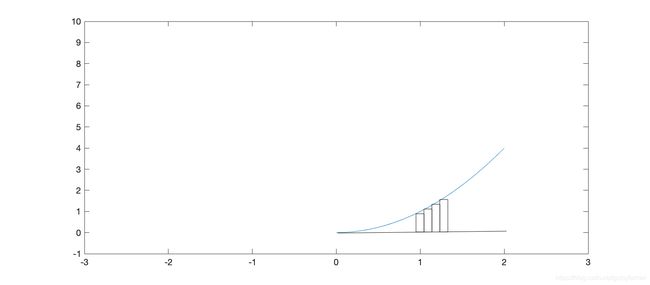
定积分有多种理解方式，其中一种就是“曲线下的面积”

$\text{area} = \int _a ^b f(x) dx$

从几何上讲，积分只是“对许多宽很小的矩形面积求和”，精确地说，x 轴上方的面积减去 x 轴下方的面积

导函数曲线下的面积等于原函数两个函数值的差，因此可以利用积分求曲线下的面积：

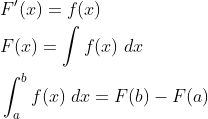
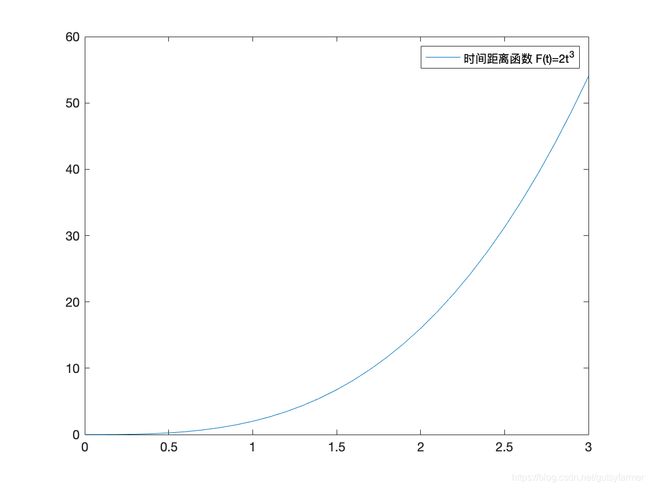
通过“时间距离方程”可以说明为什么曲线下的面积等于原函数两个值的差：

假设“时间距离方程”及其导函数“时间速率方程”为：

$\begin{align*} & F(t) = 2t^3 \\ & F'(t) = f(t) = 6t^2 \end{align*}$

通过“时间距离方程”求1秒到2秒经过的距离：

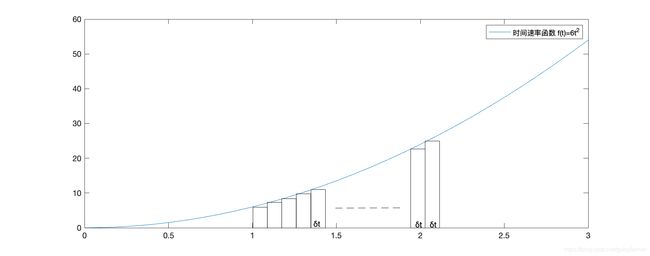
通过“时间速率方程”求1秒到2秒经过的距离：

$distance = f(1) * \Delta t + f(1+\Delta t) * \Delta t + f(1+ 2\Delta t) * \Delta t + \cdots$

当δt趋于0时，通过“时间速率方程”求得的距离近似等于“时间距离方程”的结果。

又因为：

$f(1)*\Delta t, f(1+ \Delta t)*\Delta t, \cdots$

为导函数曲线下的一系列长方形的面积，因此如果想求某个曲线下的面积，可以先对曲线积分，然后利用积分求得曲线下的面积

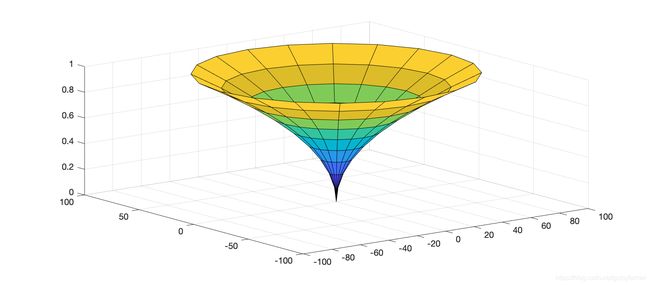
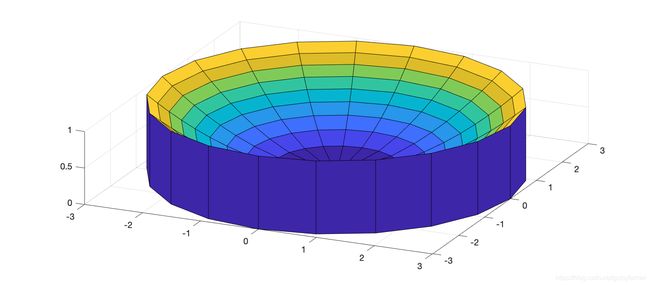
进一步扩展，可以利用积分思想求旋转体的体积(圆盘方法，壳方法)。

假设导函数沿x轴旋转，旋转体的体积（圆盘方法）为：

$\begin{align*} & A=\pi (f(x))^2 \\ & V_d = \pi (f(x))^2 \; dx \\ & V_t = \int \pi (f(x))^2 \; dx \end{align*}$

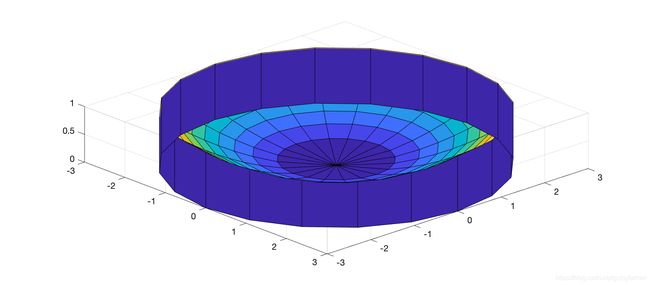
假设导函数沿y轴旋转，旋转体的体积（壳方法）为：

$\begin{align*} & C = 2 \pi r = 2 \pi x_1 \\ & A = C \cdot h = 2 \pi x_1 \cdot f(x_1) \\ & V_{shell} = A \cdot dx = 2 \pi x_1 \cdot f(x_1) \cdot dx \\ & V_t = \int 2 \pi x f(x) dx \end{align*}$

4.2. 例子

4.2.1. 换元法

$\int (\sin x)^3 \; \cos x \;dx$

$let \quad u=\sin x , \quad \frac{du}{dx}=\cos x$

$\int (\sin x)^3 \; \cos x \; dx = \int u^3 \frac{du}{dx} dx = \int u^3 du = \frac{1}{4} u^4 = \frac{1}{4} (\sin x)^4$

4.2.1.1. 三角换元法

三角换元法隶属于换元法

$\int \frac{1}{\sqrt{3 - 2x^2}} \; dx = \int \frac{1}{\sqrt{3(1-\frac{2}{3}x^2)}} \; dx$

$set \quad \frac{2}{3} x^2 = (\sin \theta)^2$

$\Rightarrow \theta = \arcsin \sqrt{\frac{2}{3}} \; x$

$x = \sqrt{\frac{3}{2}} \sin \theta \qquad \frac{dx}{d \theta} = \sqrt{\frac{3}{2}} \cos \theta$

$\begin{align*} & \int \frac{1}{\sqrt{3(1-\frac{2}{3} x^2)}} \; dx \\ & = \int \frac{\sqrt{\frac{3}{2}} \cos \theta \; d \theta}{\sqrt{3(1- (\sin \theta)^2)}} \\ & = \int \frac{\sqrt{\frac{3}{2}} \cos \theta \; d \theta}{\sqrt{3} \cos \theta} \\ & = \frac{1}{\sqrt{2}} \; \theta + C \end{align*}$

将Θ代回去：

$\frac{1}{\sqrt{2}} \theta + C = \frac{1}{\sqrt{2}} \arcsin \sqrt{\frac{2}{3}} x + C$

例2：

$\int \sin^m x \cos^n x dx$

根据 m,n 奇偶的情况，计算方法不同

4.2.2. 分部积分

$\int e^x \cos x \; dx = \frac{e^x \sin x + e^x \cos x}{2}$

证明：

$assume \quad f(x) = e^x, \quad g'(x) = \cos x$

$\int e^x \cos x \; dx = e^x \sin x - \int e^x \sin x \; dx$

$assume \quad f(x) = e^x, \quad g'(x) = \sin x$

$\begin{align*} \int e^x \cos x \; dx &= e^x \sin x - \int e^x \sin x \; dx \\ &= e^x \sin x - (e^x \cdot -\cos x - \int (e^x \cdot -\cos x) dx ) \\ &= e^x \sin x + e^x \cos x - \int e^x \cos x \; dx \\ 2 \int e^x \cos x \; dx &= e^x \sin x + e^x \cos x \\ \int e^x \cos x \; dx &= \frac{e^x \sin x + e^x \cos x}{2} \end{align*}$

5. 微积分第一定理

$\int _a ^b f(x) dx = F(b) - F(a)$

该式子又称为微积分第一定理

应用：求曲线长度，曲线下的面积，体积，平均值(离散平均值，连续平均值，加权平均值)，概率等；直线，圆等的长度都可以用微积分思想来求

例1：

离散平均值 -> 连续平均值

$\frac{y_1 + y_2 + \cdots + y_n}{n} \rightarrow \frac{1}{b-a} \int _a ^ b f(x) dx$

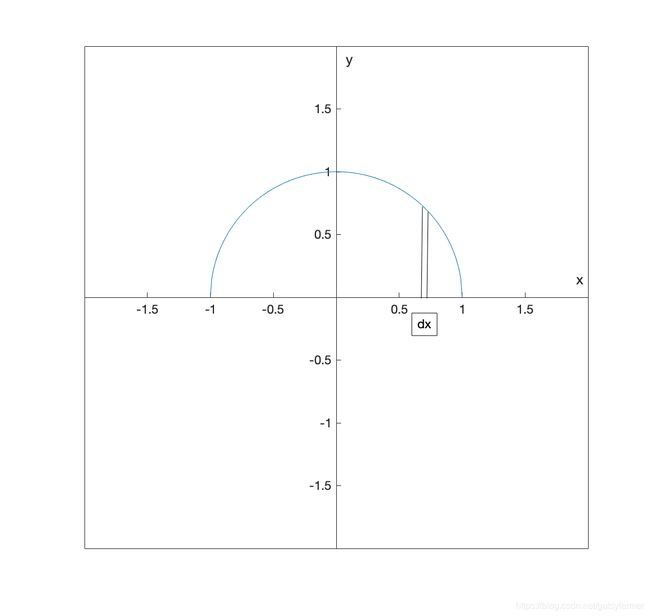
比如点在半圆上的平均高度（对 dx 计算平均值）：

$\text{continuous average} = \frac{1}{1 - (-1)} \int _{-1} ^1 \sqrt{1-x^2} dx = \frac{\pi}{4}$

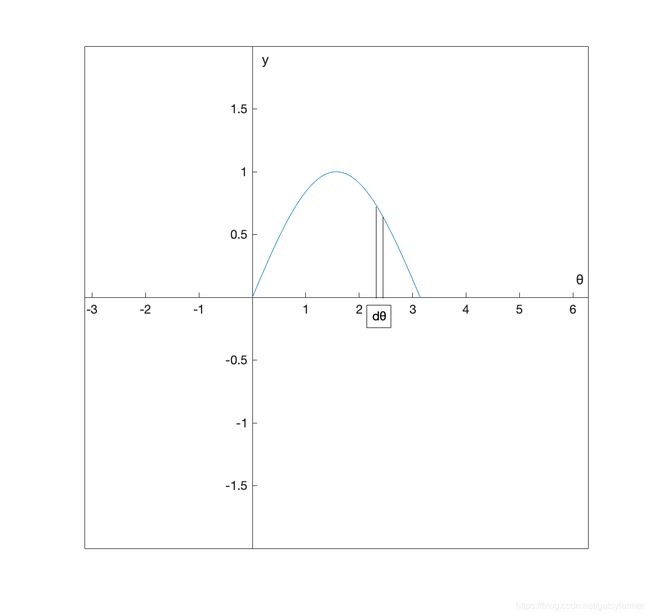
另一种平均高度（对 dθ 计算平均值）：

$\text{continuous average} = \frac{1}{\pi} \int _0 ^{\pi} \sin \theta d \theta$

例2：

加权平均值（weighted average）

$\text{weighted average} = \frac{\int _a ^ b f(x) w(x) dx}{\int _a ^ b w(x) dx}$

解释1：假设 f(x)=C ，分母必须等于权重的积分

解释2：假设第一次买某股票的价格为 f1，买了 w1 股，第二次价格为 f2，买了 w2 股，依次类推，买股票的平均价格为：

$\text{weighted average} = \frac{f_1 w_1 +f_2 w_2 + \cdots + f_n w_n }{w_1 + w_2 + \cdots + w_n}$

例3：

数值积分：黎曼和、梯度法、辛普森公式

如何将问题演变成数学问题？

很多概率问题都符合：

$P = C e^{-r^2}$

5.1 微积分第一定理与中值定理的比较

$\text{let } \Delta F = F(b)-F(a)= \int _a ^b f(x) dx , \qquad \Delta x = b - a$

$\frac{\Delta F}{\Delta x} = \frac{1}{b-a} \int _a ^b f(x) dx = Ave(f)$

$\Delta F = Ave(F') \Delta x$

要想理解 Ave(f) ，可以假设积分时 dx 的宽度为1，然后从离散值求平均的概念进行理解

而中值定理为：

$\Delta F = F'(c) \Delta x$

其中，c 在定义域内是不确定的，只知道 a < c < b，也就是说不知道 c 究竟是哪一点，它比较笼统和简单

而 Ave(F') 是确定值，因此微积分基本定理比中值定理“强”，只要能用积分，就应尽量避免使用中值定理

6. 微积分第二定理

$\text{If f is continuous and } G(x) = \int _a ^x f(t) dt; a \leqslant t \leqslant x$

$\text{then } G'(x) = f(x)$

$G'(x) = \frac{d}{dx} \int _a ^x f(t) dt = f(x)$

微积分第二定理的意思是，一个函数能够找到其相应的积分形式

当一个函数由上述积分形式给出时，先通过其一阶、二阶导数作图，因为了解一个函数，最直观的办法就是画图

证明：

应用：解微分方程

例1：

$y' = \frac{1}{x} \qquad \Rightarrow \qquad L(x) = \ln \left | x \right |$

但 L(x) 的积分形式为：

$L(x) = \int _1 ^ x \frac{1}{t} dt$

例2：

$\text{assume } F(x) = \int _0 ^x e^{-t^2} dt$

$F'(x) = e^{-x^2} \text{ and } F(0)=0$

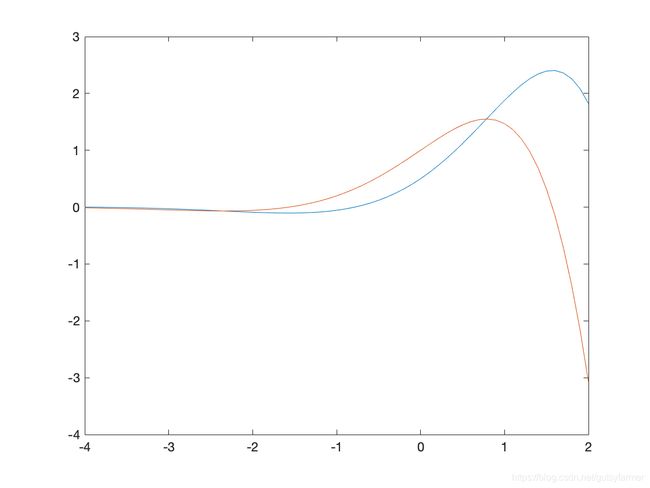
F' 为有名的钟形曲线 bell curve，它是从概率论得出的（概率就是部分与整体的比值）；F(x) 则为 F' 曲线下的面积

由数值 $\frac{ \sqrt \pi}{2}$ ，数学家又引入了一个新的函数--误差函数：

$\text{erf}(x) = \frac{2}{\sqrt \pi} F(x) = \frac{2}{\sqrt \pi} \int _0 ^x e^{-t^2} dt$

你可能感兴趣的:(公开课,可汗学院,微积分)

准备胡珊珊乐平九小
尊敬的各位领导、各位同仁们：大家上午好！我是来自乐平九小的胡珊珊。今天很高兴能有机会给大家做“智慧作业”应用培训。说到“智慧作业”我感触颇多，我是在智慧作业中成长起来的，我也时常以自己是一名“智慧作业人”自居。早在2020年疫情期间，学校电教处周光杰主任在学校群里发出智慧作业抢题通知，我看了有些心动，一节微课相当于一次省级公开课，这对于我们普通老师是多么难得的机会啊。但想归想，我也不会用软件啊，再
经济金融学公开课学习总汇（九）佳佳爱科技AITech
本章内容：1.什么是金融风险2.什么是风险偏好与满意度，人都是风险厌恶吗3.单一投资还是多元投资4.无差别曲线金融风险：金融风险是指金融变量的各种可能值偏离期望的可能性以及幅度，所以风险不是说，一定会发生概率的亏损或者偏离回报，它也有可能发生超额的回报作为理财的投资人，我们一般只关注系统风险（经济环境不好造成房市大跌等）。还有非系统性风险（购买理财，卷款跑路等）。其中系统风险是可分散的风险；后者是
如何有效的学习AI大模型？ Python程序员罗宾学习人工智能语言模型自然语言处理架构
学习AI大模型是一个系统性的过程，涉及到多个学科的知识。以下是一些建议，帮助你更有效地学习AI大模型：基础知识储备：数学基础：学习线性代数、概率论、统计学和微积分等，这些是理解机器学习算法的数学基础。编程技能：掌握至少一种编程语言，如Python，因为大多数AI模型都是用Python实现的。理论学习：机器学习基础：了解监督学习、非监督学习、强化学习等基本概念。深度学习：学习神经网络的基本结构，如卷
公开课，是选择学生的心灵，还是社会的好评？文明未央
远方，还有一缕阳光大教育家李镇西，在上完公开课后进行了一个反思，他说，“公开课是为了自己教学的完美而无视学生的精神自由，让学生成为自己表演的道具。而这样的教育，难道是我们应该提倡的吗？在学生的心灵与社会的评价之间，我们究竟该选择什么？”这里需要说明的是，学生的心灵，指的是最纯粹的、本真的、原生态呈现的语文教学效果，是真善美的有效结合，即使不完美，但也是课堂最真实的生成。社会的评价，指的是教育专家、
周末小事林溪留痕
在学校待了两天，总算是把课件搞了个差不多，床单被罩也都洗了。虽然这周没回去，但是还是做了事情的。明天争取多练习几遍要讲的内容，争取做到烂熟于心，来应付后天的公开课，不管最后结果怎么样，总之，我觉得自己尽力了，最起码自己不会后悔。生活就是这样啊，欢快的时间总是那么短暂，接下来又迎来了新的一周，又有新的磨难，每天都有新的挑战，累是真的，偶尔有点快乐也是真的。愿明天的阳光依然灿烂，今天晒过被子的我，阳光
2.0第一周检视（8/16-8/20） aeb1fe80c479
目标一：早起6:30目标二：运动每周3次以上（跑步，跳绳，瑜珈，冥想，快/慢走10000步……）目标三：早睡23点1.健康：本周精力感觉不足，总是犯困，每天也23点睡觉早上6点多会醒，但是醒来后还是感觉困，睡眠软件记录深眠只有1小时左右，午休做10分钟冥想补充精力；运动：两次美姿雅仪锻炼，一次晚上快走1W+2.学习：上了叶老师的财富公开课和PPT公开课发现有上海班，立即决定预约10月PPT3.线下
公开课悉数沉淀w
果果焦点解决网络中十五坚持分享第1165天2022.4.11累，谁不累啊！上好公开课是一个教师教学能力的重要体现，是评各级名师、学科骨干教师、学科带头人的重要依据，也是职评考核重要指标。最近笔者作为评委，连续听了六十多节一线教师参赛公开课，归纳提炼了上公开课时需要注意十个细节，也可以说要提防的十个坑，旨在对青年教师专业提升有所启迪、帮助。01缺即兴导语，师生情感关联度不够课堂首先是个情感场，然后才
代码随想录算法训练营第三十九天| 62. 不同路径，63. 不同路径 II 零offer在手算法动态规划图论
62.不同路径搞清楚dp[i][j]的定义推导出公式遍历顺序，从左到右，从上到下dp的初始化动态规划中如何初始化很重要！|LeetCode：62.不同路径_哔哩哔哩_bilibili《代码随想录》算法公开课开讲啦！快来打卡！本期视频的文字讲解版在「代码随想录」刷题网站：programmercarl.comGithub：https://github.com/youngyangyang04/leetc
深度学习算法，该如何深入，举例说明 liyy614 深度学习
深度学习算法的深入学习可以从理论和实践两个方面进行。理论上，深入理解深度学习需要掌握数学基础（如线性代数、概率论、微积分）、机器学习基础和深度学习框架原理。实践上，可以通过实现和优化深度学习模型来提升技能。理论深入数学基础线性代数：理解向量、矩阵、特征值和特征向量等，对于理解神经网络的权重和偏置矩阵至关重要。概率论：用于理解模型的不确定性，如Dropout等正则化技术。微积分：理解梯度下降等优化算
书法心语仙泉
书法，对于我来说就是一个梦中情人。心仪已久，却难以企及。所谓伊人，在水一方。书法就是诗经里那个神秘的“伊人”。为什么我总也抓不住她呢？因为，一直没有找到真正接触她的渠道，仅靠我的暗恋，无法得到她的芳心。2016年之夏，某天我在住家附近走路，突然在街道边看到了“北京盛世兰亭书院”书法公开课的宣传海报。于是我记住了日子，在一个星期天到场听了书法课。我一下子像触电了，觉得禅宗所谓的“开悟”时刻到了。没有
C语言深入了解指针一(14) tan180° C c语言
文章目录前言一、内存和地址内存究竟该如何理解编址二、指针变量和地址取地址操作符&解引用操作符*指针变量的大小总结前言终于来到指针啦！如前篇末尾总结所说，这是你们马上要下大功夫的地方但是，就像我们上初中的时候，有人说函数难；我们上高中的时候，有人说导数、圆锥难；上大学的时候，有人说微积分难，事实上，别被吓到了，先勇敢尝试，迈过去了也就那么回事~一、内存和地址脱离内存和地址讲指针就是耍流氓！内
《兴奋的睡不着》坚持第922天原创分享（2017.06.17星期六）半夏五月天
《兴奋的睡不着》卓丽，坚持第922天原创分享（2017.06.17星期六）：刘老师要来平顶山了，我们平顶山焦点团队的各位老师都开心的不得了，刘老师还特意给我们带来一节公开课，这是多么难得的机会呀，由于场地有限，只能小范围的通知，可是依然挡不住的热情，仅仅一天时间就截止报名了。我们下午四点就开始布置会场，由于来的人多，我们又去借凳子，大家也都早早来占位，都在等待着激动人心的那一刻。刘老师路上耽搁，依
非理工科院校怎么打好数学建模比赛 | 南川笔记南川笔记
Proposition1非理工科院校最好不要打数学建模比赛。虽说“一次建模，终身受益”，但毕竟数学建模既要数学理论的支撑（不仅仅是大学里的微积分、线性代数和概率论与统计，更多的是基于微积分的常偏微分方程、基于线性代数的运筹学和基于概率论与统计的统计分析内容），还要编程的支撑（不是常规的C语言或者Java程序，也不是这几年很火的Python编程，而是基于数值运算的Matlab和基于统计的R），这在一
微积分在神经架构搜索中的应用光剑书架上的书深度强化学习原理与实战元学习原理与实战计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
微积分在神经架构搜索中的应用1.背景介绍随着深度学习技术的飞速发展,神经网络模型的复杂度也在不断提高,从最初的简单全连接网络,到如今的卷积神经网络、循环神经网络、注意力机制等各种复杂的神经网络架构。这些先进的神经网络架构大大提高了深度学习模型的性能,但同时也给神经网络的设计和调优带来了巨大的挑战。手工设计神经网络架构通常需要大量的专业知识和经验积累,过程繁琐复杂,难以推广。为了解决这一问题,神经架
记忆力培训与记忆课乌卓
昨天老徐拉我进了记忆公开课的群，研究了课程助理的工作流程之外，也读了群里提到的那本《世界记忆大师教我的超强记忆法》。先说一下这本书，看了前面一小半，联想记忆。联想记忆包括形象联想、谐音联想、夸张联想、运动联想、代替联想。也就是说，要训练好记忆力，就要把见到的陌生的信息联想成自己脑子里熟悉的信息，通过夸张之类的方法，把信息在脑子里刻下印记，因为我们的大脑对新奇的事物总会印象深刻。今天不写书评，因为我
终于结束了有一种夹心叫中国心
心都快提到嗓子眼里了一大早起床躺在床上还在想课，顺流程脑子里一遍一遍的过，一句一句的顺词本来已经参加过好几次的公开课了青年教师必修课可是这次我却不幸排在了第一个讲让我从知道安排之后一直都在准备每天睁眼就在想怎么办周六日也在备课我的师傅是一个很有教学经验，也很有活力的一位老师临到昨天她还在耐心的帮我指导我需要改进的地方，我特别感激其实她也可以不管我，讲成什么算什么可是我运气真的很好，遇到这么认真负责
C语言知识点完美总结哪有岁月静好
C语言最重要的知识点总体上必须清楚的:1)程序结构是三种:顺序结构、选择结构(分支结构)、循环结构。其实做为一个开发者，有一个学习的氛围跟一个交流圈子特别重要这里我推荐一个C语言C++交流群583650410，不管你是小白还是转行人士欢迎入驻，大家一起交流成长。免费的公开课供你学习！2)读程序都要从main()入口,然后从最上面顺序往下读(碰到循环做循环,碰到选择做选择)，有且只有一个main函数
随心小记君怡w
这几天大概都只能写“随心小记”啦，最近实在是有些忙，忙得我也没有什么特别的思考，就随心写些日常，记录一下平凡的生活吧。我的自律怕是在大学以前都耗尽了吧，今天计划好六点40起床，找个自习室学微积分的，结果早晨把闹钟调掉后再醒来已是中午。我赶紧起床，另一个舍友还在床上，我便帮她去食堂带了饭，然而回来的路上下雨了，我既没有伞也没有帽子，只能一路低头淋雨小跑回来。刚刚坐下还没来得及吃饭，班长又来催我们把外
2023-10-16 静待花开1975
感觉今天好忙啊，似乎一刻也没闲着，上午上完课就开始弄知识清单，下午一上班就开始改作业，然后上课、开会，忙到快九点了才下班。明天就要上公开课了，不知道为啥，一点感觉都没有，明明还没准备好呢，却硬是不紧张也不慌乱，大概是这几年被否定的太多，随波逐流，混成油条了吧。下午同事说起一件事，她看我在班里搞图书角，也想做，却直接被班主任否定了。理由是：别玩花样，把成绩提上去才是硬道理。我听了有些难过，让学生多读
盘点一下2019年互联网都发生了哪些大事件测试帮日记
点击链接加入QQ群138269539（全国招聘信息、免费公开课、视频应有尽有）：https://jq.qq.com/?_wv=1027&k=5q0IklJ更多内容可以关注公众号：测试帮日记2019年对许多人来说太难了，尤其是对互联网行业从业者来说，有这样一段话：“2019年可能是过去十年中最糟糕的一年，但却是未来十年中最好的一年。”来来来，让我们回顾一下今年都发生了哪些重大事件：锤子卖了，老罗换了
2022-01-03 梵兮瑜伽洛洛老师
今天邀约：3办卡：0早上上了一节私教1.吴思捷麻麻：推了次卡明天跟进2.吴清柳觉得没有难度3.贺芬参观了明天再来打电话20邀约公开课：4明天邀约：4个黄雪英潘德桃徐子淇贺芬老会员接待1个考虑升级
心累我在枣快乐呀
这个点才洗漱完毕，10点才回到宿舍，莫名心累，觉得时间真的太浪费了。下午4点多才出发桥头，唉，一些所谓的“交流”，时间全花在路上和听“废话”上。最近开放日，加上考试，一大堆杂七杂八的事情，明天上午去听课，下午磨课，级部还要检查环境，周三上午公开课，周四开始月考，莫名心累，如果有那么些瞬间真的想什么岗位都不要，就安安静静地在当一名幸福的班主任，备好课，上好课，教好学生。大家都不容易，刘主任说回到后还
求笛卡尔系数在第二象限的曲面微积分的吹牛逼函数两碗豆浆
图片发自App最近有些嘚瑟，想着写一些好玩的东西，来记录自己思考的一点一滴，但是愚钝如我，每到落笔时才发现，一时念头和落到文字完全不是一回事。至于写的东西，我也在尽力避免自己以前写的思考和肤浅，因为如果执着于以前，那势必还是在原地踏步，想着在原来不成熟的基础上，尽可能得到一些新的发现和思考，以求得自己能够有一点变化。————题目这么起，是因为最近看笛卡尔的书启发了一些东西，然后这几天也一直在私下里
中原焦点网初第34期坚持分享第19天2022.4.24 爱尚教育
本周复盘这周有哪些进步？最希望下一周有哪些变化？这周有哪些进步？1.完成了人人献课、健全人格公开课、学科课题化献课，三课整合的公开课研讨活动，探索了以任务为导向，以问题为驱动，以小组合作的实践探究的课堂教学模式。2.完成了写作分享第19天，每天早上六点起床，健康运动，愉快阅读，有序规划。每天一点点，也许看不到多大变化，但是坚信你一定在发生着变化。最希望下周有哪些变化？1.关注身体：每晚泡脚，每天运
做一个学生喜欢的数学老师 a修娟
在双语工作多年，习惯了每天忙忙碌碌的生活和工作的快节奏，在累和忙碌的同时也收获着幸福和快乐，因为我心中有一个信念，那就是：做一个学生喜欢的数学教师。经常看到，优秀的老师们上公开课前师生交流，不是和学生谈话、提问，就是和学生一起做游戏等,他们的目的其实很简单，那就是让学生喜欢上你这个老师，从而喜欢上你的数学课。大家都知道数学课是枯燥无味的，如何让学生喜欢上数学课，是摆在每位数学教师面前的一个很值得思
【62】关于上公开课《金色的草地》有感邓维_ca53
上周五上了一节公开课选自课文《金色的草地》第二课时。一开始学校安排上公开课，我第一感觉是选了这篇课文，纯粹是因为喜欢蒲公英，真的是跟着感觉。后来仔仔细细研究了一下，发现这篇课文还真不是那种被挑出来做可以标准化流程或者有代表性的课文做公开课选材。既然如此那我就走走不寻常的路线。我不适合讲特别讲究细节没有哲学味道的课文！我很喜欢跟学生去聊一些比较深的东西，骨子里想脱离课文，去跟他们说一说圈子外的东西。
Day 18 既要仰望星空，也要脚踏实地南和038胡媛媛
已经有三天没有更文了，今天上午的培训强度不是很大，听完两节公开课，简单地来回顾一下这几天的培训内容。28号上午上完两个班的课，安排好班里面的各种事情，中午简单吃过午饭开车来到邢台学院聆听了徐燕坤老师和张校长给我们分享的关于手绘版和电脑版的思维导图的制作。其实思维导图一直是我特别感兴趣的一个研究方向，在我们的课程当中我们可以运用思维导图让孩子们理清头绪，从而把握语言点、把握语法结构以及其它我们需要讲
2021-09-25 做个会思考的老师
又要讲公开课了，一如既往地要紧张一段时间。这种感觉可能每个老师都会有吧，站在讲台上已经21年了，大大小小的公开课也讲了不少，可每次要开公开课，还是会这样紧张。紧张，说明自己对课堂有敬畏。站在课堂上，我们就代表了这个学科，这节课我们能带给孩子们一些什么呢？知识的增长，方法的掌握、能力的提升、还是思维的培养？新课程理念下的课堂，仿佛对一节课提出了很多的要求，我们也总想把一节课塞的满满的，似乎这样才能显
记第一次录课半亩方塘点点香
2018年，我有幸走上了教师岗位，从此成为了一名语文老师兼班主任。第一年，自知自己不会讲课和教学，再说，一年级的小豆豆，还是不要带出去挑战的好！第二年，一到公开课，录课的老师特别多，再加上录课教室座位有限，多余的孩子总是没处安排，我从来没有录过课。今年，已经迈入第三年了。说起来要感谢大队部安排的这次活动，也要感谢各位办公室班主任放弃了，让我有机会做一次公开队会课，也算是开启了第一次录课。今天队会的
线性代数-MIT 18.06-6(a) 儒雅的钓翁数学基础线性代数矩阵机器学习
文章目录26.对称矩阵及正定性对称矩阵对称矩阵的特性：矩阵分解（谱定理）定理证明和复数推广对称矩阵和投影矩阵正定性性质1性质227.复数矩阵和快速傅里叶变换复数向量复数矩阵对称性正交性傅里叶矩阵快速傅里叶变换本文在学习《麻省理工公开课线性代数MIT18.06LinearAlgebra》总结反思形成视频链接：MITB站视频笔记部分：总结参考子实26.对称矩阵及正定性对称矩阵对称矩阵的特性：特征值为实
矩阵求逆（JAVA）利用伴随矩阵 qiuwanchi 利用伴随矩阵求逆矩阵
package gaodai.matrix; import gaodai.determinant.DeterminantCalculation; import java.util.ArrayList; import java.util.List; import java.util.Scanner; /** * 矩阵求逆(利用伴随矩阵) * @author 邱万迟
单例（Singleton）模式 aoyouzi 单例模式 Singleton
3.1 概述如果要保证系统里一个类最多只能存在一个实例时，我们就需要单例模式。这种情况在我们应用中经常碰到，例如缓存池，数据库连接池，线程池，一些应用服务实例等。在多线程环境中，为了保证实例的唯一性其实并不简单，这章将和读者一起探讨如何实现单例模式。 3.2
[开源与自主研发]就算可以轻易获得外部技术支持,自己也必须研发 comsci 开源
现在国内有大量的信息技术产品，都是通过盗版，免费下载，开源，附送等方式从国外的开发者那里获得的。。。。。。虽然这种情况带来了国内信息产业的短暂繁荣，也促进了电子商务和互联网产业的快速发展，但是实际上，我们应该清醒的看到，这些产业的核心力量是被国外的
页面有两个frame,怎样点击一个的链接改变另一个的内容 Array_06 UI XHTML
<a src="地址" targets="这里写你要操作的Frame的名字" />搜索然后你点击连接以后你的新页面就会显示在你设置的Frame名字的框那里 targerts="",就是你要填写目标的显示页面位置 ===================== 例如： <frame src=&
Struts2实现单个/多个文件上传和下载 oloz 文件上传 struts
struts2单文件上传：步骤01:jsp页面  　　<form action="fileUplo
推荐10个在线logo设计网站 362217990 logo
在线设计Logo网站。 1、http://flickr.nosv.org（这个太简单） 2、http://www.logomaker.com/?source=1.5770.1 3、http://www.simwebsol.com/ImageTool 4、http://www.logogenerator.com/logo.php?nal=1&tpl_catlist[]=2 5、ht
jsp上传文件香水浓 jsp fileupload
1. jsp上传 Notice： 1. form表单 method 属性必须设置为 POST 方法，不能使用 GET 方法 2. form表单 enctype 属性需要设置为 multipart/form-data 3. form表单 action 属性需要设置为提交到后台处理文件上传的jsp文件地址或者servlet地址。例如 uploadFile.jsp 程序文件用来处理上传的文
我的架构经验系列文章 - 前端架构 agevs JavaScript Web 框架 UI jQuer
框架层面：近几年前端发展很快，前端之所以叫前端因为前端是已经可以独立成为一种职业了，js也不再是十年前的玩具了，以前富客户端RIA的应用可能会用flash/flex或是silverlight，现在可以使用js来完成大部分的功能，因此js作为一门前端的支撑语言也不仅仅是进行的简单的编码，越来越多框架性的东西出现了。越来越多的开发模式转变为后端只是吐json的数据源，而前端做所有UI的事情。MVCMV
android ksoap2 中把XML(DataSet) 当做参数传递 aijuans android
我的android app中需要发送webservice ，于是我使用了 ksop2 进行发送，在测试过程中不是很顺利,不能正常工作.我的web service 请求格式如下 [html] view plain copy <Envelope xmlns="http://schemas.
使用Spring进行统一日志管理 + 统一异常管理 baalwolf spring
统一日志和异常管理配置好后，SSH项目中，代码以往散落的log.info() 和 try..catch..finally 再也不见踪影！统一日志异常实现类： [java] view plain copy package com.pilelot.web.util; impor
Android SDK 国内镜像 BigBird2012 android sdk
一、镜像地址： 1、东软信息学院的 Android SDK 镜像，比配置代理下载快多了。配置地址， http://mirrors.neusoft.edu.cn/configurations.we#android 2、北京化工大学的： IPV4:ubuntu.buct.edu.cn IPV4:ubuntu.buct.cn IPV6:ubuntu.buct6.edu.cn
HTML无害化和Sanitize模块 bijian1013 JavaScript AngularJS Linky Sanitize
一.ng-bind-html、ng-bind-html-unsafe AngularJS非常注重安全方面的问题，它会尽一切可能把大多数攻击手段最小化。其中一个攻击手段是向你的web页面里注入不安全的HTML，然后利用它触发跨站攻击或者注入攻击。考虑这样一个例子，假设我们有一个变量存
[Maven学习笔记二]Maven命令 bit1129 maven
mvn compile compile编译命令将src/main/java和src/main/resources中的代码和配置文件编译到target/classes中，不会对src/test/java中的测试类进行编译 MVN编译使用 maven-resources-plugin:2.6:resources maven-compiler-plugin:2.5.1:compile &nbs
【Java命令二】jhat bit1129 Java命令
jhat用于分析使用jmap dump的文件，，可以将堆中的对象以html的形式显示出来，包括对象的数量，大小等等，并支持对象查询语言。 jhat默认开启监听端口7000的HTTP服务，jhat是Java Heap Analysis Tool的缩写 1. 用法： [hadoop@hadoop bin]$ jhat -help Usage: jhat [-stack <bool&g
JBoss 5.1.0 GA:Error installing to Instantiated: name=AttachmentStore state=Desc ronin47
进到类似目录 server/default/conf/bootstrap，打开文件 profile.xml找到： Xml代码<bean name="AttachmentStore" class="org.jboss.system.server.profileservice.repository.AbstractAtta
写给初学者的6条网页设计安全配色指南 brotherlamp UI ui自学 ui视频 ui教程 ui资料
网页设计中最基本的原则之一是，不管你花多长时间创造一个华丽的设计，其最终的角色都是这场秀中真正的明星——内容的衬托我仍然清楚地记得我最早的一次美术课，那时我还是一个小小的、对凡事都充满渴望的孩子，我摆放出一大堆漂亮的彩色颜料。我仍然记得当我第一次看到原色与另一种颜色混合变成第二种颜色时的那种兴奋，并且我想，既然两种颜色能创造出一种全新的美丽色彩，那所有颜色
有一个数组，每次从中间随机取一个，然后放回去，当所有的元素都被取过，返回总共的取的次数。写一个函数实现。复杂度是什么。 bylijinnan java 算法面试
import java.util.Random; import java.util.Set; import java.util.TreeSet; /** * http://weibo.com/1915548291/z7HtOF4sx * #面试题#有一个数组，每次从中间随机取一个，然后放回去，当所有的元素都被取过，返回总共的取的次数。 * 写一个函数实现。复杂度是什么
struts2获得request、session、application方式 chiangfai application
1、与Servlet API解耦的访问方式。 a.Struts2对HttpServletRequest、HttpSession、ServletContext进行了封装，构造了三个Map对象来替代这三种对象要获取这三个Map对象，使用ActionContext类。 -----> package pro.action; import java.util.Map; imp
改变python的默认语言设置 chenchao051 python
import sys sys.getdefaultencoding() 可以测试出默认语言，要改变的话，需要在python lib的site-packages文件夹下新建： sitecustomize.py，这个文件比较特殊，会在python启动时来加载，所以就可以在里面写上： import sys sys.setdefaultencoding('utf-8') &n
mysql导入数据load data infile用法 daizj mysql 导入数据
我们常常导入数据！mysql有一个高效导入方法，那就是load data infile 下面来看案例说明基本语法： load data [low_priority] [local] infile 'file_name txt' [replace | ignore] into table tbl_name [fields [terminated by't'] [OPTI
phpexcel导入excel表到数据库简单入门示例 dcj3sjt126com PHP Excel
跟导出相对应的，同一个数据表，也是将phpexcel类放在class目录下，将Excel表格中的内容读取出来放到数据库中 <?php error_reporting(E_ALL); set_time_limit(0); ?> <html> <head> <meta http-equiv="Content-Type"
22岁到72岁的男人对女人的要求 dcj3sjt126com
22岁男人对女人的要求是：一，美丽，二，性感，三，有份具品味的职业，四，极有耐性，善解人意，五，该聪明的时候聪明，六，作小鸟依人状时尽量自然，七，怎样穿都好看，八，懂得适当地撒娇，九，虽作惊喜反应，但看起来自然，十，上了床就是个无条件荡妇。 32岁的男人对女人的要求，略作修定，是：一，入得厨房，进得睡房，二，不必服侍皇太后，三，不介意浪漫蜡烛配盒饭，四，听多过说，五，不再傻笑，六，懂得独
Spring和HIbernate对DDM设计的支持 e200702084 DAO 设计模式 spring Hibernate 领域模型
A：数据访问对象 DAO和资源库在领域驱动设计中都很重要。DAO是关系型数据库和应用之间的契约。它封装了Web应用中的数据库CRUD操作细节。另一方面，资源库是一个独立的抽象，它与DAO进行交互，并提供到领域模型的“业务接口”。资源库使用领域的通用语言，处理所有必要的DAO，并使用领域理解的语言提供对领域模型的数据访问服务。
NoSql 数据库的特性比较 geeksun NoSQL
Redis 是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库，并提供多种语言的API。目前由VMware主持开发工作。 1. 数据模型作为Key-value型数据库，Redis也提供了键（Key）和值（Value）的映射关系。除了常规的数值或字符串，Redis的键值还可以是以下形式之一： Lists （列表） Sets
使用 Nginx Upload Module 实现上传文件功能 hongtoushizi nginx
转载自： http://www.tuicool.com/wx/aUrAzm 普通网站在实现文件上传功能的时候，一般是使用Python，Java等后端程序实现，比较麻烦。Nginx有一个Upload模块，可以非常简单的实现文件上传功能。此模块的原理是先把用户上传的文件保存到临时文件，然后在交由后台页面处理，并且把文件的原名，上传后的名称，文件类型，文件大小set到页面。下
spring-boot-web-ui及thymeleaf基本使用 jishiweili spring thymeleaf
视图控制层代码demo如下： @Controller @RequestMapping("/") public class MessageController { private final MessageRepository messageRepository; @Autowired public MessageController(Mes
数据源架构模式之活动记录 home198979 PHP 架构活动记录数据映射
hello!架构一、概念活动记录（Active Record）：一个对象，它包装数据库表或视图中某一行，封装数据库访问，并在这些数据上增加了领域逻辑。对象既有数据又有行为。活动记录使用直截了当的方法，把数据访问逻辑置于领域对象中。二、实现简单活动记录活动记录在php许多框架中都有应用，如cakephp。 <?php /** * 行数据入口类 *
Linux Shell脚本之自动修改IP pda158 linux centos Debian 脚本
作为一名 Linux SA，日常运维中很多地方都会用到脚本，而服务器的ip一般采用静态ip或者MAC绑定，当然后者比较操作起来相对繁琐，而前者我们可以设置主机名、ip信息、网关等配置。修改成特定的主机名在维护和管理方面也比较方便。如下脚本用途为：修改ip和主机名等相关信息，可以根据实际需求修改，举一反三！ #!/bin/sh #auto Change ip netmask ga
开发环境搭建独浮云 eclipse jdk tomcat
最近在开发过程中，经常出现MyEclipse内存溢出等错误，需要重启的情况，好麻烦。对于一般的JAVA+TOMCAT项目开发，其实没有必要使用重量级的MyEclipse，使用eclipse就足够了。尤其是开发机器硬件配置一般的人。 &n