算法进阶:聚类算法
文章目录
- 1 聚类算法分类
- 2 常见聚类算法
-
- 2.1 kmeans
-
- 2.1.1 工作原理
- 2.1.2 计算距离的方式
- 2.1.3 kmeans的损失函数
- 2.1.4 k-means算法的优缺点
- 2.2 层次聚类
- 2.3 密度聚类
-
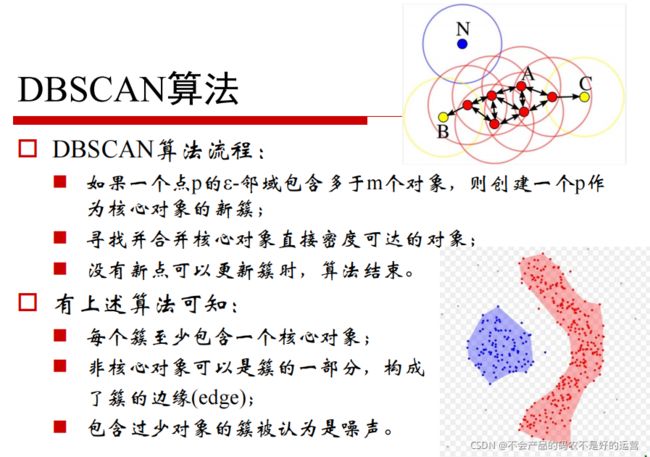
- 2.3.1 DBSCAN
- 2.3.2 密度最大值算法
- 3 聚类算法的模型评估指标
-
- 3.1 当真实标签已知的时候
- 3.2 当真实标签未知的时候:轮廓系数
- 3.3 当真实标签未知的时候:Calinski-Harabaz Index
- 4 sklearn中的调参
-
- 4.1 sklearn.cluster.KMeans
- 4.2 重要参数n_clusters
- 4.3 重要参数init & random_state & n_init:初始质心怎么放好?
- 4.4 重要参数max_iter & tol:让迭代停下来
-
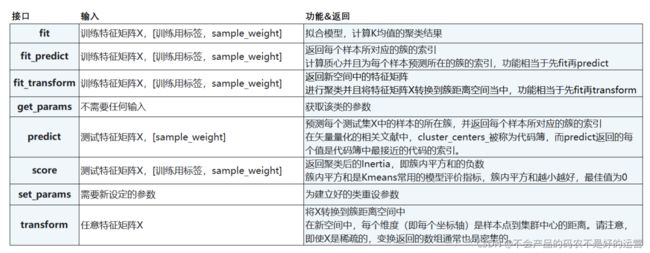
- 4.4.1 重要属性与重要接口
1 聚类算法分类
1、基于划分
给定一个有N个元组或者纪录的数据集,分裂法将构造K个分组,每一个分组就代表一个聚类,K
算法:K-MEANS算法、K-MEDOIDS算法、CLARANS算法
2、层次聚类
对给定的数据集进行层次似的分解,直到某种条件满足为止。具体又可分为“自底向上”和“自顶向下”两种方案。

3、密度聚类
只要一个区域中的点的密度大过某个阈值,就把它加到与之相近的聚类中去。
特点:能克服基于距离的算法只能发现“类圆形”的聚类的缺点。
算法:DBSCAN算法、OPTICS算法、DENCLUE算法
4、谱聚类
谱聚类就是基于图论的聚类方法,通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,从而达到对样本数据的聚类。
具体步骤为:

1、第i个样本和第j个样本度量相似 高斯相似度,其中delta是超参数,svm里面也用到过这个核函数
2、形成相似度矩阵W=(Sij)n*n,对称矩阵,其中sii本来应该等于1,但为了方便计算都写成0,所以相似度矩阵就变长了主对角线上都为0的对称阵。
3、计算第i个样本到其他所有样本的相似度的和di = si1+Si2+…Sin(这里关于Si的相加,有些比如要聚成K类的就只会使用前K个si相加,或者设定一个阈值,小于阈值的si都舍去),在图论中,di叫做度,可以理解为连接边的权值。将所有点的度di,构成度矩阵D(对角阵)
4、形成拉普拉斯矩阵L=D-W,L是对称半正定矩阵,最小特征值是0,相应的特征向量是全1向量。把L的特征值从小到大排列,λ1…λn,对应特征向量u1 u2…un,如果我们要求聚成K类,我们就取前K个特征值对应的特征向量,形成矩阵Un*k,这样我们认为对应第一个样本的特征就是u11,u12…u1k,第二个样本的特征就是u21,u22…u2k,第n个样本的特征就是un1,un2…unn,对这n个样本做K均值,最后对这n个样本的聚类结果是什么,我们原始的聚类结果就是什么。
优点:可以发现非球形的样本
缺点:也要事先给定K值
2 常见聚类算法
2.1 kmeans
2.1.1 工作原理
step1:随机抽取k个样本作为最初的质心
step2:循环:
2.1 将每个样本分到距离他们最近的质心,形成k个簇
2.2 对于每个簇,计算簇内样本的平均值作为新的质心
setp3:当质心的位置不再发生变化,迭代停止,聚类完成
注:当数据量巨大的时候,不用全部样本求均值,选一部分求均值,这种算法称为mini-batch k-means
2.1.2 计算距离的方式
样本点到其所在簇的质心的距离衡量方式有:
令x表示簇中的一个样本点, μ表示该簇中的质心,n表示每个样本点中的特征数目,i表示组成点的每个特征。

余弦距离常用于文本。
如我们采用欧几里得距离,则一个簇中所有样本点到质心的距离的平方和为:

其中,m为一个簇中样本的个数,j是每个样本的编号。这个公式被称为簇内平方和。又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加,就得到了整体平方和。,又叫做total inertia。Total Inertia越小,代表着每个簇内样本越相似,聚类的效果就越好。
2.1.3 kmeans的损失函数
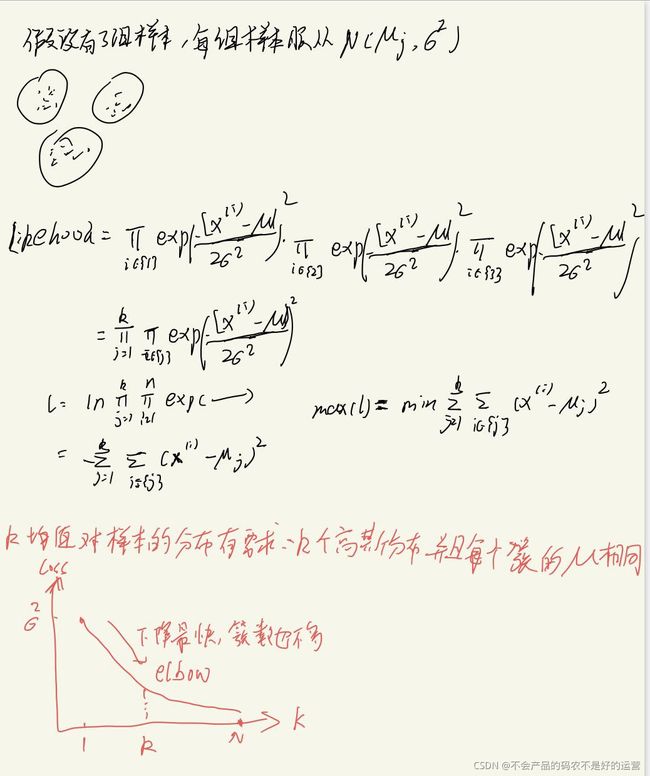
可以说有也可以说没有。我们的目标是求解最小整体平方和所对应的最优质心的位置,整体平方和可以作为损失函数。从下图的推到可以看出,kmeans对样本的分布有要求**:k个高斯分布,并且每个簇的μ相同**
2.1.4 k-means算法的优缺点
2.2 层次聚类
2.3 密度聚类
2.3.1 DBSCAN
2.3.2 密度最大值算法
3 聚类算法的模型评估指标
聚类模型的结果不是某种标签输出,并且聚类的结果是不确定的,其优劣由业务需求或者算法需求来决定,并
且没有永远的正确答案。那我们如何衡量聚类的效果呢?
3.1 当真实标签已知的时候
1、v-measure
取值范围在(0,1)之中,越接近1,聚类效果越好。具体可以细分为均一性和完整性

2、互信息分
取值范围在(0,1)之中
越接近1,聚类效果越好
在随机均匀聚类下产生0分
3、调整兰德系数
取值在(-1,1)之间,负值象征着簇内的点差异巨大,甚至相互独立,正类的
兰德系数比较优秀,越接近1越好
对样本分布没有假设,在任何分布上都可以有不错的表现,尤其是在具有"折叠"形状的数据上表现优秀
在随机均匀聚类下产生0分
3.2 当真实标签未知的时候:轮廓系数
轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的,它能够同时衡量:
1)样本与其自身所在的簇中的其他样本的相似度a,等于样本与同一簇中所有其他点之间的平均距离
2)样本与其他簇中的样本的相似度b,等于样本与下一个最近的簇中的所有点之间的平均距离
根据聚类的要求”簇内差异小,簇外差异大“,我们希望b永远大于a,并且大得越多越好。
单个样本的轮廓系数计算为:
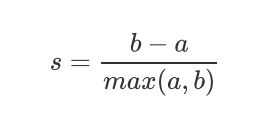
轮廓系数范围是(-1,1),其中值越接近1表示样本与自己所在的簇中的样本很相似,并且与其他簇中的样本不相似,当样本点与簇外的样本更相似的时候,轮廓系数就为负。当轮廓系数为0时,则代表两个簇中的样本相似度一致,两个簇本应该是一个簇。
如果一个簇中的大多数样本具有比较高的轮廓系数,则簇会有较高的总轮廓系数,则整个数据集的平均轮廓系数越高,则聚类是合适的。如果许多样本点具有低轮廓系数甚至负值,则聚类是不合适的,聚类的超参数K可能设定得太大或者太小。
在sklearn中,我们使用模块metrics中的类silhouette_score来计算轮廓系数,它返回的是一个数据集中,所有样本的轮廓系数的均值。但我们还有同在metrics模块中的silhouette_sample,它的参数与轮廓系数一致,但返回的是数据集中每个样本自己的轮廓系数。
3.3 当真实标签未知的时候:Calinski-Harabaz Index
除了轮廓系数是最常用的,还有卡林斯基-哈拉巴斯指数(Calinski-Harabaz Index,简称CHI,也被称为方差比标准)
卡林斯基-哈拉巴斯指数。Calinski-Harabaz指数越高越好。对于有k个簇的聚类而言,Calinski-Harabaz指数s(k)写作如下公式,并且Calinski-harabaz指数越高越好:
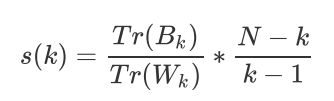
4 sklearn中的调参
4.1 sklearn.cluster.KMeans
class sklearn.cluster.KMeans (n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001,
precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)
4.2 重要参数n_clusters
n_clusters是KMeans中的k,表示着我们告诉模型我们要分几类。这是KMeans当中唯一一个必填的参数,默认为8
类,但通常我们的聚类结果会是一个小于8的结果。通常,在开始聚类之前,我们并不知道n_clusters究竟是多少,因此我们要对它进行探索。
4.3 重要参数init & random_state & n_init:初始质心怎么放好?
初始质心放置的位置不同,聚类的结果很可能也会不一样,一个好的质心选择可以让K-Means避免更多的计算,让算法收敛稳定且更快。一个random_state对应一个质心随机初始化的随机数种子。如果不指定随机数种子,则sklearn中的K-means并不会只选择一个随机模式扔出结果,而会在每个随机数种子下运行多次,并使用结果最好的一个随机数种子来作为初始质心。我们可以使用参数n_init来选择,每个随机数种子下运行的次数。这个参数不常用到,默认10次,如果我们希望运行的结果更加精确,那我们可以增加这个参数n_init的值来增加每个随机数种子下运行的次数。

4.4 重要参数max_iter & tol:让迭代停下来
当质心不再移动,Kmeans算法就会停下来。但在完全收敛之前,我们也可以使用max_iter,最大迭代次数,或者tol,两次迭代间Inertia下降的量,这两个参数来让迭代提前停下来。有时候,当我们的n_clusters选择不符合数据的自然分布,或者我们为了业务需求,必须要填入与数据的自然分布不合的n_clusters,提前让迭代停下来反而能够提升模型的表现。