人工智能之数学基础----连续性和可导性
本章主要讲解函数的联系性,函数的联系性也是导数的必要条件,从而延伸讲解可导性
在一点处及在一个区间上联系
连续函数的零点定理、最值定理、介值定理
平均速度、瞬时速度
切线和导数
二阶导数和高阶导数
在一点上连续
如果
,函数
在点
处连续
假设函数有一个点![]() 的附近是连续【左,右连续】的,这个函数的其它地方不连续没关系,只要在附近连续就可以,总结点上连续;一、点存在,必须有定义,二、附近必须是连续的(也就是左右都要连续);下面是精确的描述
的附近是连续【左,右连续】的,这个函数的其它地方不连续没关系,只要在附近连续就可以,总结点上连续;一、点存在,必须有定义,二、附近必须是连续的(也就是左右都要连续);下面是精确的描述
- 双侧极限
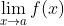 存在(并且是有限的);
存在(并且是有限的); - 函数在点
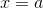 处有定义,即
处有定义,即 存在(并且是有限的)
存在(并且是有限的) - 以上两个量相等,即:
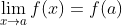
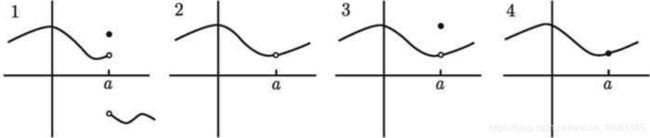
下面我们绘制图像来理解上面的公式
- 图一:虽然在点a有定义,但是左右不连续、左右极限值也不相等,所以不存在双侧极限;
- 图二:左右极限值存在且相等,但是在点a是空心,无定义的,也就是不连续的。
- 图三:双侧极限存在,函数在点
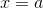 出有定义,但是函数不等于极限值
出有定义,但是函数不等于极限值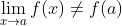
- 图四:双侧极限存在,在
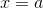 出有定义且连续,且
出有定义且连续,且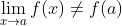 ,所以在点
,所以在点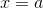 连续
连续
极限分为有限极限和无限极限,什么叫无限极限?例如:
该极限函数是无限极限,随着
函数值将会无限放大,要多大就有多大,没有一个固定的值。什么叫做有限函数呢
该极限函数是有限极限,随着
函数值为0,因为
越大,那么
越小,也就是越接近0,有个固定的值0,所以为有限函数
在区间上连续
- 函数
 在(a,b)总的每一个点都是连续的
在(a,b)总的每一个点都是连续的 - 函数
 在点x=a处右连续,即:
在点x=a处右连续,即: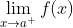 存在(且有限),f(a)存在,并且这两个量相等
存在(且有限),f(a)存在,并且这两个量相等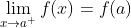
- 函数
 在点x=b处左连接,即:
在点x=b处左连接,即: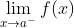 存在(且有限),f(b)存在,并且这两个量相等
存在(且有限),f(b)存在,并且这两个量相等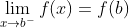
连续函数的零点定理
设函数
在闭区间[a,b]上连续,且
与
异号,那么在开区间(a,b)内至少有一点
使
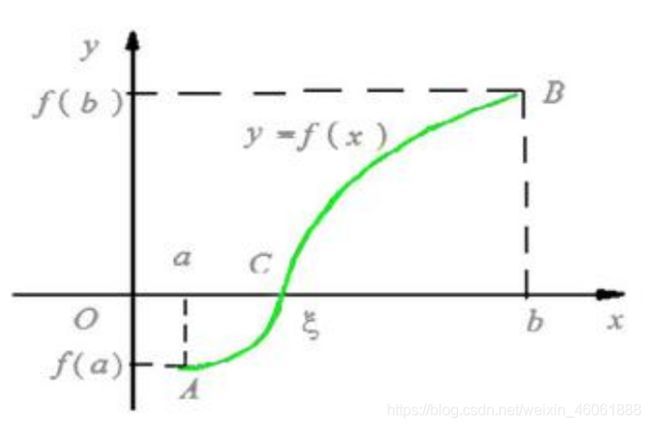 应用:
应用:![]() ,关键在于找到两点
,关键在于找到两点![]() 和
和![]() 是异号,这种题目一般都不需要我们去证明函数的连续性,意思就是连续性是题目已知的,我们只要找到
是异号,这种题目一般都不需要我们去证明函数的连续性,意思就是连续性是题目已知的,我们只要找到![]() 和
和![]() 是异号就可以。
是异号就可以。
连续函数的最值定理
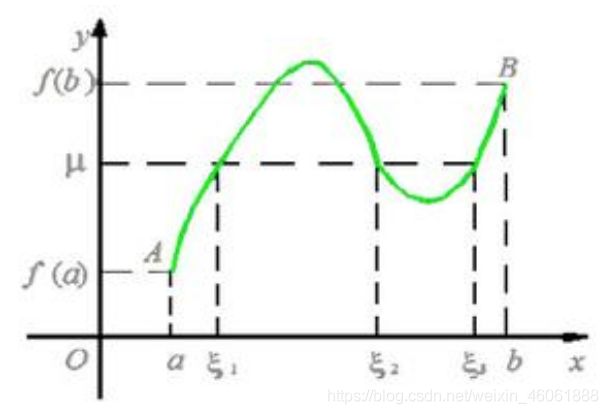 最值定理:若
最值定理:若![]() 在[a,b]上连续,则
在[a,b]上连续,则![]() 在[a,b]上必有最大值和最小值。
在[a,b]上必有最大值和最小值。
介值定理:设函数![]() 在[a,b]上连续,M,m分别为函数在[a,b]上的最大值和最小值,那么对于介于m和M之间的任意一个数C,在闭区间[a,b]内至少有一点
在[a,b]上连续,M,m分别为函数在[a,b]上的最大值和最小值,那么对于介于m和M之间的任意一个数C,在闭区间[a,b]内至少有一点![]() ,使得
,使得![]()
图一:x=c最大值,x=d最小值
图二:x=c最大值,x=a最小值
图三:x=b最大值,x=c=d最小值
图四:每个x都是最大值、最小值
证明三步曲:
- 先找出最值,
 在[a,b]存在M,m
在[a,b]存在M,m - 说明:
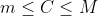
- 利用介值定理:存在
![\xi\in [a,b]](http://img.e-com-net.com/image/info8/3a54ed86fb1d46bda236b1fe6035b75f.gif) ,使得
,使得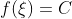 成立
成立
【例一】若![]() 在[a,b]上连续,
在[a,b]上连续,![]()
![]()
![]() 是连续区间,根据最值定理在[a,b]上必然存在最大值M和最小值m
是连续区间,根据最值定理在[a,b]上必然存在最大值M和最小值m
![]() 任意函数
任意函数![]()
平均速度、瞬时速度
发展微积分的最初灵感之一来自于试图去理解运动物体的速度,距离和时间的关系
平均速度=位移/时间
比如我们家里距离上班的地方是10公里,开车需要半个小时,那么我们开车平均速度为每小时20公里;即:(20公里/小时),但是你是无法知道你在公司楼下时候的平均速度的,如果你想知道,你必须在公司楼下这10米,你开车花多长时间。如果这时候有要求知道你在楼下的电线杆旁边的速度,那可能是非常短的距离(可能只有不到1米);如此类推,当距离非常非常短,那么这就是瞬时速度。
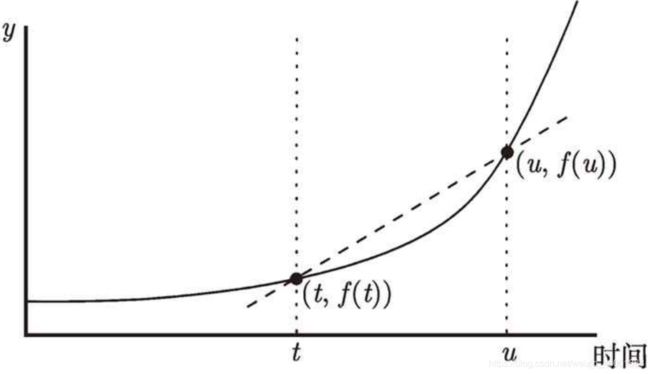
假如我们在不断的缩短![]() 和
和![]() ,也就是让
,也就是让![]() 无限的靠近
无限的靠近![]() ;那么这就是极限
;那么这就是极限![]() ;如下图,瞬时的速率就是求直线的斜率
;如下图,瞬时的速率就是求直线的斜率
当我们的![]() 无限的靠近
无限的靠近![]() 的时候(如下图),令它们的差
的时候(如下图),令它们的差![]() -
-![]() ;即:
;即:![]() ;因为无限靠近,所以
;因为无限靠近,所以![]() 将会不断变小
将会不断变小![]()
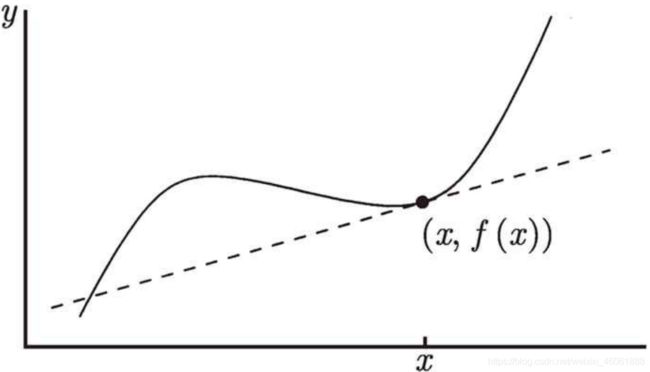 从上图可以看出当
从上图可以看出当![]() 无限的靠近
无限的靠近![]() 的时候,其实就是在求过曲线上某一点求切线的斜率,如左图
的时候,其实就是在求过曲线上某一点求切线的斜率,如左图
导数
【例一】如果![]() ,那么
,那么![]() 是什么?
是什么?
直接套公式
![]()
当最后![]() 可以直接把h去掉
可以直接把h去掉
导数公式的理解与变换
![]() 这里的
这里的![]() 其实是一个变量,是一个无限靠近0的一个变量,我们可以换成其他符号表示,如:
其实是一个变量,是一个无限靠近0的一个变量,我们可以换成其他符号表示,如:![]() ;等价上面的表达式
;等价上面的表达式![]()
由于![]() 是因变量,
是因变量,![]() 是自变量,函数
是自变量,函数![]() 。当自变量
。当自变量![]() 发现变化时候,令改变的大小是
发现变化时候,令改变的大小是![]() ,那么
,那么![]() ;上面的导数可以变换成
;上面的导数可以变换成
而![]() 其实是Y轴上的变化
其实是Y轴上的变化![]() ;所以上面的导数可以变化成
;所以上面的导数可以变化成
上面的导数公式中![]() 指的是在X轴上的变化,
指的是在X轴上的变化,![]() 指的是在Y轴上的变化,当
指的是在Y轴上的变化,当![]() 越来越靠近0那么变化将会越来越小,我们把这种“x中十分微小的变化”用另外一种表示:
越来越靠近0那么变化将会越来越小,我们把这种“x中十分微小的变化”用另外一种表示:![]() ,同样的道理Y轴微小变化用:
,同样的道理Y轴微小变化用:![]() ;
;
二阶导数和高阶导数
二阶导数就是导数的导数,记:![]() 或者
或者![]() ,三阶导数就是导数的导数的导数,记:
,三阶导数就是导数的导数的导数,记:![]() 或者
或者![]()
【例三】如果![]() ,那么
,那么![]() ,设
,设![]() ,求
,求![]() 的导数
的导数![]()
直接套公式
![]()
同理可以计算出三阶导数、四阶导数.....这里不做讲解