PCL最小二乘法进行平面拟合原理

1 最小二乘原理

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小 。在图像领域，最小二乘法常用于直线、曲线拟合、平面拟合等。
首先我们来熟悉下最小二乘问题。考虑线性方程组Ax=b，其中A为mxn矩阵且m>n。这个方程一般不存在解x。因此，我们的任务是求最小化范数||A$\bar{x}$-b||的向量$\bar{x}$。当x取遍所有值时，Ax将遍历A的整个列空间。因此我们的任务是在A的列空间中寻求最接近b的那个向量。因此，A$\bar{x}$-b必然是与A的列空间垂直的向量。因此
$A^T(A\bar{x}-b)=0$
于是我们得到一个nxm的线性方程
$(A^{T}A)\bar{x}=A^{T}b$
可以通过$\bar{x}=(A^{T}A{)}^{-1}{A}^{T}b$来求解
这个方程有多个叫法，有些称为正规方程，有些称为法线方程。这个解$\bar{x}$其实就是Ax=b的最小二乘解。
很多人可能觉得这个不够直观，那么可以从另外一个角度去解释，举个例子：
$\{\begin{array}{l}{x}_1+x_2=2\\ x_1-x_2=1\\ x_1+x_2=3\end{array}$
根据线性代数的知识，m个方程n个未知量m>n时通常无解，但是虽然不能求出Ax=b的解，那何不退而求其次，去寻找与解近似的向量$\bar{x}$。
那么如何定义与解相似，一般使用欧氏距离来进行度量，即两点间的距离，这其实很好理解，越相似，欧氏距离越近，这样求出的$\bar{x}$被称为最小二乘解。
将我们开始举的例子写成矩阵形式：
$\left[\begin{array}{cc}1& 1\\ 1& -1\\ 1& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}2\\ 1\\ 3\end{array}\right]$
写成等价方程为：
$x_1\left[\begin{array}{c}1\\ 1\\ 1\end{array}\right]+x_2\left[\begin{array}{c}1\\ -1\\ 1\end{array}\right]=\left[\begin{array}{c}2\\ 1\\ 3\end{array}\right]$
对于任意 mxn 方程组Ax=b都可以看做向量方程：
$x_1{v}_1+x_2{v}_2+...+x_n{v}_n=b$
其实也就是把b 看做A的列向量的线性组合，对应的系数即为 $x_i$ ，对于举的例子来说，就是把b表示为另外两个三维向量的线性组合，由于三维空间中两个三维向量的组合生成一个平面，方程仅当b在这个平面上才有解，推广至m个方程n个未知量m>n 时也是相同的情况。如下图所示，向量A$\bar{x}$-b(右下图虚线部分)与A所在平面垂直，也就是该平面的法向量。

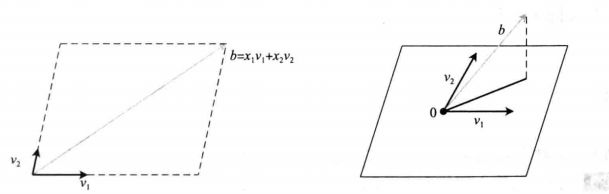
以上就是对最小二乘的直观上的解释。当然，想把最小二乘法学透彻光看这些还是不够。因为还存在非线性，带约束和不带约束等情况。

2 最小二乘拟合平面

下面来介绍下最小二乘拟合平面的原理，已知空间中的一些离散点，对其进行平面拟合。首先，平面方程的一般式如下：
$$ax+by+cz+d=0$$
我们假设$c\ne 0$的情况。那么 $$z=-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}$$
令$a_0=-\frac{a}{c}$, $a_1=-\frac{b}{c}$ , $a_2=-\frac{d}{c}$
于是$$z=a_{0}x+a_{1}y+a_2$$
如果该平面内存在一系列的点集$\{(x,y,z)|(x,y,z)\in (x_i,y_i,z_i),i=0,1,2,...,n-1\}$
按照最小二乘原则，使得误差平方和最小。
$$\sum _{i=0}^{n-1}(z-z_i{)}^2=min$$
也就是指$S={\sum }_{i=0}^{n-1}(a_{0}x+a_{1}y+a_2-z_i{)}^2$最小，其中$a_0,a_1,a_2$是未知数。
为了使得上式最小，要求$$\frac{\partial S}{\partial a_k}=0,k=0,1,2$$
即$$\{\begin{array}{l}{\sum }_{i=0}^{n-1}2(a_0{x}_i+a_1{y}_i+a_2-z_i)x_i=0对a_0求偏导\\ {\sum }_{i=0}^{n-1}2(a_0{x}_i+a_1{y}_i+a_2-z_i)y_i=0对a_1求偏导\\ {\sum }_{i=0}^{n-1}2(a_0{x}_i+a_1{y}_i+a_2-z_i)=0对a_2求偏导\end{array}$$
化简得$$\{\begin{array}{l}{a}_0{\sum }_{i=0}^{n-1}{x}_i^2+a_1{\sum }_{i=0}^{n-1}{x}_i{y}_i+a_2{\sum }_{i=0}^{n-1}{x}_i={\sum }_{i=0}^{n-1}{x}_i{z}_i\\ a_0{\sum }_{i=0}^{n-1}{x}_i{y}_i+a_1{\sum }_{i=0}^{n-1}{y}_i^2+a_2{\sum }_{i=0}^{n-1}{y}_i={\sum }_{i=0}^{n-1}{y}_i{z}_i\\ a_0{\sum }_{i=0}^{n-1}{x}_i+a_1{\sum }_{i=0}^{n-1}{y}_i+n{a}_2={\sum }_{i=0}^{n-1}{z}_i\end{array}$$
可以将上面的式子写成矩阵形式，方便计算
$$\left[\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i^2& {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{x}_i\\ {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{y}_i^2& {\sum }_{i=0}^{n-1}{y}_i\\ {\sum }_{i=0}^{n-1}{x}_i& {\sum }_{i=0}^{n-1}{y}_i& n\end{array}\right]\left[\begin{array}{c}{a}_0\\ a_1\\ a_2\end{array}\right]=\left[\begin{array}{c}{\sum }_{i=0}^{n-1}{x}_i{z}_i\\ {\sum }_{i=0}^{n-1}{y}_i{z}_i\\ {\sum }_{i=0}^{n-1}{z}_i\end{array}\right]$$
现在，我们马上可以得到我们想要的平面方程系数了,解这个方程有多种方法。大部分人对于SVD分解求解的方式比较熟悉，那下面介绍一种不怎么常用的方法，就是使用克拉默法则。那这个法则是什么意思呢？可以参考 链接.
总的来说,如果求解$Ax=b$就是用b分别去替换等式坐标矩阵$A$的每一列，求出替换后的$A^{{}^{\prime }}$行列式，然后除以替换前的$A$的行列式。分别求出$a_i，i=0,1,2$.
所以，所得的方程系数为
$$a_0=\frac{\left|\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i{z}_i& {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{x}_i\\ {\sum }_{i=0}^{n-1}{y}_i{z}_i& {\sum }_{i=0}^{n-1}{y}_i^2& {\sum }_{i=0}^{n-1}{y}_i\\ {\sum }_{i=0}^{n-1}{z}_i& {\sum }_{i=0}^{n-1}{y}_i& n\end{array}\right|}{\left|\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i^2& {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{x}_i\\ {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{y}_i^2& {\sum }_{i=0}^{n-1}{y}_i\\ {\sum }_{i=0}^{n-1}{x}_i& {\sum }_{i=0}^{n-1}{y}_i& n\end{array}\right|}{a}_1=\frac{\left|\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i^2& {\sum }_{i=0}^{n-1}{x}_i{z}_i& {\sum }_{i=0}^{n-1}{x}_i\\ {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{y}_i{z}_i& {\sum }_{i=0}^{n-1}{y}_i\\ {\sum }_{i=0}^{n-1}{x}_i& {\sum }_{i=0}^{n-1}{z}_i& n\end{array}\right|}{\left|\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i^2& {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{x}_i\\ {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{y}_i^2& {\sum }_{i=0}^{n-1}{y}_i\\ {\sum }_{i=0}^{n-1}{x}_i& {\sum }_{i=0}^{n-1}{y}_i& n\end{array}\right|}{a}_2=\frac{\left|\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i^2& {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{x}_i{z}_i\\ {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{y}_i^2& {\sum }_{i=0}^{n-1}{y}_i{z}_i\\ {\sum }_{i=0}^{n-1}{x}_i& {\sum }_{i=0}^{n-1}{y}_i& {\sum }_{i=0}^{n-1}{z}_i\end{array}\right|}{\left|\begin{array}{ccc}{\sum }_{i=0}^{n-1}{x}_i^2& {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{x}_i\\ {\sum }_{i=0}^{n-1}{x}_i{y}_i& {\sum }_{i=0}^{n-1}{y}_i^2& {\sum }_{i=0}^{n-1}{y}_i\\ {\sum }_{i=0}^{n-1}{x}_i& {\sum }_{i=0}^{n-1}{y}_i& n\end{array}\right|}$$
到此，平面方程系数就完成了，如果有错误的地方烦请指正。
参考链接.