相机坐标系,世界坐标系,像素坐标系三者转换,以及OPENGLDEFocal Length和Opengl 的 Fov转换
目的:理解相机的工作原理,渲染和相机拍摄的深度图
最近研究相机参数和opengl渲染图像的参数关系。在遇到从相机坐标系到像素坐标系的过程中会遇到project 矩阵。
理论相机转化
基于相机的学习理论知识。正常我们使用相机参数构建project一般需要经过下面两个过程:
相机坐标系->图像坐标系->像素坐标系
假设我们获取了相机坐标系下的一个顶点 p ( x c , y c , z c ) p(x_c,y_c,z_c) p(xc,yc,zc),转化为图像上的顶点 p ( x i , y i ) p(x_i,y_i) p(xi,yi)。它的转为矩阵为 M p r o j M_{proj} Mproj
下面我们将介绍几个步骤:
- 相机坐标系到图像坐标系 M p 2 c M_{p2c} Mp2c
相同的位置,不同的相机会得到不同的图片。由此可见这个过程一般跟相机的参数有关。相机的一些参数一般在相机的说明书中,也可以在网上找到对应款式的说明文档,有的甚至配置文件里面(比如扫描仪中的图像相机相机参数都有)。为了理解这些参数的功能,我们需要了解一下相机成像的原理(小孔成像)。

图像中的坐标系为 ( O ′ x , O ′ y ) (O'x, O'y) (O′x,O′y), 相机坐标系为 ( O c x c , O c y c , O c z c ) (O_cx_c, O_cy_c , O_cz_c) (Ocxc,Ocyc,Oczc) , 方便理解 ,转换一下可视图。因为 ( O ′ x , O ′ y ) (O'x, O'y) (O′x,O′y) 和 ( O c x c , O c y c , O c z c ) (O_cx_c, O_cy_c , O_cz_c) (Ocxc,Ocyc,Oczc) 在 ( O c x c , O c y c ) (O_cx_c, O_cy_c) (Ocxc,Ocyc) 平行。因此根据几何的对称性,将图像坐标系移动到镜像的位置,如下图。其中 ∠ O c A B \angle{O_cAB} ∠OcAB为直角。图片画的不是特别准确。
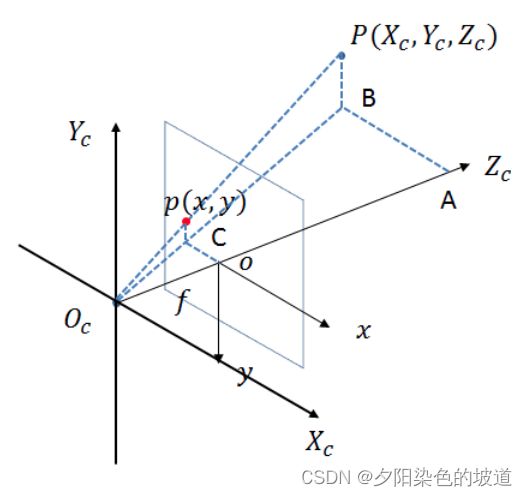
因为相似三角形(1):
△ A B O c ∼ △ o C O c \bigtriangleup ABO_c \sim \bigtriangleup oCO_c △ABOc∼△oCOc
得到下面公式:
O c o O c Z c = o C A B = O c C O c B ( 1 ) \frac{O_co}{O_cZ_c} = \frac{oC}{AB} = \frac{O_cC}{O_cB} \space \space \space (1) OcZcOco=ABoC=OcBOcC (1)
另一表达方式(因为 O c O_c Oc 为原点,换了符号)为下面:
O c o O c Z c = f Z c ( 2 ) \frac{O_co}{O_cZ_c} = \frac{f}{Z_c} \space \space \space (2) OcZcOco=Zcf (2)
o C A B = x X c ( 3 ) \frac{oC}{AB} = \frac{x}{X_c} \space \space \space (3) ABoC=Xcx (3)
因为相似三角形(2):
△ A B O c ∼ △ o C O c \bigtriangleup ABO_c \sim \bigtriangleup oCO_c △ABOc∼△oCOc
得到下面公式:
O c C O c B = C p B P ( 4 ) \frac{O_cC}{O_cB} = \frac{Cp}{BP} \space \space \space (4) OcBOcC=BPCp (4)
另一表达方式(因为 O c O_c Oc 为原点,换了符号)为下面:
C p B P = y Y c ( 5 ) \frac{Cp}{BP} = \frac{y}{Y_c} \space \space \space(5) BPCp=Ycy (5)
因为 ( 1 ) ( 2 ) ( 3 ) ( 4 ) ( 5 ) (1)(2)(3)(4)(5) (1)(2)(3)(4)(5)公式得到:
f Z c = x X c = y Y c \frac{f}{Z_c} = \frac{x}{X_c} = \frac{y}{Y_c} Zcf=Xcx=Ycy
进一步转化为公式如下:
x = f ∗ X c Z c ( 6 ) x=\frac{f*X_c}{Z_c} \space \space \space(6) x=Zcf∗Xc (6)
y = f ∗ Y c Z c ( 7 ) y=\frac{f*Y_c}{Z_c} \space \space \space(7) y=Zcf∗Yc (7)
把其中 ( 6 ) , ( 7 ) (6),(7) (6),(7)公式写成矩阵的形式得到如下:
[ x y z ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] \begin{bmatrix} x\\ y \\ z \end{bmatrix} = \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} X_c\\ Y_c \\ Z_c \\ 1 \end{bmatrix} ⎣⎡xyz⎦⎤=⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
最后得到的矩阵方程 M p 2 c M_{p2c} Mp2c为下面:
M p 2 c = [ f 0 0 0 0 f 0 0 0 0 1 0 ] M_{p2c}= \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} Mp2c=⎣⎡f000f0001000⎦⎤
简写公式可以得到:
[ x y z ] = M p 2 c [ X c Y c Z c 1 ] \begin{bmatrix} x\\ y \\ z \end{bmatrix} = M_{p2c}\begin{bmatrix} X_c\\ Y_c \\ Z_c \\ 1 \end{bmatrix} ⎣⎡xyz⎦⎤=Mp2c⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
这时候获取的 [ x y z ] \begin{bmatrix} x\\ y \\ z \end{bmatrix} ⎣⎡xyz⎦⎤为物理的为单位。不是像素为单位,因此需要转化为像素为单位,它需要每个像素的具体的物理长度。需要相机的sensor参数。下面将介绍相机坐标到像素坐标。
- 图像坐标系转为像素坐标系 M i 2 p M_{i2p} Mi2p
需要将相机坐标系转化为像素坐标系,它涉及到两个问题,
1)两个坐标系问题。在图像坐标系上,一般原点在中心点。而我们传统的像素显示坐标系原点为图像的左上角,需要平移这个向量。
2)单位转化问题:需要对知道每个像素有多少物理单位(一般是mm),物理单位为毫米。对于两者转化,需要知道 d x , d y d_x,d_y dx,dy分别表示每一列和每一行表示多少mm,表示一列的宽度 1 p i x e l = d x m m 1 \space pixel = d_x \space mm 1 pixel=dx mm;一行的宽度 1 p i x e l = d y m m 1 \space pixel = d_y \space mm 1 pixel=dy mm,一般情况下 d x = d y d_x=d_y dx=dy。因此 x x x坐标表示的像素为 x d x \frac{x}{dx} dxx,相应的 y y y坐标表示的像素为 y d y \frac{y}{dy} dyy
图示两个坐标系如下:

通过平移坐标系转化得到如下公式:
u = x d x + u 0 ( 8 ) u= \frac{x}{d_x}+u_0 \space \space \space (8) u=dxx+u0 (8)
v = y d y + v 0 ( 9 ) v= \frac{y}{d_y}+v_0 \space \space \space (9) v=dyy+v0 (9)
把其中 ( 8 ) , ( 9 ) (8),(9) (8),(9)公式写成矩阵的形式得到如下:
[ u v 1 ] = [ 1 d x 0 u 0 1 d y 0 v 0 0 0 1 ] [ u v 1 ] \begin{bmatrix} u\\ v \\1 \end{bmatrix}= \begin{bmatrix} \frac{1}{d_x}&0&u_0 \\ \frac{1}{d_y}&0&v_0 \\0&0&1 \end{bmatrix}\begin{bmatrix} u\\ v \\1 \end{bmatrix} ⎣⎡uv1⎦⎤=⎣⎡dx1dy10000u0v01⎦⎤⎣⎡uv1⎦⎤
得到矩阵公式为:
M i 2 p = [ 1 d x 0 u 0 1 d y 0 v 0 0 0 1 ] M_{i2p}= \begin{bmatrix} \frac{1}{d_x}&0&u_0 \\ \frac{1}{d_y}&0&v_0 \\0&0&1 \end{bmatrix} Mi2p=⎣⎡dx1dy10000u0v01⎦⎤
总结上面两种转化得到:
M p r o j = [ 1 d x 0 u 0 1 d y 0 v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] M_{proj}= \begin{bmatrix} \frac{1}{d_x}&0&u_0 \\ \frac{1}{d_y}&0&v_0 \\0&0&1 \end{bmatrix} \begin{bmatrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} Mproj=⎣⎡dx1dy10000u0v01⎦⎤⎣⎡f000f0001000⎦⎤
最后得到公式投影矩阵为:
M p r o j = [ f d x 0 u 0 0 0 f d y v 0 0 0 0 1 0 ] = [ f x 0 u 0 0 0 f x v 0 0 0 0 1 0 ] M_{proj}= \begin{bmatrix} \frac{f}{d_x}& 0 & u_0 & 0 \\ 0 & \frac{f}{d_y} & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} = \begin{bmatrix} f_x & 0 & u_0 & 0 \\ 0 & f_x & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} Mproj=⎣⎢⎡dxf000dyf0u0v01000⎦⎥⎤=⎣⎡fx000fx0u0v01000⎦⎤
通过公式理解关系,得到 f x = f d x f_x=\frac{f}{d_x} fx=dxf,它表示focal length有多少像素(这是像素单位),同理 f y = f d y f_y=\frac{f}{d_y} fy=dyf也表示有多少像素,一般情况下 d x = d y d_x=d_y dx=dy,且focal length为一个,上图中的 f f f。
总结得到如下:
M p r o j = [ f x 0 u 0 0 0 f x v 0 0 0 0 1 0 ] M_{proj}= \begin{bmatrix} f_x & 0 & u_0 & 0 \\ 0 & f_x & v_0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} Mproj=⎣⎡fx000fx0u0v01000⎦⎤
Opengl坐标渲染理论
基于相机的OPENGL理论知识。正常我们使用相机参数构建project需要fov,aspect ratio,near,far比较多。其中我们发现有4个参数在具体的渲染中,能够准确渲染空间需要的参数,且它们易于理解,且切开一个空间,用于归一化操作,易于渲染的计算。详细的请百度learnopengl关于相机的设置。它设置了关于上面的4个参数。它的project有两种,下面我将介绍它们的原理:
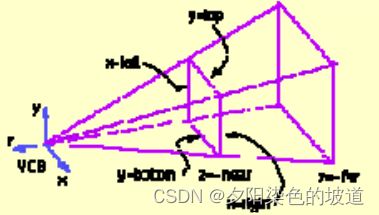
如果不转化为fov,aspect ratio,near,far,可以直接project矩阵,通过glFrustum完成。但是在学习opengl渲染中,通常使用的gluPerspective,它使用的参数为fov,aspect ratio,near,far。我们可以直接在shader里面设置project 矩阵来获取渲染的project矩阵。它也是模仿gluPerspective生成project矩阵, 同时,也可以通过转化为上述的4个,由opengl的gluPerspective帮你生成project矩阵。这两种方法都可以。
1)相机的参数转化为fov,aspect ratio,near,far这四个参数。
先理解这四个参数:
1)Field of view (FOV), aspect ratio
Aspect ratio is the x/y ratio of the final displayed image
FOV:表示张开的视野的角度,见下图。
2)near,far 表示远近的切平面距离原点的距离,见图的两个平行平面。
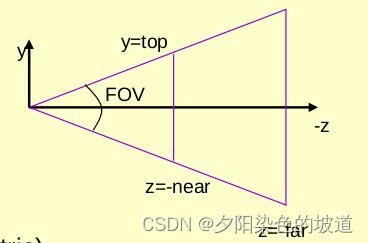
上图的关系可以看到:

如果需要渲染跟图像一致的图片话图片表示为img,我们通过图像设置的aspect ratio和FOV
根据定义,ratio is the x/y ratio of the final displayed image,
计算得到公式如下:
a s p e c t = i m g . c o l s i m g . r o w s aspect=\frac{img.cols}{img.rows} aspect=img.rowsimg.cols
带入上述的公式,top对应于半个y轴,也就是在像素坐标系下的pixelwidth,为
t o p = p i x e l w i d t h 2.0 top = \frac{pixelwidth}{2.0} top=2.0pixelwidth
其中near对应于focal length(像素坐标系)它在像素坐标系下的。单位统一。
后面转化为公式如下:
F O V = 2.0 ∗ a t a n f ( p i x e l w i d t h 2.0 ∗ f o c a l L e n g t h ) ∗ π 180.0 FOV=2.0*atanf({\frac{pixelwidth}{2.0*focalLength}})*\frac{\pi}{180.0} FOV=2.0∗atanf(2.0∗focalLengthpixelwidth)∗180.0π
对于near 和far 设置的距离可以尽量近和远。
它的矩阵为如下:

设置后,渲染的就和相机拍摄的图像一致了。
后续加入推导过程。