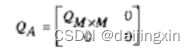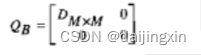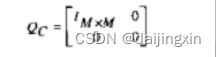OFDM学习笔记（四）（信道估计简介）
目录
- 1.基本介绍
- 2.慢衰落信道下的信道估计算法
-
- 2.1 基于DFT的信道估计算法
- 2.2 基于SVD的信道估计算法
- 2.3 基于滤波器的信道估计算法
- 2.4 最大似然估计算法
相干解调在实际中应用的比差分解调多很多。而信道估计作为相干解调的主要技术就尤为重要。
信道估计器是接收机一个很重要的组成部分。在OFDM系统中，信道估计器的设计上要有两个问题:** 一是导频信息的选择，由于无线信道的时变特性，需要接收机不断对信道进行跟踪，因此导频信息也必须不断的传送: 二是既有较低的复杂度又有良好的导频跟踪能力的信道估计器的设计，在确定导频发送方式和信道估计准则条件下，寻找最佳的信道估计器结构。 **在实际设计中，导频信息的选择和最佳估计器的设计通常又是相互关联的，因为估计器的性能与导频信息的传输方式有关。
1.基本介绍
信道估计可以作为信道对输入信号影响的一种数学表示，好的信道估计就是使估计误差最小的算法。
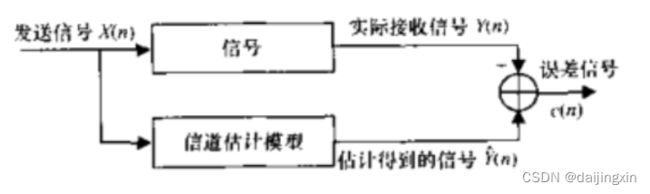
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 图1 信道估计过程示意图
通过信道佔计算法，接收机可以得到信道的冲激响应，在现代无线通信系统中，信道的信息已经得到了充分的利用。自适应的信道均衡器利用信道估计来对抗ISI的影响。分集技术利用信道佔计，实现与接收信号最佳匹配的接收机。最大似然检测通过信道估计使得接收端错误概率最小化。此外，信道估计的个重要的好处在于它使得相干解调成为可能。因为相干解调需要知道信号的相位信息，与非相干解调相比，可以提高系统的整体性能，而信道估计技术使之成为可能。
总的来说信道估计算法有两种，一种是基于训练序列的估计算法，一种是盲估计算法。
基于训练序列的信道估计算法是指利用接收机已知的信息来进行信道估计。它的一个好处在于其应用广泛，几乎可以用于所有的无线通信系统。它的缺点也是显而易见的，训练序列占用了信息比特，降低了信道传输的有效性，浪费了带宽。另外，在接收端，要将整帧的信号接收后才能提取出训练序列进行信道估计，带来了不叫避免的时延，所以对帧结构提出了限制要求，比如快哀信道下，由于信道的相关时间可能小于帧长，基于训练序列的信道估计算法应用受到限制。
盲估计不需要训练序列。盲估计算法的实现需要利用传输数据的内在的数学信息。这种算法与基于训练序列的算法相比虽然节约了带宽，但仍有自身的缺点。算法的运算量太大，灵活性很差，在实时系统中的应用受到了限制。但是盲估计算法不需要训练序列，与基于训练序列的信道估计算法相比提高了系统的效率，所以它在无线通信中的应用越来越受到重视。
通常通信系统中采用基于训练序列的信道估计算法。针对不同的信道情况，我们将基于训练序列的信道估计分为基于慢衰信道下的信道估计和基于快衰信道下的信道估计，分别对应块状导频和梳状导频。需要说明的是，这里的慢衰和快衰信道与道常意义下的馒哀和快衰信道不同，这里所说的快衰和慢收足根据信道与信号变化快慢的相对关系而确定的。我们定义如果信道在OFDM信号一帧的时间内保持准静止，则称之为慢衰信道:如果在一帧时间内发生显著变化，则称之为快衰信道。
2.慢衰落信道下的信道估计算法
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 图2 慢衰落信道下的信道估计示意图
首先是最小平方信道估计算法，LS算法受高斯白噪声和子载波间干扰(ICI)的影响很大,所以这种估计算法的准确度受到限制。
而基于最小均方误差(MMSE，Minimum Mean Square Error)信道估计算法，对于子ICI和高斯白噪有很好的抑制作用，所以MMSE算法的效果要好于LS算法，在相同的MSE下，MMSE算法在SNR上:要优于LS算法10dB~ 15dB左右。但是MMSE算法的最大缺点在于算法的复杂度太高，随着抽样点成指数增长。
为了减小算法的复杂度，一种低阶的基于频域相关的算法受到了人们的重视，称为低阶LMMSE(Low Rank Linear MMSE)。它的核心思想在于利用命异值分解得到最优的低阶估计器，同时它的性能与MMSE近似。
基于训练序列的信道估计方法的基本思想就足利用发端和收端都知的序列进行信道估计。
基于训练序列的信道估计方法大致可以分为两类:一类是在频域内进行信道估计，另一类是在时域内进行估计。根据OFDM的基本构成，可以在时域和频域内进行导频的插入。导频插入的形式有很多种，我们将对两种典型的插入法进行研究，即块状导频和梳状导频，它们分别对应慢衰和快衰的信道情况。
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 图3 块状导频下的OFDM符号结构示意图
块状导频周期性地在时域内插入特定的OFDM符号,在信道中传输。这种导频的插入方式适用于慢衰的无线信道中，即在个OFDM块中，信道视为准静止。因为这种训练序列包括所有的子载波，不需要在接收端进行频域内的插值，所以这种导频的设计方案对频率选择性不是很敏感。这种信道估计算法一般展于LS和MMSE。
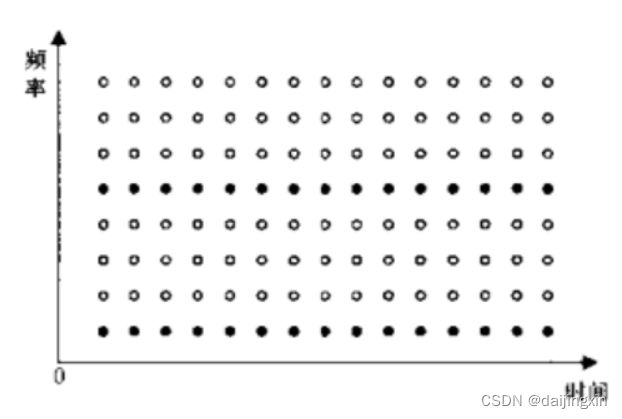
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 图4 梳状导频下的OFDM符号结构示意图
梳状导频均匀分们于每个OFDM块中。假设两种导频的导频载荷相同，梳状导频有更高的重传率，因此梳状导频在快衰信道下估计的效果则好。但是在梳状导频的情况下，非导频子载波上的信道特性只有根据对导频子载波上，的信道特性的插值才能得到，所以这种导频万式对频率选择性衰落比较敏感。为了有效对抗频率选择性衰落，子载波间隔要求比信道的相关带宽要小很多。
2.1 基于DFT的信道估计算法
OFDM的符号结构使得系统的信道估计可以在时域和频域内同时进行，这种信道估计算法基于把号频插入到二维的时频格图中。但是这种算法过于复杂，在实际应用中受到了限制。为了降低二维信道估计的复杂度，可以分别在时域和频域内进行信道估计，即进行两个一维的信道佔计，于是人们提出种先在时域内进行信道估计，再进行频域估计的信道估计算法。**这种算法利用了两个相互独立的有限冲激响应维纳滤波器，两个滤波器分别应用在时域和频域内。**进一步简化，信道估计可以只在时域或只在频域内进行，这种算法因为简便易行，应用范围很广。
基于DFT的信道估计算法因为易于实现，性能很好，所以备受关注。基于DFT的信道估计算法首先进行LS算法的信道估计，再经过IDFT进入时域，在时域内进行线性变换(具体的变换方法各有不同，将在后面的篇幅中进行讨论)，最后经过DFT进入频域。这种算法利用时域内信道能量集中在相对较少的抽样点上，提出了3种简化的算法，它们分别为:将能量较低的抽样点视为零、忽略抽样点的互相关以及忽略抽样点方差的差异。
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 表1 基于DFT信道估计算法的对比
| 估计器 | 简化 | 线性变换Q | 矩阵大小 | 运算量 |
|---|---|---|---|---|
| LMMSE | 无 | 无 | N ∗ N N*N N∗N | N + 1 N+1 N+1 |
| A | M M M个参数 |  |
M ∗ M M*M M∗M | l o g 2 N + M 2 N + 1 log_2N+\frac{M^2}{N}+1 log2N+NM2+1 |
| B | 对角矩阵 |  |
M ∗ M M*M M∗M | l o g 2 N + M N + 1 log_2N+\frac{M}{N}+1 log2N+NM+1 |
| C | 单位阵 |  |
M ∗ M M*M M∗M | l o g 2 N + 1 log_2N+1 log2N+1 |
| LS | 无 | 无 | 无 | 1 |
\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad 表2 各种估计算法的平均误符合率
| 估计器 | MSE |
|---|---|
| LMMSE |  |
| A |  |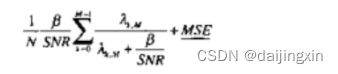
| B |  |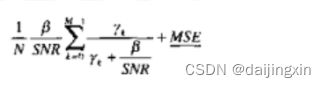
| C |  |
| LS |  |
2.2 基于SVD的信道估计算法
LMMSE估计算法只利用频域内的相关性，所以比普通的基于时频二维的算法的复杂度要低，但算法复杂度仍然很高，在实际应用中受到限制:基于DFT的算法在信道同步定时不是很理想的时候，会出现采样不匹配的缺陷。为了进一步提商信道估计的性能，一种方法是利用最佳低阶理论简化LMMSE算法，另外一种低阶近似算法是基于DFT, 简化LMMSE算法。简化算法是通过奇异值分解(SVD, Singular Value Decomposition)来实现的。
2.3 基于滤波器的信道估计算法
(1) Hoeher提出的频域维纳(Wiener)滤波器，由有限长度单位冲激响应滤波器(FIR)组成，缺点是硬件的复杂度很高，前而已经介绍过。
(2)固定抽头滤波器(Fixed tap filter)， 利用频域内固定抽头的滤波器，可以通过平均子载波信号矢量消除噪声，从而提高信道估计的精确度，这种滤波器起到一种均衡的效果。而且，这种FIR滤波器应用移位来代替相乘器，从而降低了设备的复杂度。
(3)可调节滤波器(Adaptive filter) 为了跟踪信道并及时反映信道的变化，提高信道估计的性能，采用可调节滤波器，即滤波器的抽头参数是变化的，这种变化是根据每个子载波幅度和相邻子载波矢量的差异来进行的。
2.4 最大似然估计算法
最大似然算法(ML，Maxirmum Likelihood)是佔计和检测算法中的一种基础方法，虽然由于它的复杂度很大使其应用受到限制，但这并不妨碍它在检测与估值中的应用，尤其是在理论分析时。
首先，简单介绍一下最大似然算法和最大后验概率(MAP，Maximum A PosteriorProbability)估值算法。设发端信号为x(1)，收端信号为y(t)，为了使接收端错误最小，就要求后验概率P(x(t)|y(t))最大。由贝叶斯公式:
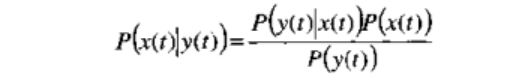
经过推导可以得到MAP与ML之间的关系，即满足ML准则一定满足MAP准则，但满足MAP准则不一定满足ML准则。
因此以ML准则为基础，进行OFDM的信道估计算法研究。该算法采用迭代方法，首先利用导频或前一个OFDM符号计算得到信道的初始状态，再用直接判决(Decision Directed)模式进行迭代运算跟踪信道的变化。OFDM系统的结构特点为这种算法提供了方便。
ML算法从包含导频的OFDM符号开始，初始信道的ML估计仅仅从导频符号得到，在此基础之上，可以得到发送信号的第一次估计值， 然后将导频符号和估计得到的发送符号进行反馈，迭代得刭更精确的信道特性，直到估计精确到预先设定的标准。