概率dp专辑
求概率
uva11021 http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1962
给定n,k,m
有k个麻雀,每只活一天就会死,临死之前生出i只麻雀的概率为pi , 0<= i <n
问m天后,麻雀死光的概率
独立事件同时发生是每个事件的概率相乘, 每只麻雀都是独立的,只要求出一只麻雀m天后死亡的概率dp[m], 那么k只麻雀m天后死亡的概率为dp[m]^k
dp[i]表示i天后麻雀全部死亡的概率, 这个全部死亡即自己死亡,后代也死亡
dp[i]可以分解为n个子事件,生0->n-1个孩子,如果生j个孩子,那么j个孩子要在i-1天后死亡,这样全部的麻雀才会在i天后死亡,j个孩子要在i-1天后死亡是独立事件同时发生
所以是dp[i-1]^j,生j个孩子的概率为pj, 所以生j个孩子且i-1天后死亡也是独立事件,概率为pj * dp[i-1]^j
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 f[i] = p0 19 */ 20 const int N = 1000 + 10; 21 double p[N],dp[N]; 22 int main() 23 { 24 int n, k, m, t, tCase = 1; 25 scanf("%d", &t); 26 while (tCase <= t) 27 { 28 scanf("%d%d%d", &n, &k, &m); 29 for (int i = 0; i < n; ++i) 30 scanf("%lf", &p[i]); 31 dp[0] = 0;//0天后死亡是不可能的,所以概率是0 32 dp[1] = p[0];//一天后死亡的概率是不生孩子的概率 33 for (int i = 2; i <= m; ++i) 34 { 35 dp[i] = 0; 36 for (int j = 0; j < n; ++j) 37 dp[i] += p[j] * pow(dp[i - 1], j); 38 } 39 printf("Case #%d: %.7lf\n", tCase++, pow(dp[m], k)); 40 } 41 return 0; 42 }
http://acm.hit.edu.cn/hoj/problem/view?id=2866
给定n,m 表示第一个人的血量和第二个人的血量
然后接下来两行,每行6个数字,分别表示摇骰子得到点数1->6的概率
要我们求第一个人赢的概率
p1,p2,p 表示进行一次游戏,第一个人赢,第二个人赢,平局的概率
q1,q2表示前n局中,第一个人赢一局,其他都是平局, 第二个人赢一局,其他都是平局的概率,如图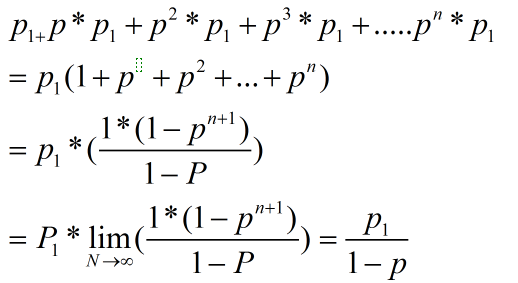
q1 = p1/(1-p)
q2 = p2/(1-p)
dp[i][j] 表示第一个人赢i次,第二个人赢j次, dp[i][j] = dp[i-1][j]*q1 + dp[i][j-1]*q2
为什么是dp[i][j] = dp[i-1][j]*q1 + dp[i][j-1]*q2;
而不是 dp[i][j] = dp[i-1][j]*p1 + dp[i][j-1]*p2;
因为进行一局游戏,有第一个人赢,第二个人赢,平局
不可能理想到只进行了一次游戏,就可能第一个人赢 即dp[i-1][j]*p1,
所以要一个人赢一局,可能经过了n局,然后才赢一局, q1,q2就是经过了很多平局,才赢得一局的情况
答案是dp[hp2][0->hp1-1]
初始化条件是dp[0][0] = 1,这是必然的,因为刚开始的,必定两个人都没有赢过一次,所以是1,必定发生
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 double dp[2001][2001]; 21 int main() 22 { 23 int hp1, hp2; 24 double a[6], b[6]; 25 int i, j; 26 double p1, p2, p, q1, q2; 27 while (scanf("%d%d", &hp1, &hp2) != EOF) 28 { 29 p1 = p2 = p = q1 = q2 = 0; 30 for (i = 0; i < 6; ++i) 31 scanf("%lf", &a[i]); 32 for (i = 0; i < 6; ++i) 33 scanf("%lf", &b[i]); 34 for (i = 0; i < 6; ++i) 35 for (j = 0; j < i; ++j) 36 { 37 p1 += a[i] * b[j]; 38 p2 += a[j] * b[i]; 39 } 40 p = 1.0 - p1 - p2; 41 p == 1 ? q1 = q2 = 0 : q1 = p1 / (1 - p), q2 = p2 / (1 - p); 42 //q1 = p1 / (1.0 - p); 43 //q2 = p2 / (1.0 - p); 44 memset(dp, 0, sizeof(dp)); 45 dp[0][0] = 1.0; 46 for (i = 0; i <= hp2; ++i) 47 { 48 for (j = 0; j <= hp1; ++j) 49 { 50 if (j<hp1 && i) dp[i][j] += dp[i - 1][j] * q1; 51 if (i<hp2 && j) dp[i][j] += dp[i][j - 1] * q2; 52 } 53 } 54 double ans = 0; 55 for (j = 0; j < hp1; ++j) 56 ans += dp[hp2][j]; 57 printf("%.6lf\n", ans); 58 } 59 return 0; 60 }
poj 2151 http://poj.org/problem?id=2151
m t n
m到题目, t个队伍, n 冠军队最少解决n道题
t行,每行m个数字
表示每个队伍解决第i道题目的概率
问我们每个队伍至少解决一题,且冠军队至少解决n题的概率
p1为每个队伍至少解决一题的概率
p2为每个队伍解决k题的概率 1<=k<n
最终答案为p1-p2,每个队伍至少做出一题,且冠军队至少解决n题的概率
单独算出队伍至少解决k题的概率,每只队伍的概率相乘(独立事件同时发生)
dp[i][j][k] 为第i只队伍前j道题目解出k题的概率 dp[i][j][k] = dp[i][j-1][k-1] * p[i][j] + dp[j-1][k] *(1-p[i][j])
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 double p[1000+10][30+10]; 21 double dp[30 + 10][30 + 10]; 22 double s[33]; 23 int main() 24 { 25 int n, m, t, i, j, k; 26 while (scanf("%d%d%d", &m, &t, &n), m+n+t) 27 { 28 double p1, p2, tmp; 29 p1 = p2 = 1; 30 for (i = 1; i <= t; ++i) 31 { 32 tmp = 1; 33 for (j = 1; j <= m; ++j) 34 { 35 scanf("%lf", &p[i][j]); 36 tmp = tmp * (1 - p[i][j]);//tmp为一题都没做出来的概率 37 } 38 p1 = p1*(1 - tmp);//p1为每个队伍至少做出一题的概率 39 } 40 for (i = 1; i <= t; i++) 41 { 42 //dp[0][0] = 1; 43 memset(dp, 0, sizeof(dp)); 44 dp[0][0] = 1; 45 //for (j = 1; j <= m; ++j) 46 // dp[j][0] = dp[j - 1][0] * (1 - p[i][j]); 47 for (j = 1; j <= m; ++j) 48 { 49 dp[j][0] = dp[j - 1][0] * (1 - p[i][j]); 50 for (k = 1; k <=j; ++k) 51 { 52 dp[j][k] += dp[j - 1][k] * (1 - p[i][j]); 53 //if (k!=0) 54 dp[j][k] += dp[j - 1][k - 1] * p[i][j]; 55 } 56 } 57 tmp = 0; 58 for (k = 1; k < n; ++k) 59 tmp += dp[m][k]; 60 p2 = p2 * tmp; 61 } 62 printf("%.3f\n", p1 - p2); 63 } 64 return 0; 65 }
poj3071 http://poj.org/problem?id=3071
给定一个n, 表示有2^n个队伍进行比赛
给定一个2^n * 2^n的矩形
pij 表示第i队伍打败第j只队伍的概率
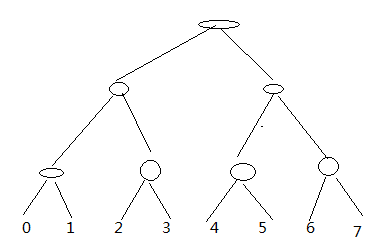
比赛的规则是第一只队伍和第二只打,第三只队伍和第四只打,赢的晋级,然后还是依照这样的规则,如图
要我们求哪只队伍最终获胜的概率最大,输出该队伍
dp[i][j] 表示第i次比赛,队伍j获胜, 设k为要与j比赛的队伍 dp[i][j] += sum(dp[i-1][j] * dp[j-1][k] * p[j][k] )
那么怎么判断所要与j比赛的,我们对队伍进行分组, 队伍号/(i<<(i-1)) 就是组号了, 如果是组号是偶数,那么要与后一只队伍比赛,如果是奇数,那么要与前一只队伍比赛
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 double dp[8][256], p[256][256]; 21 int main() 22 { 23 int n, i, j, k; 24 while (scanf("%d", &n), n != -1) 25 { 26 int m = 1 << n; 27 for (i = 0; i < m; ++i) 28 for (j = 0; j < m; ++j) 29 scanf("%lf", &p[i][j]); 30 for (i = 0; i < m; ++i) 31 dp[0][i] = 1;//dp[i][j]表示第i次比赛,获胜者是j的概率 32 for (i = 1; i <= n; ++i)//2^n个队伍每次淘汰一半的队伍,所以要进行n次比赛才能决出胜负 33 { 34 int t = 1 << (i-1); 35 for (j = 0; j < m; ++j) 36 { 37 dp[i][j] = 0; 38 int teamNumWin = j / t;//分组 39 for (k = 0; k < m; ++k) 40 { 41 int teamNumLose = k / t;//分组 42 if (teamNumWin % 2 == 0 && teamNumWin + 1 == teamNumLose)//如果组数是偶数,那么与后一组比赛 43 dp[i][j] += dp[i - 1][j] * dp[i - 1][k] * p[j][k]; 44 if (teamNumWin % 2 == 1 && teamNumWin - 1 == teamNumLose)//如果组数是奇数,与前一组比赛 45 dp[i][j] += dp[i - 1][j] * dp[i - 1][k] * p[j][k]; 46 } 47 } 48 49 } 50 double Max = 0; 51 int ans; 52 for (i = 0; i < m; ++i) 53 if (dp[n][i]>Max) 54 { 55 Max = dp[n][i]; 56 ans = i; 57 } 58 printf("%d\n", ans + 1); 59 } 60 return 0; 61 }
http://codeforces.com/problemset/problem/148/D
给定w,b 分别为袋子里白老鼠和黑老鼠的数量
先取到白老鼠的人赢,一轮游戏后,即两个人各取了一只后,会从带子里随机逃出一只老鼠,老鼠逃出的概率是均等的。
问第一个人赢的概率
dp[i][j] 表示有i只白鼠,j只黑鼠的时候,第一个人赢的概率
这个人可能这一轮就赢,即取到白老鼠dp[i][j] += i/(i+j);
也可能下一轮才赢,那么这一轮可能的情况是:
第一个人取到黑,第二个人取到黑,逃掉一只黑的 dp[i][j] += j/(i+j)*(j-1)/(i+j-1)*(j-2)/(i+j-2)*dp[i][j-3];
第一个人取到黑,第二个人取到黑,逃掉一只白的 dp[i][j] += j/(i+j)*(j-1)/(i+j-1)*i/(i+j-2)*dp[i-1][j-2];
还有一种可能是
第一个人取到黑,第二个人取到白, 但这不是我们要考虑的,我们要考虑的是第一个人赢的概率
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 dp[i][j] 表示有i只白鼠,j只黑鼠的时候,princess赢的概率 19 dp[i][j] = i/(i+j) + j/(i+j) * (j-1)/(i+j-1) * (j-2)/(i+j-2) * dp[i][j-3] + j/(i+j) * (j-1)/(i+j-1)*i/(i+j-2)*dp[i-1][j-2] 20 */ 21 double dp[1000 + 10][1000 + 10]; 22 int main() 23 { 24 int w, b, i, j; 25 scanf("%d%d", &w, &b); 26 for (i = 1; i <= w; ++i) 27 dp[i][0] = 1;//如果只有白,没有黑,那么第一次抓就会赢 28 for (i = 1; i <= w; ++i) 29 { 30 for (j = 1; j <= b; ++j) 31 { 32 dp[i][j] += (double)i / (i + j); 33 if (j >= 3) 34 dp[i][j] += (double)j / (i + j) * (double)(j - 1) / (i + j - 1) * (double)(j - 2)/(i + j - 2)*dp[i][j - 3]; 35 if (j >= 2) 36 dp[i][j] += (double)j / (i + j) * (double)(j - 1) / (i + j - 1) * (double)i / (i + j - 2)*dp[i - 1][j - 2]; 37 } 38 39 } 40 printf("%.9lf\n", dp[w][b]); 41 return 0; 42 }
poj http://poj.org/problem?id=3744
给定n, p 表示有n个地雷,p表示人走一步的概率,1-p表示人跳两步的概率, 人的其实位置在1
接下来n个数字表示n个地雷的位置, (地雷的位置不是递增的,坑爹啊)
我们求人安全走出雷区的概率
状态转移方程很简单dp[1] = 1 , 如果i不是雷区, dp[i] = dp[i-1] * p + dp[i-2] * (1-p), 如果i是雷区, dp[i]=0
但是雷区的长度实在是太长了,而这又是一个递推关系,所以我们可以用矩阵来优化
1--a[1]
a[1] + 1--a[2]
...进行分段
首先用矩阵快速幂求的dp[a[1]] ,dp[a[1]-1]
从而求的dp[a[1]+1] ,dp[a[1]],然后进行第二段矩阵快速幂,依次类推。
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 class Matrix 21 { 22 public : 23 double mat[2][2]; 24 void makeZero() 25 { 26 for (int i = 0; i < 2; ++i) 27 for (int j = 0; j < 2; ++j) 28 mat[i][j] = 0; 29 } 30 void makeUnit() 31 { 32 for (int i = 0; i < 2; ++i) 33 for (int j = 0; j < 2; ++j) 34 mat[i][j] = (i == j); 35 } 36 }; 37 Matrix operator*(const Matrix &lhs, const Matrix &rhs) 38 { 39 Matrix ret; 40 ret.makeZero(); 41 for (int k = 0; k < 2; ++k) 42 for (int i = 0; i < 2; ++i) 43 { 44 if (lhs.mat[i][k] == 0) continue; 45 for (int j = 0; j < 2; ++j) 46 ret.mat[i][j] += lhs.mat[i][k] * rhs.mat[k][j]; 47 } 48 return ret; 49 } 50 Matrix operator^(Matrix a, int n) 51 { 52 Matrix ret; 53 ret.makeUnit(); 54 while (n) 55 { 56 if (n & 1) 57 ret = ret * a; 58 n >>= 1; 59 a = a * a; 60 } 61 return ret; 62 } 63 int a[10 + 10]; 64 int main() 65 { 66 int n, i, x; 67 double p; 68 int pre; 69 Matrix aa; 70 double f1, f2; 71 while (scanf("%d%lf", &n, &p) != EOF) 72 { 73 bool flag = false; 74 for (i = 1; i <= n; ++i) 75 { 76 scanf("%d", &a[i]); 77 if (a[i] - a[i - 1] == 1) 78 flag = true; 79 } 80 sort(a + 1, a + n + 1); 81 for (i = 1; i <= n; ++i) 82 if (a[i] - a[i - 1] == 1) 83 flag = true; 84 if (flag) 85 printf("%.7lf\n", 0); 86 else 87 { 88 pre = 1; 89 f1 = 0; 90 f2 = 1; 91 for (i = 1; i <= n; ++i) 92 { 93 aa.mat[0][0] = p; 94 aa.mat[0][1] = 1; 95 aa.mat[1][0] = 1 - p; 96 aa.mat[1][1] = 0; 97 aa = aa ^ (a[i] - pre); 98 pre = a[i]+1; 99 100 //double tmpf2 = f2 * aa.mat[0][0] + f1*aa.mat[1][0]; 101 //double tmpf1 = f2 * aa.mat[0][1] + f1*aa.mat[1][1]; 102 //f2 = tmpf2; 103 //f1 = tmpf1; 104 //f2 = f1 * (1 - p); 105 //f1 = 0; 106 //这是根据上面的注释的代码推出来的 107 f2 = f2 * aa.mat[0][1] * (1 - p); 108 } 109 printf("%.7f\n", f2); 110 } 111 } 112 return 0; 113 }
uva10759 http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1700
给定n个骰子和数字x,要我们求掷n个骰子,点数至少为x的概率
dp[i][j] 为前i个骰子,点数为j的概率 dp[i][j] += dp[i-1][j-k]/6 j-k>=0, 初始条件dp[0][0] = 1;
1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 typedef unsigned long long LL; 16 const int INF = 1<<30; 17 /* 18 19 */ 20 struct node//因为要输出分数,所以建立一个数据结构,存分子和分母 21 { 22 LL x, y;//x/y 23 }; 24 node dp[30][200]; 25 LL gcd(LL a, LL b) 26 { 27 if (b == 0) 28 return a; 29 return gcd(b, a%b); 30 } 31 int main() 32 { 33 int n, x; 34 while (scanf("%d%d", &n, &x), n || x) 35 { 36 memset(dp, 0, sizeof(dp)); 37 dp[0][0].x = dp[0][0].y = 1; 38 int m = n * 6; 39 for (int i = 1; i <= n; ++i) 40 { 41 for (int j = i; j <= m; ++j) 42 { 43 for (int k = 1; k <= 6; ++k) 44 if (j - k >= 0 && dp[i - 1][j - k].y != 0) 45 { 46 if (dp[i][j].y == 0) 47 { 48 dp[i][j] = dp[i - 1][j - k]; 49 dp[i][j].y *= 6; 50 continue; 51 } 52 LL y = dp[i - 1][j - k].y * 6; 53 LL g = gcd(dp[i][j].y, y); 54 LL tmp = dp[i][j].y / g * y; 55 dp[i][j].x = dp[i][j].x * (tmp / dp[i][j].y) + dp[i - 1][j - k].x*(tmp / y); 56 dp[i][j].y = tmp; 57 //dp[i][j] += dp[i - 1][j - k] / 6; 58 } 59 } 60 } 61 62 node ans = dp[n][x]; 63 for (int i = x + 1; i <= m; ++i) 64 { 65 if (dp[n][i].y == 0) continue; 66 if (ans.y == 0) 67 { 68 ans = dp[n][i]; 69 continue; 70 } 71 LL g = gcd(ans.y, dp[n][i].y); 72 LL tmp = ans.y / g * dp[n][i].y; 73 ans.x = ans.x *(tmp / ans.y) + dp[n][i].x*(tmp / dp[n][i].y); 74 ans.y = tmp; 75 } 76 LL g = gcd(ans.x, ans.y); 77 if (g != 0) 78 { 79 ans.x /= g; 80 ans.y /= g; 81 } 82 if (ans.y != 0) 83 { 84 if (ans.x%ans.y == 0) 85 printf("%llu\n", ans.x / ans.y); 86 else 87 printf("%llu/%llu\n", ans.x, ans.y); 88 } 89 else 90 printf("0\n"); 91 } 92 return 0; 93 }
下面的是求期望的