transformer学习记录+python实现
transformer学习记录+python实现
- 简介
-
- 输入模块
- 位置编码
- 掩码
- 注意力机制
-
- 自注意力机制
- 多头注意力机制
- 前馈全连接层
- 规范化层
- 子层连接结构
- 编码器层
- 编码器
- 解码器层
- 解码器
- 输出部分
- 结语
简介
本文对着为对transformer的学习博客,主要参考b站的该视频链接
视频中很多地方没有讲得很清楚也有些代码细节错误,不过带着把整体流程走了一遍还是很棒的,对于一些细节部分我也进行了自己的思考与查阅。
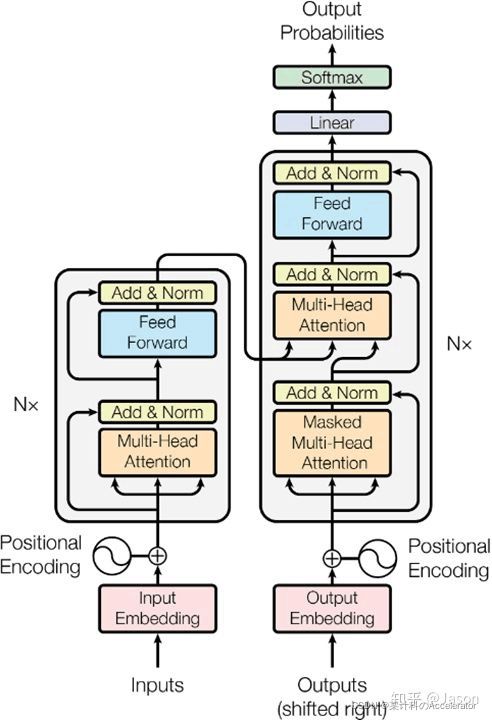
输入模块
import copy
import torch
import torch.nn as nn
import math
from torch.autograd import Variable
import torch.nn.functional as F
class Embeddings(nn.Module):
def __init__(self,d_model,vocab):
#d_model是词嵌入的维度,vacab是词表大小
super().__init__()
self.lut=nn.Embedding(vocab,d_model)
self.d_model=d_model
def forward(self,x):
return self.lut(x)*math.sqrt(self.d_model)
d_model=512#维度大小
vocab=1000#词表大小
x=Variable(torch.LongTensor([[100,2,421,999],[491,998,1,221]]))
#数字相当于词表中词语的下标,词表大小为1000,所以tensor数字范围为[0,999]
emb=Embeddings(d_model, vocab)
embr=emb(x)
#等效于emb.forward(x)
print(embr)
print(embr.shape)
输出结果:
tensor([[[-39.6184, -10.5092, 7.1710, ..., -19.9367, -10.8389, 17.1142],
[ 17.2396, -4.6296, -8.9631, ..., -9.4606, -27.8265, -8.0254],
[-12.7667, -19.6354, 20.9742, ..., -8.6860, 3.3338, -2.4481],
[ -1.6448, -9.4879, 48.4881, ..., -10.4297, 13.6739, 3.5179]],
[[-34.4081, -1.4890, 32.3946, ..., 1.9589, 5.8675, 7.0240],
[ 21.5126, 28.7549, 39.9685, ..., -29.9511, 6.3127, -64.7529],
[ -9.4844, -40.8318, 7.0417, ..., 22.7050, 32.7313, 4.8852],
[ -5.6594, -22.7754, 39.3119, ..., 12.8365, 1.6945, -25.7491]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
可以看出原先x中的每个数字被扩展成了 512 512 512维的向量,即从 2 ∗ 4 − > 2 ∗ 4 ∗ 512 2*4->2*4*512 2∗4−>2∗4∗512
位置编码
正弦编码的公式如下:
P E ( p o s , 2 i ) = sin ( p o s / 1000 0 2 i / d ) P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d}\right) PE(pos,2i)=sin(pos/100002i/d)
P E ( p o s , 2 i + 1 ) = cos ( p o s / 1000 0 2 i / d ) P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10000^{2 i / d}\right) PE(pos,2i+1)=cos(pos/100002i/d)
transformer中会将上述公式计算出的PE与原先的输入直接相加作为编码结果。
这里为什么可以直接相加呢?
这是个值得思考的问题,翻阅知乎
transformer中使用的position embedding为什么是加法?
随后我看了李宏毅老师的视频,他举了一个例子和这个有些不太一样,它是将embedding前的x与one-hot的位置编码相加,最后进行embedding,可以证明和embedding后再相加是等效的。
但是这里是两个截然不同性质的变换,词嵌入是可以理解成与一个W矩阵相乘,但是正弦编码并不是,所以我觉得他们的相加并不能用上面的内容解释。
随后我找到了另一个
为什么 Bert 的三个 Embedding 可以进行相加?
本文的作者将input和positional embedding拆开得到了更好的结果,所以其实这里应该是个开放的问题,到底进行concat还是相加还是有待于优化,这里我们还是用原文中的直接相加。
正弦编码有以下优势:
1. 1. 1.有界,不会因为句子太长而导致输入值太大
2. 2. 2.两个位置的编码距离和句子总长度应该无关,比如如果选取第一个词编码为 0 0 0,最后一个词编码为 1 1 1,造出这样一个等差数列,那么不同长度句子中,中间都隔了 k k k个单词的两个单词,它们的编码距离会不一样,这样的坏处很明显,就比如句子2只是在句子1的后面直接append一些内容,那么在分析前面公共部分的内容时,由于编码问题会计算出不同的结果
3. 3. 3.我们选择正弦曲线函数,因为我们假设它能让模型很容易地学习关注相对位置,因为对于任何固定的偏移量 k k k, P E p o s + k PE_{pos+k} PEpos+k可以表示成 P E p o s PE_{pos} PEpos的线性函数,如下所示。
P E ( P E( PE( pos + k , 2 i ) = P E ( +k, 2 i)=P E( +k,2i)=PE( pos, 2 i ) P E ( k , 2 i + 1 ) + P E ( 2 i) P E(k, 2 i+1)+P E( 2i)PE(k,2i+1)+PE( pos, 2 i + 1 ) P E ( k , 2 i ) 2 i+1) P E(k, 2 i) 2i+1)PE(k,2i)
P E ( p o s + k , 2 i + 1 ) = P E ( p o s , 2 i + 1 ) P E ( k , 2 i + 1 ) − P E ( p o s , 2 i ) P E ( k , 2 i ) P E(p o s+k, 2 i+1)=P E(p o s, 2 i+1) P E(k, 2 i+1)-P E(p o s, 2 i) P E(k, 2 i) PE(pos+k,2i+1)=PE(pos,2i+1)PE(k,2i+1)−PE(pos,2i)PE(k,2i)
这个线性组合我这种小白只能简单意会一下,确实有道理。
4. 4. 4.这个公式的振幅是随维度递减的,其实我们可以考察 s i n ( p o s / k ) sin(pos/k) sin(pos/k)这样一个函数, k k k太大会导致相邻单词差异太小, k k k太小会导致经常突破周期而出现不同距离的差异相同的情况,于是这个公式应该相当于把 k k k太大和太小的情况分配到了不同的维度。
接下来实现:
class PositionalEndoing(nn.Module):
def __init__(self,d_model,dropout,max_len=5000):
#dropout为置0比率
super().init()
self.dropout=nn.Dropout(p=dropout)
pe=torch.zeros(max_len,d_model)
#位置编码矩阵
#行数:句子长度,列数:词嵌入维度
position=torch.arange(0,max_len).unsqueeze(1)
#max_len*1的绝对位置矩阵
div_term=torch.exp(torch.arange(0,d_model,2)*-(math.log(10000.0)/d_model)).unsqueeze(0)
#1*(d_model/2)的矩阵
pe[:,0::2]=torch.sin(position*div_term)
pe[:,1::2]=torch.cos(position*div_term)
#正弦位置编码
pe=pe.unsqueeze(0)
self.register_buffer('pe',pe)
#作用是训练时不会被更新,但保存模型时会被被保存
def forward(self,x):
x=x+Variable(self.pe[:,:x.size(1)],requires_grad=False)
#只需要截取pe中和x等长的前面一部分
#requires_grad=False代表不需要参与梯度下降的计算即不会更新
return self.dropout(x)
d_model=512
dropout=0.1
max_len=60
x=embr
#embr是上面进行词嵌入算出的2*4*512的张量,也就是输入
pe=PositionalEndoing(d_model,dropout,max_len)
pe_result=pe(x)
#计算出输入x对应的正弦编码
print(pe_result)
print(pe_result.shape)
输出结果:
tensor([[[-31.2595, 0.0000, 48.9006, ..., 33.8873, -6.0268, 21.1344],
[-14.9837, -16.0285, -64.5251, ..., -1.9540, -23.0337, 21.6329],
[ 19.6901, 56.6698, 33.2170, ..., 5.3528, 64.3326, 27.0896],
[-28.4203, -8.5853, -67.1757, ..., -46.9936, -9.5096, -13.5523]],
[[ 39.8861, 37.7924, 0.0000, ..., -44.0664, 1.1308, 5.2654],
[ 13.6493, 0.0000, -13.5862, ..., -28.0645, -19.7625, 36.2756],
[ 21.7883, 25.2173, 39.7321, ..., 0.0000, 17.3264, -17.0182],
[ 1.2813, -48.3587, -5.3715, ..., 23.1472, 5.8235, -34.8474]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
掩码
def subsequent_mask(size):
attn_shape=(1,size,size)
subsequent_mask=np.triu(np.ones(attn_shape),k=1).astype('uint8')
return torch.from_numpy(1-subsequent_mask)
print(subsequent_mask(5))
输出:
tensor([[[1, 0, 0, 0, 0],
[1, 1, 0, 0, 0],
[1, 1, 1, 0, 0],
[1, 1, 1, 1, 0],
[1, 1, 1, 1, 1]]], dtype=torch.uint8)
这里就是造出一个特定维度的下三角矩阵
注意力机制
A t t e n t i o n ( Q , K , V ) = softmax ( Q K T d k ) V Attention (Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V Attention(Q,K,V)=softmax(dkQKT)V
Q : Q u e r y Q:Query Q:Query,指询问
K : K e y K:Key K:Key,指关键词
V : V a l u e V:Value V:Value,指大脑对 K e y Key Key的延伸
Q Q Q是一个询问 m ∗ n ∗ k m*n*k m∗n∗k的询问,其中 m m m为句子数量, n n n为句子中的词向量数, k k k为词向量维度。
公式通俗来讲是表示 Q u e r y Query Query在 K e y Key Key和 V a l u e Value Value下的表示
大脑通常会先抓住最关键的部分,然后进行判断,这个公式就很显然放大了 K e y Key Key的作用,从询问中抓住 K e y Key Key,再用大脑进行反应。
关于这里为什么除以 d k \sqrt{d_{k}} dk,继续翻阅知乎
transformer中的attention为什么scaled?
给出了很好的解答,这里就不再重复搬运,总之是保持了期望和方差,使得避免出现梯度消失的问题(即更新步长极小)。
自注意力机制
在自注意力机制中
query=key=value=pe_result
也就是都等于编码后的输入
def attention(query,key,value,mask=None,dropout=None):
d_k=query.size(-1)
#query最后一个维度即为词嵌入维度
#query和key的转置相乘
scores=torch.matmul(query,key.transpose(-2,-1))/math.sqrt(d_k)
#query为n*m*k的张量,n表示询问数量,m表示词,k为词向量维度
if mask is not None:
scores=scores.masked_fill(mask==0,1e-9)
#将掩码为0的地方改成很小的数
p_attn=F.softmax(scores,dim=-1)
#对每一行的元素进行softmax函数
return torch.matmul(p_attn,value),p_attn
query=key=value=pe_result
#mask=Variable(torch.zeros(2,4,4))
attn,p_attn=attention(query,key,value,mask=None)
print(attn)
print(p_attn)
输出:
tensor([[[-17.6411, 0.0000, 7.2360, ..., 13.1555, -9.3508, -24.8513],
[ 17.0477, -50.4984, 4.5038, ..., -31.4088, -33.7503, 50.9418],
[-23.6287, 0.0000, 0.0000, ..., -21.6497, 49.8315, -22.8535],
[-41.4043, 21.7469, -10.9893, ..., -22.0963, -20.8806, -19.5988]],
[[-40.4908, 37.1446, 33.6379, ..., -12.9449, 27.1569, -21.3525],
[ -8.9225, 0.0000, -7.7905, ..., 11.8503, 13.9525, -13.2107],
[ 53.1293, 30.7136, -17.0468, ..., -13.0081, 4.9770, 14.0668],
[ 0.6563, -11.4418, -13.1637, ..., 8.1173, -66.3848, 31.4784]]],
grad_fn=<UnsafeViewBackward0>)
tensor([[[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]],
[[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]]], grad_fn=<SoftmaxBackward0>)
这里p_attn几乎是对角线全1,其原因是自注意力机制中query=key,所以就成了 A A T AA^T AAT,所以对角线上的值都是平方和,再经过 s o f t m a x softmax softmax放大后导致全被对角线所占据。
但是传入全 0 0 0的mask之后,scores值也会变为全 0 0 0,那么结果就会变得比较平均
attn,p_attn=attention(query,key,value,mask=mask)
输出:
tensor([[[ -0.1459, -1.1696, 2.8356, ..., -3.9629, 1.1271, 0.0543],
[ -0.1459, -1.1696, 2.8356, ..., -3.9629, 1.1271, 0.0543],
[ -0.1459, -1.1696, 2.8356, ..., -3.9629, 1.1271, 0.0543],
[ -0.1459, -1.1696, 2.8356, ..., -3.9629, 1.1271, 0.0543]],
[[ 14.1035, 15.4130, -6.2358, ..., 3.1834, -11.2873, 17.8793],
[ 14.1035, 15.4130, -6.2358, ..., 3.1834, -11.2873, 17.8793],
[ 14.1035, 15.4130, -6.2358, ..., 3.1834, -11.2873, 17.8793],
[ 14.1035, 15.4130, -6.2358, ..., 3.1834, -11.2873, 17.8793]]],
grad_fn=<UnsafeViewBackward0>)
tensor([[[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]],
[[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500],
[0.2500, 0.2500, 0.2500, 0.2500]]], grad_fn=<SoftmaxBackward0>)
多头注意力机制
这里简而言之就是将词向量的维度分配给多个head,从而有种均摊误差的效果(不在一棵树上吊死),并且对Q,K,V都进行了不同的线性组合(Linear)使它们都变为大小相同但值不同的方阵,中间进行了维度的转置,大概意思写在注释中,最后一步view重新变为了三维张量其实就是把head个矩阵进行了concat,最后经过一个线性层进行输出。
def clones(moudule,N):
return nn.ModuleList([copy.deepcopy(moudule) for _ in range(N)])
#深复制
class MultiHeadedAttention(nn.Module):
def __init__(self,head,embedding_dim,dropout=0.1):
#head代表头数,embedding_dim代表词嵌入维度,dropout置零比率
super().__init__()
assert embedding_dim%head==0
#embedding_dim需要能整除head
self.d_k=embedding_dim//head
#词嵌入维度平均分给每一个head
self.head=head
self.linears=clones(nn.Linear(embedding_dim,embedding_dim),4)
#Linear的两个参数分别对应输入和输出,这里也就是一个embedding_dim*embedding_dim的矩阵
#linears就是四个这样的模型组成的列表
#4个是指Q,K,V各需要一个,最后concat之后还需要一个linear
self.attn=None
#注意力张量
self.dropout=nn.Dropout(p=dropout)
def forward(self,query,key,value,mask=None):
if mask is not None:
mask=mask.unsqueeze(0)
batch_size=query.size(0)
#query的第一维的大小其实也就是batch_size
query,key,value=\
[model(x).view(batch_size,-1,self.head,self.d_k).transpose(1,2)
for model,x,in zip(self.linears,(query,key,value))]
#zip用于进行linear和QKV一对一的遍历
#关于尺寸,batch_size不用说,head*d_k=embedding_dim,剩下一个维度自然就是词的数量也就是句子长度
#进行转置可以让句长维度和词向量维度更加接近,让head成为外层索引
#整体来讲就是对QKV各自进行一次线性变换各自变为一个方阵,再重塑尺寸
#让多头分担词汇不同的特征部分,从而减少误差,让词义有更加多元的表达
x, self.attn = attention(query, key, value, mask, self.dropout)
#x也就是输出
#attn为权重矩阵
x=x.transpose(1,2).contiguous().view(batch_size,-1,self.head*self.d_k)
return self.linears[-1](x)
#最后一个linear
head=8
embedding_dim=512
dropout=0.2
query=key=value=pe_result
mask=Variable(torch.zeros(8,4,4))
mha=MultiHeadedAttention(head,embedding_dim,dropout)
mha_result=mha(query,key,value)
输出:
tensor([[[ 5.6266, 2.4875, 8.4517, ..., -6.7918, 2.5055, 5.9314],
[ -6.5806, 3.0218, 15.3889, ..., 0.8658, -18.9831, 21.2460],
[-14.5902, -10.0083, -7.1232, ..., -2.4021, -17.7752, 0.6481],
[ 14.2960, -7.5041, 0.3042, ..., -11.6881, -7.5634, -14.6501]],
[[-13.5806, -6.2719, 0.2771, ..., -0.5751, -5.6179, -8.9107],
[ -4.6952, -15.1235, -19.1021, ..., 3.2530, 8.1995, 4.5777],
[ -6.2927, 3.8340, -18.3732, ..., 9.6667, 3.2841, 8.2817],
[ 0.6177, -8.6816, -13.9586, ..., -2.3969, 0.5891, -4.4065]]],
grad_fn=<AddBackward0>)
torch.Size([2, 4, 512])
输入层的核心已经结束了,接下来就是一些数值处理的操作
前馈全连接层
对应图中的Feed Forward模块
这里它是用的全连接网络,中间用了一次relu作为激活函数,为什么这么操作我也不清楚,可能实验效果比较好吧,总之就是先线性变换一次,再relu,再线性变换一次
class PositionwiseFeedForward(nn.Module):
def __init__(self,d_model,d_ff,dropout=0.1):
#d_ff是词嵌入维度
super().__init__()
self.w1=nn.Linear(d_model,d_ff)
self.w2=nn.Linear(d_ff,d_model)
self.dropout=nn.Dropout(dropout)
def forward(self,x):
return self.w2(self.dropout(F.relu(self.w1(x))))
#relu计算简单,而且不容易出现梯度爆炸和梯度消失
d_model=512
d_ff=64
dropout=0.2
x=mha_result
ff=PositionwiseFeedForward(d_model,d_ff,dropout)
ff_result=ff(x)
print(ff_result)
输出:
tensor([[[-0.0842, -2.3390, -0.3861, ..., -1.1567, 0.6501, 0.6989],
[ 2.2971, -1.0878, 0.4681, ..., -4.3583, 0.6660, 4.5701],
[-1.1708, 1.3941, -0.1086, ..., -0.8627, -0.4052, -1.6384],
[-0.3328, -1.8596, -0.3813, ..., -2.4343, -0.2367, -1.6852]],
[[ 1.7638, -1.5655, 2.5129, ..., -4.1856, -0.9209, -0.4936],
[ 2.1474, -3.6081, 0.7268, ..., -1.7562, -0.7775, 1.6036],
[ 2.6642, -4.3401, -0.9985, ..., -0.5323, -2.1452, 1.8985],
[-3.5607, -1.7900, 1.6536, ..., -2.1132, -0.2075, 3.9405]]],
grad_fn=<AddBackward0>)
torch.Size([2, 4, 512])
规范化层
这里顾名思义就是规范化一下,减去均值除以方差,弄出个符合正太分布的x’,然后进行a2x’+b2的操作,这里x’是个 2 ∗ 4 ∗ 512 2*4*512 2∗4∗512的方阵而a2是个 512 512 512大小的数组,所以权重是给 512 512 512个词向量维度分配的,很合理。
class LayerNorm(nn.Module):
def __init__(self,features,eps=1e-6):
super().__init__()
self.a2=nn.Parameter(torch.ones(features))
self.b2 = nn.Parameter(torch.zeros(features))
#用Parameter封装的参数会加入训练
self.eps=eps
def forward(self,x):
mean=x.mean(-1,keepdim=True)
#以最后一个维度求均值,keepdim保持维度,如5*5的矩阵不加这个参数求平均值后会
#直接变为5,加了就是5*1
std=x.std(-1,keepdim=True)
#计算标准差
return self.a2*(x-mean)/(std+self.eps)+self.b2
#减均值除标准差得到x',再计算a2*x'+b2
#得到x'也就是标准差标准化,经过处理的数据符合正态分布
#注意这里不是矩阵乘法,是对应位置相乘
features=d_model=512
eps=1e-6
x=ff_result
ln=LayerNorm(features,eps)
ln_result=ln(x)
print(ln_result)
print(ln_result.shape)
输出:
tensor([[[ 0.3937, -1.5343, 0.3623, ..., 0.9180, 0.8813, -0.1429],
[ 0.2394, -0.3429, 0.2586, ..., -0.0660, 2.0112, 0.7106],
[-0.0393, -0.3831, 0.0272, ..., -2.4721, 1.0900, 1.0801],
[-0.4783, -1.0320, -1.7881, ..., 0.4728, 0.1609, -0.2272]],
[[ 0.2892, 0.2732, -0.8153, ..., 0.2160, 1.2437, -2.5539],
[-0.6363, -0.8620, 0.2009, ..., -0.3676, 0.3137, 1.2609],
[-0.1761, -0.2589, -1.3003, ..., -1.1288, 0.6398, 0.6090],
[-0.0082, -0.6592, 0.0573, ..., 0.2271, 0.3160, -0.8449]]],
grad_fn=<AddBackward0>)
torch.Size([2, 4, 512])
子层连接结构
这个部分不出意外的话视频里应该是出问题了,翻阅文献和网上的解析应该是LayerNorm(x+sublayer(x))
sublayer可以是上图的multi-head也可以是feed forward
相加之后最后一起规范化
class SublayerConnection(nn.Module):
def __init__(self,size,dropout=0.1):
super().__init__()
self.norm=LayerNorm(size)
self.dropout=nn.Dropout(p=dropout)
def forward(self,x,sublayer):
return self.dropout(self.norm(x+sublayer(x)))
#sublayer是子层,这里的子层是指feed forward和multihead
size=512
dropout=0.2
head=8
d_model=512
x=pe_result
mask=Variable(torch.zeros(8,4,4))
self_attn=MultiHeadedAttention(head,d_model)
sublayer=lambda x: self_attn(x,x,x,mask)
sc=SublayerConnection(size,dropout)
sc_result=sc(x,sublayer)
print(sc_result)
print(sc_result.shape)
做了这样一个类之后,就可以将子层函数如multihead和feed forward作为参数传入,就实现了上图的两个残差连接的模块,相当于一个函数模板。
输出:
tensor([[[ 0.5021, -0.0722, 1.8054, ..., -0.0082, -1.3347, -2.0638],
[-0.5705, 0.0000, 3.9156, ..., -0.0000, -0.0898, 0.0000],
[-1.6755, 0.1052, 1.0844, ..., -0.8102, -2.6503, 0.6323],
[-0.6072, -0.0875, -0.0000, ..., -0.2794, -0.3621, -1.0605]],
[[-2.1169, 0.0139, 0.0000, ..., -0.8220, 0.0000, -1.3642],
[-1.6420, 1.9355, -0.6514, ..., 0.0000, -0.5959, 0.6231],
[-0.2153, 2.4281, -1.3161, ..., 0.0000, -0.0000, -1.8842],
[-1.2555, 1.2043, -0.5352, ..., -0.1091, -0.0000, 1.0707]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
编码器层
编码器其实就是把上面的两个子层连接结构简单封装成一个EncoderLayer类
class EncoderLayer(nn.Module):
def __init__(self,size,self_attn,feed_forward,dropout):
super().__init__()
self.self_attn=self_attn
self.feed_forward=feed_forward
self.sublayer=clones(SublayerConnection(size,dropout),2)
self.size=size
def forward(self,x,mask):
x=self.sublayer[0](x,lambda x:self.self_attn(x,x,x,mask))
return self.sublayer[1](x,self.feed_forward)
size=512
head=8
d_model=512
d_ff=64
x=pe_result
dropout=0.2
self_attn=MultiHeadedAttention(head,d_model)
ff=PositionwiseFeedForward(d_model,d_ff,dropout)
mask=Variable(torch.zeros(8,4,4))
输出:
tensor([[[-0.1981, -0.0000, 1.1597, ..., -0.1466, -2.9241, 0.2823],
[ 0.4510, -1.2408, 0.1163, ..., 0.0000, -1.8986, -0.7663],
[-0.3029, 0.1413, 0.0000, ..., 2.1100, -2.4588, -0.6241],
[ 0.6345, -0.0330, -2.3838, ..., 0.0767, -0.0000, -1.3296]],
[[ 0.1341, -0.3915, 2.3283, ..., 0.0000, 0.0000, 0.9070],
[ 0.0000, -3.0416, 0.7024, ..., -0.2680, 1.0492, 0.3752],
[ 0.0000, -0.2520, 0.0000, ..., -0.4895, -0.4272, 1.7757],
[ 0.4344, -0.1694, -2.0037, ..., 0.0408, -1.1797, 0.3375]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
编码器
依然是继续封装,编码器就是编码器层*N
class Encoder(nn.Module):
def __init__(self,layer,N):
super().__init__()
self.layers=clones(layer,N)
def forward(self,x,mask):
for layer in self.layers:
x=layer(x,mask)
return x
size=512
head=8
d_model=512
d_ff=64
c=copy.deepcopy
attn=MultiHeadedAttention(head,d_model)
ff=PositionwiseFeedForward(d_model,d_ff,dropout)
dropout=0.2
layer=EncoderLayer(size,c(attn),c(ff),dropout)
N=8
mask=Variable(torch.zeros(8,4,4))
en=Encoder(layer,N)
en_result=en(x,mask)
print(en_result)
print(en_result.shape)
这里依然写得和视频里不一样,因为上面改过的编码器层最后已经规范化过了
输出:
tensor([[[ 0.4498, 1.0731, -0.7424, ..., -0.0000, -1.8726, 1.6560],
[-0.3369, 0.9220, -0.3264, ..., -0.1954, -1.5015, -0.0000],
[-0.3725, -2.8675, 1.2287, ..., 0.0761, 2.3905, 0.3090],
[-0.2990, 0.2441, 0.3848, ..., 1.8894, 0.0735, 1.2151]],
[[ 0.1298, 1.0290, -0.6615, ..., -0.5989, -0.0063, 0.0000],
[-0.7160, -0.0830, -0.9277, ..., 0.0000, -0.0000, -0.6709],
[ 0.8316, -0.9386, -0.3482, ..., -0.0000, 0.5017, -0.3504],
[ 1.7595, 1.2951, 2.7818, ..., -0.1398, -2.9854, -0.6698]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
解码器层
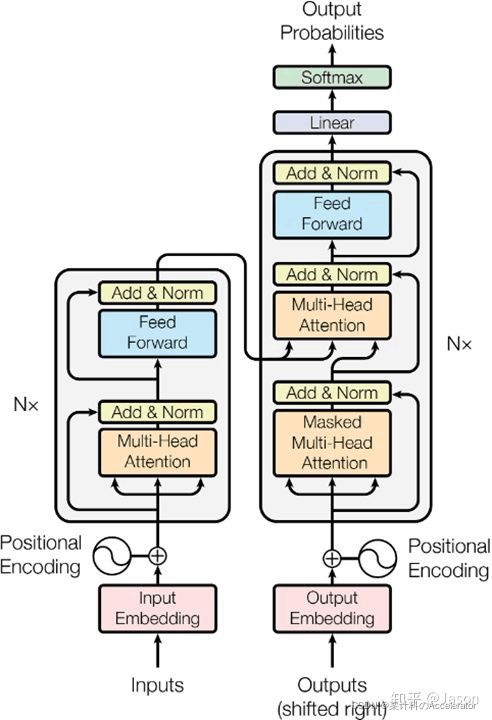
回归到这张图,我们已经完成了左边的部分,右边的outputs就相当于input需要对应的target,它会先经由一个masked的multi-head attention,这里总算用上了我们之前写的掩码,它的作用是,对于一个句子中的每一个词语,遮蔽这个词后面的词的信息,也就是将未来的信息给mask掉
这样也就是
A i j = 1 ( i < n , j < = i ) A_{ij}=1(i
于是就形成了一个下三角矩阵
然后再往上一层,其实decoder会接收encoder左侧传过来的参数,这里是作为 K K K和 V V V,decoder提供的参数作为 Q Q Q,这里这么做的原因就相当于接收编码器的输出信息来计算机当前解码应该输出什么,也就是key和value来自于编码器,query来自于output,这里有点套娃的感觉,自然输出结果就是query在key和value下的注意力张量,感觉相当于output在input下的注意力张量。(其实也是有点云里雾里的这一块,先这样吧)
class DecoderLayer(nn.Module):
def __init__(self,size,self_attn,src_attn,feed_forward,dropout):
super().__init__()
self.size=size
self.self_attn=attn
self.src_attn=self_attn
self.feed_forward=feed_forward
self.sublayer=clones(SublayerConnection(size,dropout),3)
def forward(self,x,memory,source_mask,target_mask):
m=memory
x=self.sublayer[0](x,lambda x:self.self_attn(x,x,x,target_mask))
x=self.sublayer[1](x,lambda x:self.src_attn(x,m,m,source_mask))
#这里的source_mask用来遮蔽掉对结果没有意义的字符的注意力值
return self.sublayer[2](x,self.feed_forward)
head=8
size=512
d_model=512
d_ff=64
dropout=0.2
self_attn=src_attn=MultiHeadedAttention(head,d_model)
ff=PositionwiseFeedForward(d_model,d_ff,dropout)
x=pe_result
memory=en_result
mask=Variable(torch.zeros(8,4,4))
target_mask=subsequent_mask(4)
source_mask=mask
dl=DecoderLayer(size,self_attn,src_attn,ff,dropout)
dl_result=dl(x,memory,source_mask,target_mask)
print(dl_result)
print(dl_result.shape)
输出:
tensor([[[ 0.0252, -2.1165, 0.2505, ..., -0.1514, -3.6794, 3.0512],
[-0.2031, 0.1044, 0.1536, ..., -0.6930, 0.0000, -1.3079],
[ 4.1483, -1.5894, -0.6305, ..., 1.3983, -1.2923, 1.3873],
[-0.5289, 1.4646, -0.2385, ..., 0.4411, 2.8952, -0.0944]],
[[ 2.2889, 0.0000, -0.0616, ..., -0.0000, -1.0136, 1.3932],
[ 0.0000, -0.2390, -0.0000, ..., 0.2183, -0.0000, 0.0000],
[-0.2049, -3.3786, 0.5995, ..., 0.0000, -2.6760, 3.1795],
[-2.3916, 2.9400, -1.6383, ..., 0.0401, -0.2806, -0.0000]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
解码器
就是对上面进行*N封装了
class Decoder(nn.Module):
def __init__(self,layer,N):
super().__init__()
self.layers=clones(layer,N)
def forward(self,x,memory,source_mask,target_mask):
for layer in self.layers:
x=layer(x,memory,source_mask,target_mask)
return x
size=512
d_model=512
head=8
d_ff=64
dropout=0.2
c=copy.deepcopy
attn=MultiHeadedAttention(head,d_model)
ff=PositionwiseFeedForward(d_model,d_ff,dropout)
layer=DecoderLayer(d_model,c(attn),c(attn),c(ff),dropout)
N=8
x=pe_result
memory=en_result
mask=Variable(torch.zeros(8,4,4))
target_mask=subsequent_mask(4)
source_mask=mask
de=Decoder(layer,N)
de_result=de(x,memory,source_mask,target_mask)
print(de_result)
print(de_result.shape)
输出:
tensor([[[ 0.0000, 1.1949, -0.6378, ..., 0.2904, -0.4521, 0.0000],
[ 0.5356, 0.0653, -4.6251, ..., 1.7602, -0.0708, 0.0459],
[ 0.6124, 1.4326, -1.5422, ..., 1.5063, 0.9769, -0.0000],
[ 0.0000, -0.0000, -2.4902, ..., 0.6073, -0.2428, 0.0869]],
[[-0.7473, 0.6388, -1.2236, ..., -0.0265, -0.4547, -0.6132],
[ 0.0000, -0.0000, -0.0000, ..., -0.8934, -0.3948, -0.0000],
[ 0.3118, -0.0221, 0.1143, ..., -0.5320, -0.4980, 0.0000],
[ 0.0790, -0.2463, -0.7042, ..., -0.7297, -0.1085, 0.1360]]],
grad_fn=<MulBackward0>)
torch.Size([2, 4, 512])
输出部分
class Generator(nn.Module):
def __init__(self,d_model,vcab_size):
super().__init__()
self.project=nn.Linear(d_model,vocab)
def forward(self,x):
return F.softmax(self.project(x),dim=-1)
x=de_result
gen=Generator(d_model,vocab)
gen_result=gen(x)
print(gen_result)
print(gen_result.shape)
输出:
tensor([[[0.0018, 0.0002, 0.0011, ..., 0.0009, 0.0029, 0.0014],
[0.0021, 0.0027, 0.0014, ..., 0.0015, 0.0006, 0.0010],
[0.0004, 0.0010, 0.0010, ..., 0.0011, 0.0009, 0.0002],
[0.0011, 0.0019, 0.0014, ..., 0.0011, 0.0008, 0.0010]],
[[0.0004, 0.0004, 0.0053, ..., 0.0007, 0.0014, 0.0011],
[0.0005, 0.0004, 0.0015, ..., 0.0004, 0.0009, 0.0006],
[0.0009, 0.0004, 0.0014, ..., 0.0003, 0.0020, 0.0005],
[0.0018, 0.0007, 0.0016, ..., 0.0005, 0.0005, 0.0006]]],
grad_fn=<SoftmaxBackward0>)
torch.Size([2, 4, 1000])
结语
到此为止output probabilities已经被成功地输出了,也就是模型的基本搭建完成,接下来无非就是根据loss训练啥的了,可能不会再继续深究,大致理解就好了,后面肯定是直接调python的transformer库了。