激活函数之softmax函数
1.softmax函数
分类问题中使用的 softmax 函数可以用下面的式表示:
![]()
exp(x ) 是表示 ex 的指数函数(e 是纳皮尔常数 2.7182 …)。式(3.10)表示假设输出层共有 n 个神经元,计算第 k 个神经元的输出 yk 。如式(3.10)所示,softmax 函数的分子是输入信号 ak 的指数函数,分母是所有输入信号的指数函数的和。
import numpy as np
def softmax(x):
exp_a = np.exp(x)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
if __name__ == '__main__':
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
print(np.exp(0.3) / np.sum(np.exp(a)))
b = np.array([1010, 1000, 990])
h = softmax(b)
print(h)
执行结果:
F:/Keras/numpy_excl/excl_1.py:5: RuntimeWarning: overflow encountered in exp
exp_a = np.exp(x)
F:/Keras/numpy_excl/excl_1.py:7: RuntimeWarning: invalid value encountered in true_divide
y = exp_a / sum_exp_a
[0.01821127 0.24519181 0.73659691]
0.018211273295547534
[nan nan nan]
上面的 softmax 函数的实现虽然正确描述了式(3.10),但在计算机的运算上有一定的缺陷。这个缺陷就是溢出问题。softmax 函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大。比如,e10 的值会超过 20000,e100 会变成一个后面有 40 多个 0 的超大值,e1000 的结果会返回一个表示无穷大的 inf 。如果在这些超大值之间进行除法运算,结果会出现“不确定”的情况。
计算机处理“数”时,数值必须在 4 字节或 8 字节的有限数据宽度内。这意味着数存在有效位数,也就是说,可以表示的数值范围是有限的。因此,会出现超大值无法表示的问题。这个问题称为溢出,在进行计算机的运算时必须(常常)注意。
softmax 函数的实现可以像式(3.11)这样进行改进。
2.改进softmax函数
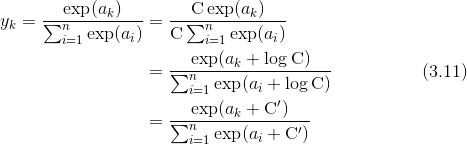
首先,式(3.11)在分子和分母上都乘上 C 这个任意的常数(因为同时对分母和分子乘以相同的常数,所以计算结果不变)。然后,把这个 C 移动到指数函数(exp)中,记为 log C。最后,把 log C 替换为另一个符号 C’ 。
式(3.11)说明,在进行 softmax 的指数函数的运算时,加上(或者减去)某个常数并不会改变运算的结果。这里的 C’ 可以使用任何值,但是为了防止溢出,一般会使用输入信号中的最大值。
import numpy as np
def softmax(x):
c=np.max(x)
exp_a = np.exp(x-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
if __name__ == '__main__':
a = np.array([0.3, 2.9, 4.0])
y = softmax(a)
print(y)
print(np.exp(0.3) / np.sum(np.exp(a)))
b = np.array([1010, 1000, 990])
h = softmax(b)
print(h)
print(np.exp(1010 - 1010) / np.sum(np.exp(b - 1010)))
运行结果:
[0.01821127 0.24519181 0.73659691]
0.018211273295547534
[9.99954600e-01 4.53978686e-05 2.06106005e-09]
0.999954600070331
如上所示,softmax 函数的输出是 0.0 到 1.0 之间的实数。并且,softmax 函数的输出值的总和是 1。输出总和为 1 是 softmax 函数的一个重要性质。正因为有了这个性质,我们才可以把 softmax 函数的输出解释为“概率”。