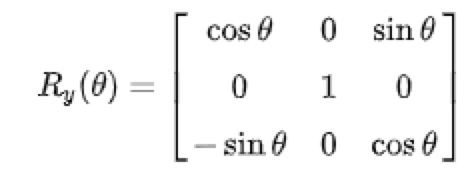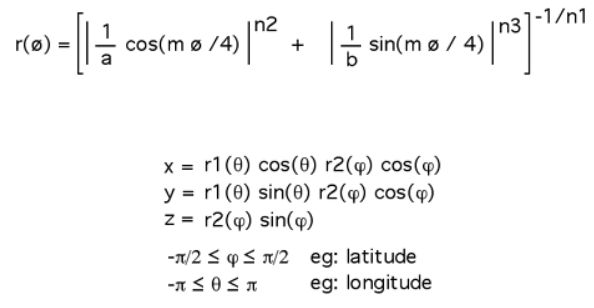画球大师教你如何画好一个球

作者 | 翁鹏

 42

如何画个球？好像 JS 和 CSS 并没有提供这个能力，当然也不可能为了画个球引入 Threejs。这篇文章将介绍 4 种画球的方法，每种方法都有不同的特点，生成球的数据可以使用任何方式渲染，可以在 canvas 中渲染，也可以使用 DOM 来渲染来实现一些博客里面的标签球效果。文章的最后将结合前面的知识，来画出更加复杂酷炫的 3D 形状。

标准球

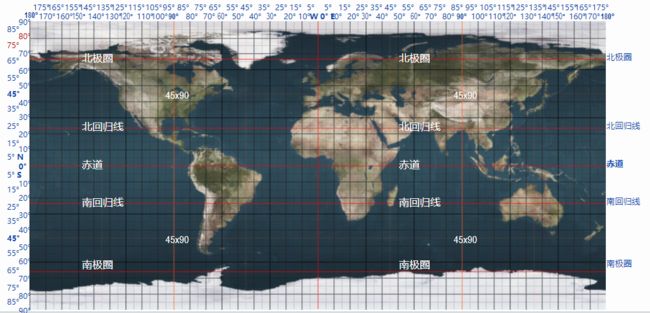
标准球也称为 UV Sphere，它是最常用的画球方法。要了解它首先来看下常见的地球平面图。

从这张图可以看到，经线是列，从东经 180° 到西经 180°，纬线是行从北纬 90° 到南纬 90°。经线和纬线交叉形成一个个小格子，我们获取网格上的顶点，在使用 Spherical coordinate system 把它变成 3 维球体坐标就行了。打开这篇文章，可以找到下面这个公式。

其中 r 是半径，Theta 是纬度，Phi 是经度。知道了上面的公式就可以来画球了。

function createSphere(total = 10) {
	const points = []
    let lat, lon, x, y, z
    for (let i = 0; i <= total; ++i) {
    	lat = i * Math.PI / total // 纬度
    	for (let j = 0; j <= total; ++j) {
          lon = j * 2 * Math.PI / total // 经度
          x = Math.sin(lat) * Math.cos(lon)
          y = Math.sin(lat) * Math.sin(lon)
          z = Math.cos(lat)
          // 为了方便对应观看，把一些可以在第一层循环计算的公式放入这层，会有点重复计算
          points.push([x, y, z])
        }
    }
    return points
}

用 total 表示经线和纬线的数量，通过公式求出网格上的每个点的位置。这里缺少了公式中的 r，是因为希望返回的是单位球，所以这里 r 等于 1 就忽略了。默认是 10 条经线和纬线，当经线和纬线越来越大时，生成的球的表面也就越光滑。

有了这些数据我们就可以使用各种方式渲染。

用 canvas 渲染

const canvas = document.createElement('canvas')
canvas.width = 800; canvas.height = 800
document.body.appendChild(canvas)

const ctx = canvas.getContext('2d')
const points = createSphere()

ctx.clearRect(0, 0, canvas.width, canvas.height)
ctx.save();
ctx.lineWidth = 5 / canvas.width
ctx.translate(canvas.width / 2, canvas.height / 2) // 移动到中间
ctx.scale(canvas.width / 5, canvas.height / 5) // 放大
ctx.beginPath()
ctx.moveTo(xys[0][0], xys[0][1])
for (let i = 1, l = xys.length; i < l; i++) {
  ctx.lineTo(xys[i][0], xys[i][1])
}
ctx.stroke(); ctx.restore()

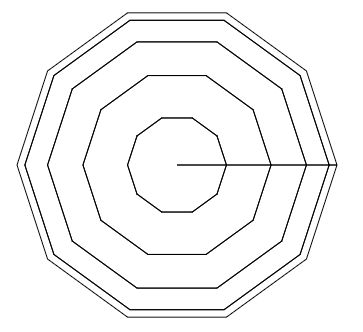
通过上图可以发现是球的两极对准我们，但是我们希望两极在 Y 轴上。

function createSphere(total = 10) {
//.......
          x = Math.sin(lat) * Math.cos(lon)
          y = Math.sin(lat) * Math.sin(lon)
          z = Math.cos(lat)
          points.push([y, z, x]) // 更换位置
//.......
}

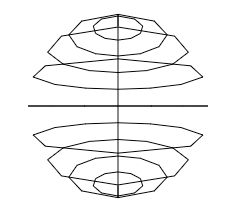
通过更换 x, y, z 的位置将两极放到了 Y 轴上。不过现在还没有透视效果，看不出来是个球体，下面来添加透视效果。

const xys = points.map((point) => {
  const x = point[0], y = point[1], z = point[2]
  const zToD = 2 - z
  return [x / zToD, y / zToD]
})
// ...............
ctx.moveTo(xys[0][0], xys[0][1])
for (let i = 1, l = xys.length; i < l; i++) {
  ctx.lineTo(xys[i][0], xys[i][1])
}

透视效果是近大远小，所以这里用 x 和 y 除 z。因为是单位圆 z 的值是 -1 到 1。2 - z 将 z 的值变为 1 到 3。这里的 2 其实是我们具体球的距离，当这个值越大时会发现球距离我们越来越远。

下面让球转起来吧。怎么让球旋转呢？同样打开 Wikipedia 找到 Rotation matrix 这篇文章，我们希望球绕 Y 轴旋转，可以找到下面这个旋转矩阵。

let rotate = 0
function draw() {
  ctx.clearRect(0, 0, canvas.width, canvas.height)
  ctx.save()
  ctx.lineWidth = 5 / canvas.width
  ctx.translate(canvas.width / 2, canvas.height / 2) // 移动到中间
  ctx.scale(canvas.width / 5, canvas.height / 5) // 放大
  const xys = points.map((point) => {
    const x = point[0] * Math.cos(rotate) + point[2] * Math.sin(rotate)
    const y = point[1]
    const z = -1 * point[0] * Math.sin(rotate) + point[2] * Math.cos(rotate)
    const zToD = 2 - z
    return [x / zToD, y / zToD]
  })
  ctx.beginPath()
  ctx.moveTo(xys[0][0], xys[0][1])
  for (let i = 1, l = xys.length; i < l; i++) {
    ctx.lineTo(xys[i][0], xys[i][1])
  }
  ctx.stroke()
  ctx.restore()
  rotate += 0.05
  requestAnimationFrame(draw)
}

这里增加了 total 的值，可以发现球更圆了。

用 CSS3 渲染

同样我们还可以用 CSS 来渲染，利用 CSS3 中的透视和 animation 等属性可以很方便的渲染出来。

body {
  font-size: 12px;
  perspective: 500px;
  overflow: hidden;
}

#app {
  width: 100vw;
  height: 100vh;
  transform-style: preserve-3d;
  animation: rot 5s linear infinite normal;
}

#app div {
  position: absolute;
  left: 50%;
  top: 50%;
}

@keyframes rot {
  100% { transform: rotateY(1turn); }
}

const points = createSphere()
const app = document.querySelector('#app')
const html = points.map((p, i) => {
  return `
${i}
`
})
app.innerHTML = html.join('')

仅仅只需要几行代码就渲染出来。但是可以发现球的两极有很多的点重叠，并且有两条经线重叠。

两极重复是因为第一行和最后一行的点都在两极，两条经线重复是因为上面公式中经线范围是 [0, 2PI) 它不包括 2PI。

function createSphere(meridians = 10, parallels = 10) {
  const points = []
  points.push([0, 1, 0]) // 手动填入第一行
  let lat, lon, x, y, z
  for (let i = 1; i < parallels; ++i) { // 少两行
      lat = i * Math.PI / parallels
      for (let j = 0; j < meridians; ++j) { // 少一列
        lon = j * 2 * Math.PI / meridians
        x = Math.sin(lat) * Math.cos(lon)
        y = Math.sin(lat) * Math.sin(lon)
        z = Math.cos(lat)
        points.push([y, z, x])
    }
  }
  points.push([0, -1, 0]) // 手动填入最后一行
  return points
}

这样就可以得到一个没有点重复顶点的球。

用 webgl 渲染

用 webgl 渲染，还需要修改一下 createSphere 方法，因为 webgl 中用的是主要用的是三角形，我们需要把每 3 个相关的点连接成一个三角形。

function createSphere(meridians = 10, parallels = 10) {
  let vertices = [], points = [];

  vertices.push([0, 1, 0])
  let lat, lon, x, y, z;
  for (let i = 1; i < parallels; ++i) {
    lat = i * Math.PI / parallels
    for (let j = 0; j < meridians; ++j) {
      lon = j * 2 * Math.PI / meridians
      x = Math.sin(lat) * Math.cos(lon)
      y = Math.sin(lat) * Math.sin(lon)
      z = Math.cos(lat)
      vertices.push([y, z, x])
    }
  }
  vertices.push([0, -1, 0])

  function tri(a, b, c) { // 添加三角形
    points.push(...vertices[a], ...vertices[b], ...vertices[c])
  }
  function quad(a, b, c, d) { // 将一个网格分成两个三角形
    tri(b, a, c)
    tri(b, c, d)
  }

  for (let i = meridians; i > 0; --i) { // 计算顶部三角形
    tri(0, i - 1 || meridians, i) // 当是最后一个时连接到第一个
  }
  let aStart, bStart
  for (let i = 0; i < parallels - 2; ++i) { // 计算中间网格三角形
    aStart = i * meridians + 1
    bStart = (i + 1) * meridians + 1
    for (let j = 0; j < meridians; ++j) {
      quad(aStart + j, aStart + (j + 1) % meridians, bStart + j, bStart + (j + 1) % meridians)
      // 当是最后一列是连接到第一列
    }
  }
  for (let l = vertices.length - 1, i = l - meridians; i < l; ++i) { // 计算底部三角形
    tri(l, i + 1 === l ? l - meridians : i + 1, i)
  }

  return new Float32Array(points)
}

上面我们手动处理了第一和最后一行。需要注意，当是最有一列时需要将最后一列连接到第一列。

const vs = `
  attribute vec4 a_position;
  uniform mat4 u_mvp;
  void main() {
    gl_Position = u_mvp * a_position;
  }
`
const fs = `
  precision mediump float;
  void main() {
    gl_FragColor = vec4(0.1, 0.8, 0.5, 1.);
  }
`
// 省略
let rotate = 0
const sphere = createSphere(15, 15)
const count = sphere.length / 3
function draw() {
  // 省略
  gl.drawArrays(gl.LINE_STRIP, 0, count);
  requestAnimationFrame(() => { rotate += 0.03; draw() })
}
draw()

因为 webgl 代码比较冗长，所以这里省略的大量相关代码，只保留了两个 shader 和最终渲染方法，详细代码可以查看

https://github.com/woopen/sphere。

正方体

还可以通过正方体来得到球形，这个正方体类似于魔方，它的每一个面都是一个网格。

首先要生成这个魔方，然后对上面的点进行归一化，这样就可以得到单位球。

要生成一个这个正方体，我们需要 3 层循环，循环正方体的每个面，每一行和每一列。我可以定义每个面的起点，右和上的终点，然后在每次循环中乘以对应步长，就可以得到这个正方体。

function createNormalizedCubeSphere(divisions = 5) {
  const vertices = [], points = []

  const origins = [
    [-1, -1, -1], [1, -1, -1], [1, -1, 1],
    [-1, -1, 1], [-1, 1, -1], [-1, -1, 1]
  ]
  const rights = [
    [2, 0, 0], [0, 0, 2], [-2, 0, 0],
    [0, 0, -2], [2, 0, 0], [2, 0, 0]
  ]
  const ups = [
    [0, 2, 0], [0, 2, 0], [0, 2, 0],
    [0, 2, 0], [0, 0, 2], [0, 0, -2]
  ]

  const step = 1 / divisions // 每一步的长度
  let origin, right, up
  for (let i = 0 ; i < 6; ++i) {
    origin = origins[i]
    right = rights[i]
    up = ups[i]
    for (let j = 0; j <= divisions; ++j) {
      for (let k = 0; k <= divisions; ++ k) {
        const ur = vec3.add([], vec3.scale([], up, j * step), vec3.scale([], right, k * step)) // 向右走和向上走的距离
        vertices.push(
          vec3.normalize([], vec3.add([], origin, ur)) // 起点加上这个距离，并归一化
        )
      }
    }
  }
  
  // 上面的已经生成这个球的所有顶点，但是要在 webgl 中渲染的话还需要三角化

  function tri(a, b, c) {
    points.push(...vertices[a], ...vertices[b], ...vertices[c])
  }
  function quad(a, b, c, d) {
    tri(b, a, c)
    tri(b, c, d)
  }

  const row = divisions + 1
  let a, c
  for (let i = 0; i < 6; ++i) {
    for (let j = 0; j < divisions; ++j) {
      for (let k = 0; k < divisions; ++k) {
      	// 获取每个小网格并生成两个三角形
        a = (i * row + j) * row + k
        c = (i * row + j + 1) * row + k
         quad(a, a + 1, c, c + 1)
      }
    }
  }

  return new Float32Array(points)
}

上面函数中的 vec3 代表三维向量，这里使用 glMatrix 来帮助我们进行向量运算。

同样可以使用 webgl 渲染，下图是细分 5 次后的结果。

正四面体细分

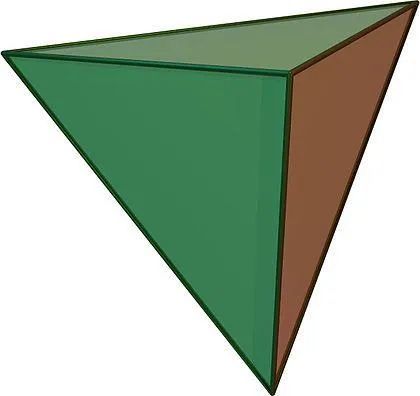
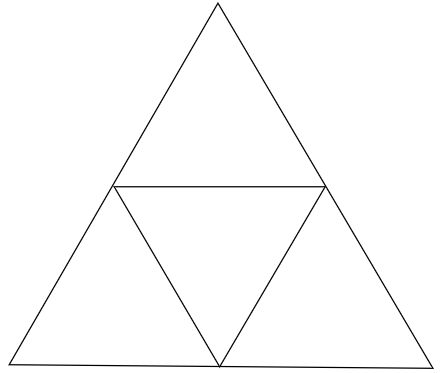
还可以通过对正四面体细分来近似球形。正四面体一共有 4 个面，每个面都是三角形。

通过细分每个面的三角形。通过获取一个三角形的每条边的中点，并连线，就可以生成 4 个小三角形，然后不断的重复这个过程不断的细分，最终将细分出来的点进行归一化就可以得到一个单位球。

可以通过这篇文章 Tetrahedron 知道正四面体的 4 个顶点的坐标。

function createTetrahedronSphere(count = 0) {
  const points = []

  const ta = [0, 0, -1]
  const tb = [Math.sqrt(8 / 9), 0, 1 / 3]
  const tc = [-1 * Math.sqrt(2 / 9), Math.sqrt(2/ 3), 1 / 3]
  const td = [-1 * Math.sqrt(2 / 9), -1 * Math.sqrt(2/ 3), 1 / 3]

  function tri(a, b, c) {
    points.push(...a, ...b, ...c)
  }
  function divide(a, b, c, count) {
    if (count > 0) {
      const ab = vec3.normalize([], vec3.scale([], vec3.add([], a, b), 0.5))
      const ac = vec3.normalize([], vec3.scale([], vec3.add([], a, c), 0.5))
      const bc = vec3.normalize([], vec3.scale([], vec3.add([], b, c), 0.5))
	  // 获取到每条边的中点，然后对其中的 4 个小三角形进行细分
      divide(a, ab, ac, count - 1)
      divide(ab, b, bc, count - 1)
      divide(bc, c, ac, count - 1)
      divide(ab, bc, ac, count - 1)
    } else {
      tri(a, b, c)
    }
  }

  // 细分 4 个面
  divide(ta, tc, tb, count)
  divide(ta, td, tc, count)
  divide(ta, tb, td, count)
  divide(tb, tc, td, count)

  return new Float32Array(points)
}

下图是细分 3 次后的结果。

正二十面体细分

正二十面体细分和正四面体细分非常相似。正四面体我们找出它的 4 个顶点，然后对它的 4 个面进行细分，正二十面体我们需要找到 12 个顶点，并对它 20 个面进行细分。既然和正四面体这么相似为什么不直接用正四面体多细分几次呢？这是因为正二十面体细分可以得到大小都一样的三角形球形。

通过这篇文章 Regular Icosahedron 可以了解正二十面体。

function createIcosahedronSphere(count = 0) {
  const points = []

  const t = (1 + Math.sqrt(5)) / 2
  const v1 = vec3.normalize([], [-1, t, 0])
  const v2 = vec3.normalize([], [1, t, 0])
  const v3 = vec3.normalize([], [-1, -t, 0])
  const v4 = vec3.normalize([], [1, -t, 0])
  const v5 = vec3.normalize([], [0, -1, t])
  const v6 = vec3.normalize([], [0, 1, t])
  const v7 = vec3.normalize([], [0, -1, -t])
  const v8 = vec3.normalize([], [0, 1, -t])
  const v9 = vec3.normalize([], [t, 0, -1])
  const v10 = vec3.normalize([], [t, 0, 1])
  const v11 = vec3.normalize([], [-t, 0, -1])
  const v12 = vec3.normalize([], [-t, 0, 1])

  function tri(a, b, c) {
    points.push(...a, ...b, ...c)
  }
  function divide(a, b, c, count) {
    if (count > 0) {
      const ab = vec3.normalize([], vec3.scale([], vec3.add([], a, b), 0.5))
      const ac = vec3.normalize([], vec3.scale([], vec3.add([], a, c), 0.5))
      const bc = vec3.normalize([], vec3.scale([], vec3.add([], b, c), 0.5))

      divide(a, ab, ac, count - 1)
      divide(ab, b, bc, count - 1)
      divide(bc, c, ac, count - 1)
      divide(ab, bc, ac, count - 1)
    } else {
      tri(a, b, c)
    }
  }

  divide(v1, v12, v6, count)
  divide(v1, v6, v2, count)
  divide(v1, v2, v8, count)
  divide(v1, v8, v11, count)
  divide(v1, v11, v12, count)
  divide(v2, v6, v10, count)
  divide(v6, v12, v5, count)
  divide(v12, v11, v3, count)
  divide(v11, v8, v7, count)
  divide(v8, v2, v9, count)
  divide(v4, v10, v5, count)
  divide(v4, v5, v3, count)
  divide(v4, v3, v7, count)
  divide(v4, v7, v9, count)
  divide(v4, v9, v10, count)
  divide(v5, v10, v6, count)
  divide(v3, v5, v12, count)
  divide(v7, v3, v11, count)
  divide(v9, v7, v8, count)
  divide(v10, v9, v2, count)

  return new Float32Array(points)
}

下图是细分 2 次后的结果。可以发现所有的三角形都一样大。

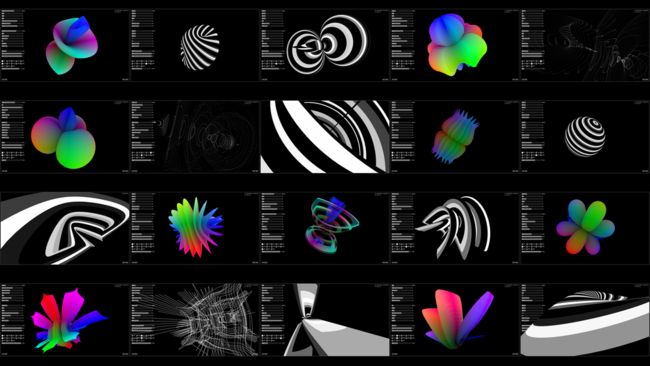
SuperShapes

了解了这么多种方法，其实我们能画的不止球体，只需要在第一种画球方法上做一些修改就可以画出非常多的酷炫的形状！

我们首先要了解 supershape 的公式，打开 这个网站 可以看到这个公式。

把这个公式变成一个函数。

function superShape(theta, m, n1, n2, n3, a = 1, b = 1) {
  return (Math.abs((1 / a) * Math.cos(m * theta / 4)) ** n2 + Math.abs((1 / b) * Math.sin(m * theta / 4)) ** n3) ** (-1 / n1)
}

然后修改一下第一种画球的方法。

function createSuperShape(meridians = 90, parallels = 90) {
  const vertices = [], points = []

  let lat, lon, x, y, z, r1, r2;
  for (let i = 0; i <= parallels; ++i) {
    lat = i * Math.PI / parallels - (Math.PI / 2)
    r2 = superShape(lat, 10, 3, 0.2, 1)
    for (let j = 0; j <= meridians; ++j) {
      lon = j * 2 * Math.PI / meridians - Math.PI
      r1 = superShape(lon, 5.7, 0.5, 1, 2.5)
      x = r1 * Math.cos(lon) * r2 * Math.cos(lat)
      y = r1 * Math.sin(lon) * r2 * Math.cos(lat)
      z = r2 * Math.sin(lat)
      vertices.push([x, y, z])
    }
  }

  function tri(a, b, c) {
    points.push(...vertices[a], ...vertices[b], ...vertices[c])
  }
  function quad(a, b, c, d) {
    tri(a, d, c)
    tri(a, b, d)
  }

  const row = parallels + 1
  let p1, p2
  for (let i = 0; i < parallels; ++i) {
    for (let j = 0; j < meridians; ++j) {
      p1 = i * row + j
      p2 = p1 + row
      quad(p1, p1 + 1, p2, p2 + 1)
    }
  }

  return new Float32Array(points)
}

下图是在 webgl 中渲染的结果。可以通过改变supershape 的参数来得到各种各样的形状，当然也可以在动态的将一个形状过渡到另一个。

总结

这篇文章一共介绍了 4 种画球的方法，每个球体有不同的特点和不同的应用场景，标准球两极的三角形小，靠近赤道的三角形大。正方体细分和正四面体细分的球体，面与面拼接的地方的三角形小。正二十面体细分的球体各个三角形都一样大。

在线预览 https://codesandbox.io/s/sphere-ikqfg 

源码 https://github.com/woopen/sphere

全文完

---

以下文章您可能也会感兴趣：

• 一个 AOP 缓存失效问题的排查

• 小程序开发的几个好的实践

• RabbitMQ 如何保证消息可靠性

• 在 SpringBoot 中使用 STOMP 基于 WebSocket 建立 BS 双向通信

• 聊聊Hystrix 命令执行流程

• SpringFox 源码分析(及 Yapi 问题的另一种解决方案)
  

• Mysql 的字符集以及带来的一点存储影响

我们正在招聘 Java 工程师，欢迎有兴趣的同学投递简历到 [email protected] 。