PSO粒子群算法学习笔记
粒子群算法详解
粒子群算法的迭代公式
-
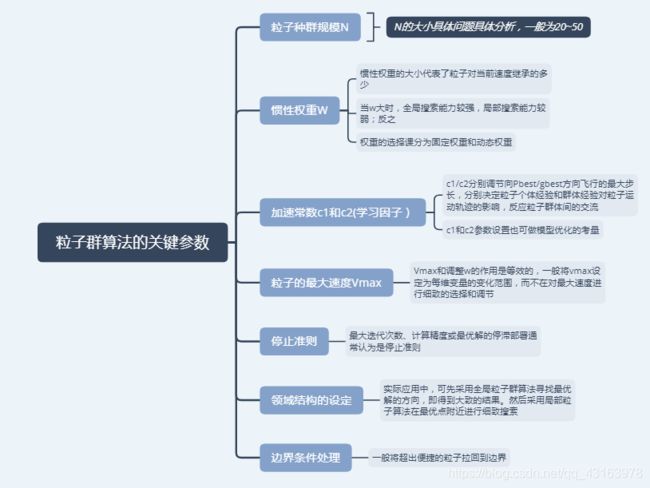
粒子群算法的关键参数
-
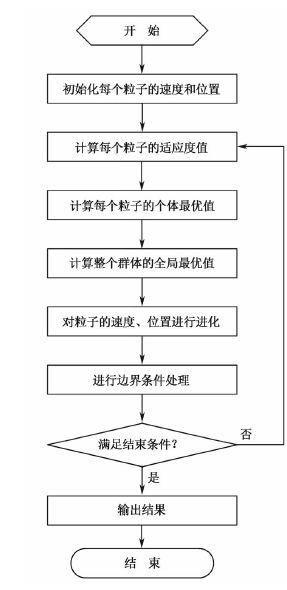
粒子群算法的设计流程
Matlab仿真
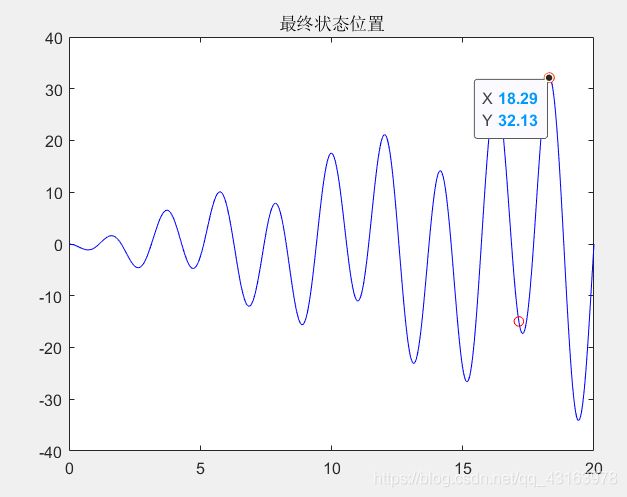
- 求解函数 f=xsin(x)cos(2x)-2xsin(3x) ,求其在区间[0,20]上该函数的最大值。
clc;clear;close all;
%% 初始化种群
f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函数表达式
figure(1);ezplot(f,[0,0.01,20]);
N = 50; % 初始种群个数
d = 1; % 空间维数
ger = 100; % 最大迭代次数
limit = [0, 20]; % 设置位置参数限制
vlimit = [-1, 1]; % 设置速度限制
w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子
for i = 1:d
x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置
end
v = rand(N, d); % 初始种群的速度
xm = x; % 每个个体的历史最佳位置
ym = zeros(1, d); % 种群的历史最佳位置 %zeros(n)生成n阶零矩阵
fxm = zeros(N, 1); % 每个个体的历史最佳适应度
fym = -inf; % 种群历史最佳适应度 %inf代表无穷大
hold on %hode on用于添加新绘图的时候保留当前绘图
plot(xm, f(xm), 'ro');title('初始状态图');
figure(2)%创建一个新窗口
%% 群体更新
iter = 1;
record = zeros(ger, 1); % 记录器
while iter <= ger
fx = f(x) ; % 个体当前适应度
for i = 1:N
if fxm(i) < fx(i)
fxm(i) = fx(i); % 更新个体历史最佳适应度
xm(i,:) = x(i,:); % 更新个体历史最佳位置
end
end
if fym < max(fxm)%max()求函数最大元素
[fym, nmax] = max(fxm); % 更新群体历史最佳适应度
ym = xm(nmax, :); % 更新群体历史最佳位置
end
v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
% 边界速度处理
v(v > vlimit(2)) = vlimit(2);
v(v < vlimit(1)) = vlimit(1);
x = x + v;% 位置更新
% 边界位置处理
x(x > limit(2)) = limit(2);
x(x < limit(1)) = limit(1);
record(iter) = fym;%最大值记录
%%%动态图%%%
% x0 = 0 : 0.01 : 20;
%plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
% pause(0.1)%程序暂停0.1秒后继续执行
iter = iter+1;
end
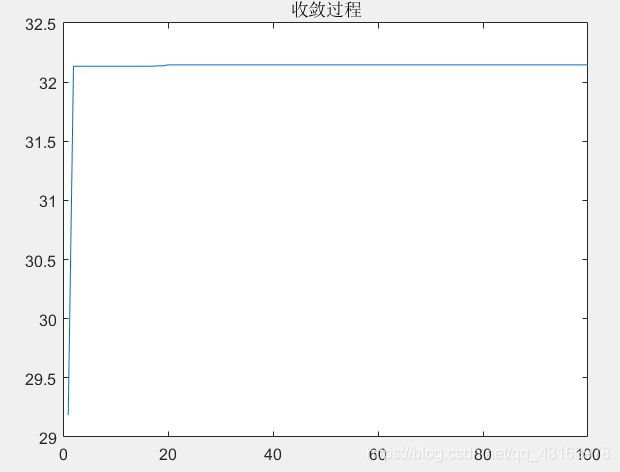
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值:',num2str(fym)]);%disp()函数:显示文本或数组
disp(['变量取值:',num2str(ym)]);
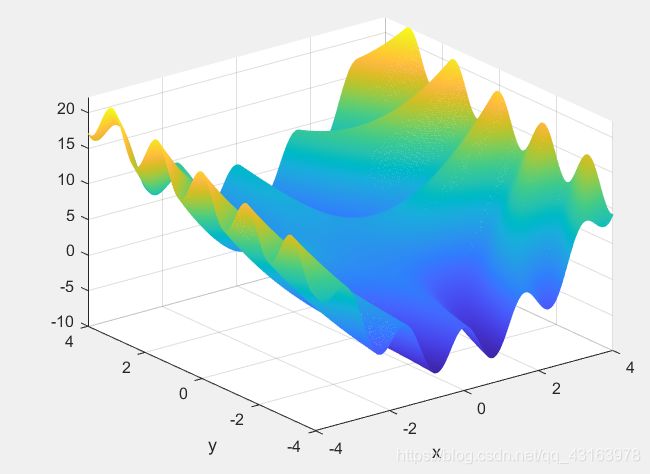
2.求函数f(x,y)=3cos(xy)+x+y*y的最小值,其中x的取值范围为[-4,4],y的取值范围为[-4,4]
x=-4:0.02:4;
y=-4:0.02:4;
N=size(x,2);%size(A,1):获取矩阵A的行数 size(A,2):获取矩阵A的列数
for i=1:N
for j=1:N
z(i,j)=3*cos(x(i)*y(j))+x(i)+y(j)*y(j);
end
end
mesh(x,y,z)%mesh()网格曲面图
xlabel('x')
ylabel('y')
N=100;%群体粒子个数
D=2;%粒子位数
T=200;%最大迭代次数
c1=1.5;%学习因子1
c2=1.5;%学习因子2
Wmax=0.8;%惯性权重最大值
Wmin=0.4;%惯性权重最小值
Xmax=4;%位置最大值
Xmin=-4;%位置最小值
Vmax=1;%速度最大值
Vmin=-1;%速度最小值
%%%初始化种群个体(限定位置和速度)%%%
x=rand(N,D)*(Xmax-Xmin)+Xmin;
v=rand(N,D)*(Vmax-Vmin)+Vmin;
%%%初始化个体最有位置和最优值%%%
p=x;%p为个体最优位置pbest为最优值
pbest=ones(N,1);%ones()生成N*1全1数组
for i=1:N
pbest(i)=func2(x(i,:));
end
%%%初始化全局最有位置和最优值%%%
g=ones(1,D);%g为全局最优位置,gbest为全局最优值
gbest=inf;
for i=1:N
if(pbest(i)<gbest)
g=p(i,:);
gbest=pbest(i);
end
end
gb=ones(1,T);
%%%按照公式一次迭代直到满足精度或者迭代次数%%%
for i=1:T
for j=1:N
%%%%更新个体最优位置和最优解%%%
if(func2(x(j,:))<pbest(j))
p(j,:)=x(j,:);
pbest(j)=func2(x(j,:));
end
%%%更新全局最优位置和最优解%%%
if(pbest(j)<gbest)
g=p(j,:);
gbest=pbest(j);
end
%%%计算动态惯性权重值%%%
w=Wmax-(Wmax-Wmin)*i/T;%shi提出的线性递减权值策略
%%%更新位置和速度值%%%
v(j,:)=w*v(j,:)+c1*rand*(p(j,:)-x(j,:))+c2*rand*(g-x(j,:));
x(j,:)=x(j,:)+v(j,:);
%%%便捷条件处理%%%
for ii=1:D
if (v(j,ii)>Vmax)|(v(j,ii)<Vmin)
v(j,ii)=rand*(Xmax-Xmin)+Xmin;
end
if(x(j,ii)>Xmax)|(x(j,ii)<Xmin)
x(j,ii)=rand*(Xmax-Xmin)+Xmin;
end
end
end
%%%记录历代全局最优解%%%
gb(i)=gbest;
end
g;
gb(end);
figure
plot(gb)
xlabel('迭代次数');
ylabel('适应度值');
title('适应度进化曲线')
%%%适应度函数%%%
function value = func2(x)
value=3*cos(x(1)*x(2))+x(1)+x(2)^2;
end