isodata算法确定k均值聚类的k值

http://baike.baidu.com/view/3167773.htm

http://www.cnblogs.com/huadongw/p/4101422.html

聚类算法：ISODATA算法

1. 与K-均值算法的比较

–K-均值算法通常适合于分类数目已知的聚类，而ISODATA算法则更加灵活；

–从算法角度看， ISODATA算法与K-均值算法相似，聚类中心都是通过样本均值的迭代运算来决定的；

–ISODATA算法加入了一些试探步骤，并且可以结合成人机交互的结构，使其能利用中间结果所取得的经验更好地进行分类。

 

2. ISODATA算法基本步骤和思路

（1）  选择某些初始值。可选不同的参数指标，也可在迭代过程中人为修改，以将N个模式样本按指标分配到各个聚类中心中去。

（2）  计算各类中诸样本的距离指标函数。

（3）~（5）按给定的要求，将前一次获得的聚类集进行分裂和合并处理（（4）为分裂处理，（5）为合并处理），从而获得新的聚类中心。

（6）  重新进行迭代运算，计算各项指标，判断聚类结果是否符合要求。经过多次迭代后，若结果收敛，则运算结束。

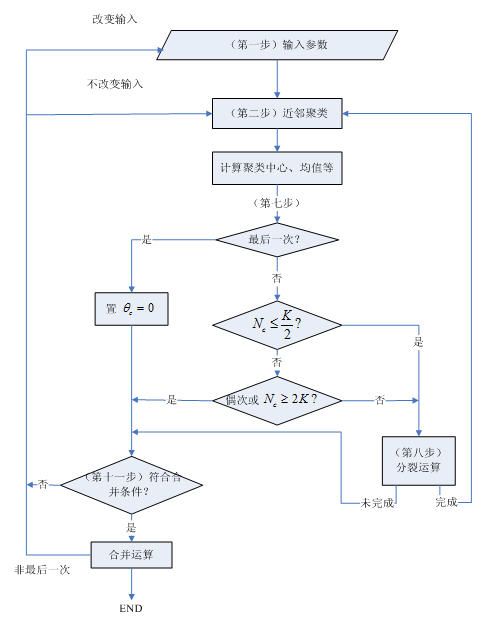
3. ISODATA算法流程图：

4.ISODATA算法

第一步：输入 N 个模式样本 {xi,i=1,2,…,N}

           预选 Nc 个初始聚类中心 {z1,z2,…zNc} ，它可以不等于所要求的聚类中心的数目，其初始位置可以从样本中任意选取。

           预选： K   = 预期的聚类中心数目；

                     θN  = 每一聚类域中最少的样本数目，若少于此数即不作为一个独立的聚类；

                     θS  = 一个聚类域中样本距离分布的标准差；

                     θc = 两个聚类中心间的最小距离，若小于此数，两个聚类需进行合并；

                     L = 在一次迭代运算中可以合并的聚类中心的最多对数；

                     I   = 迭代运算的次数。

第二步：将 N 个模式样本分给最近的聚类 Sj ，假若 Dj=min{∥x−zi∥,i=1,2,⋯Nc}

           ，即 ||x−zj|| 的距离最小，则 x∈Sj 。

第三步：如果 Sj 中的样本数目S_j<θ_N，则取消该样本子集，此时N_c减去1。

           （以上各步对应基本步骤（1））

 

第四步：修正各聚类中心

zj=1Nj∑x∈Sjx,j=1,2,⋯,Nc

第五步：计算各聚类域S_j中模式样本与各聚类中心间的平均距离

D¯j=1Nj∑x∈Sj∥∥x−zj∥∥,j=1,2,⋯,Nc

第六步：计算全部模式样本和其对应聚类中心的总平均距离

D¯=1N∑j=1NNjD¯j

（以上各步对应基本步骤（2））

 

第七步：判别分裂、合并及迭代运算

1. 若迭代运算次数已达到I次，即最后一次迭代，则置θ_c =0，转至第十一步。
2. 若 Nc≤K2
   ，即聚类中心的数目小于或等于规定值的一半，则转至第八步，对已有聚类进行分裂处理。
3. 若迭代运算的次数是偶数次，或 Nc≥2K
   ，不进行分裂处理，转至第十一步；否则（即既不是偶数次迭代，又不满足 Nc≥2K ），转至第八步，进行分裂处理。

（以上对应基本步骤（3））

 

第八步：计算每个聚类中样本距离的标准差向量

σj=(σ1j,σ2j,…,σnj)T

          其中向量的各个分量为

σij=1Nj∑k=1Nj(xik−zij)2−−−−−−−−−−−−−−−⎷

          式中，i = 1, 2, …, n为样本特征向量的维数，j = 1, 2, …, N_c为聚类数，N_j为S_j中的样本个数。

第九步：求每一标准差向量{σ_j, j = 1, 2, …, N_c}中的最大分量，以{σ_jmax, j = 1, 2, …, N_c}代表。

第十步：在任一最大分量集{σ_jmax, j = 1, 2, …, N_c}中，若有σ_jmax>θ_S ，同时又满足如下两个条件之一：

1. D¯j>D¯ 和N_j > 2(θ_N + 1)，即S_j中样本总数超过规定值一倍以上，
2. Nc≤K2

       则将z_j 分裂为两个新的聚类中心和，且N_c加1。 中对应于σ_jmax的分量加上kσ_jmax，其中；中对应于σ_jmax的分量减去kσ_jmax。

       如果本步骤完成了分裂运算，则转至第二步，否则继续。

      （以上对应基本步骤（4）进行分裂处理）

 

第十一步：计算全部聚类中心的距离

                 

Dij=||zi−zj||，i=1,2,…,Nc−1，j=i+1,…,Nc

第十二步：比较D_ij 与θ_c 的值，将D_ij <θ_c 的值按最小距离次序递增排列，即

{Di1j1,Di2j2,…,DiLjL}

             式中 Di1j1<Di2j2<…<DiLjL 。

第十三步：将距离为 Dikjk 的两个聚类中心 Zik 和 Zjk 合并，得新的中心为：

             

z∗k=1Nik+Njk[Nikzik+Njkzjk],k=1,2,⋯,L

              式中，被合并的两个聚类中心向量分别以其聚类域内的样本数加权，使 Z∗k 为真正的平均向量。

             （以上对应基本步骤（5）进行合并处理）

 

第十四步：如果是最后一次迭代运算（即第I次），则算法结束；否则，若需要操作者改变输入参数，转至第一步；若输入参数不变，转至第二步。

              在本步运算中，迭代运算的次数每次应加1。

 [算法结束]

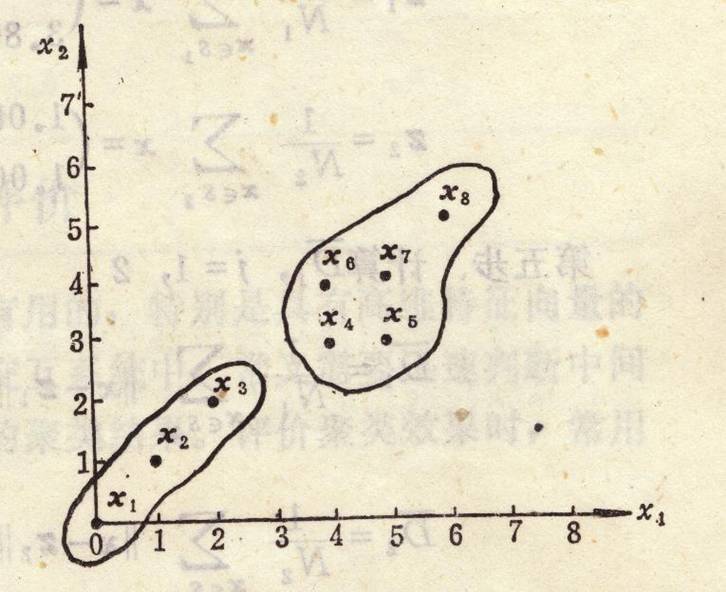
5.例子：试用ISODATA算法对如下模式分布进行聚类分析：

{x1(0,0),x2(3,8),x3(2,2),x4(1,1),x5(5,3),x6(4,8),x7(6,3),x8(5,4),x9(6,4),x10(7,5)}

 

我们可以知道，N=10，n=2。假设取初始值 Nc=1 ，z₁=x₁=(0 0)^T，则运算步骤如下：

（1）   设置控制参数

            取K=3，θ_N=1，θ_S=1，θ_c=4，L=1，I=4

（2）   按最小距离原则将模式集（xi）中每个模式分到某一类中。

          由于此时只有一个聚类中心，因此S₁={x₁, x₂, …, x₁₀}，N₁=10

（3）   因N₁>θ_N ，无子集可抛

（4）   修改聚类中心

z1=1N1∑x∈S1x=(3.93.8)

（5）   计算模式样本与聚类中心间的平均距离 D¯1

D¯1=1N1∑x∈S1∥x−z1∥=3.0749

（6）   计算全部模式样本和其对应聚类中心的总平均距离

D¯=D¯1=3.0749

（7）   因不是最后一次迭代，且 Nc<K/2 ，进入（8）

（8）   计算S₁中的标准差向量

σ1=(2.21132.5219)

（9）  σ1max   中的最大分量是2.5219，因此  σ1max=2.5219 。

（10）因 σ1max>θs  且 Nc<K2 ，可将z₁分裂成两个新的聚          类。设 rj=0.5σ1max≈1.261 .则

z+1=(3.95.061),z−1=(3.92.539)

           为方便起见，将 z+1 和 z−1 表示为z₁和z₂，N_c加1 ， Nc=2 .

（11）   重新进行分类

样本点	特征值		到z1的距离	到z2的距离	聚类结果
X1	0	0	6.3893	4.6537	S2
X2	3	8	3.0737	5.5347	S1
X3	2	2	3.6027	1.975	S2
X4	1	1	4.9902	3.2831	S2
X5	5	3	2.3362	1.1927	S2
X6	4	8	2.9407	5.4619	S1
X7	6	3	2.9424	2.15	S2
X8	5	4	1.5283	1.8288	S1
X9	6	4	2.3528	2.5582	S1
X10	7	5	3.1006	3.9581	S1

S1={x2,x6,x8,x9,x10},N1=5

S2={x1,x3,x4,x5,x7},N2=5

（12）   因N₁>θ_N 且N₂>θ_N，无子集可抛。

（13）   修改聚类中心

z1=1N1∑x∈S1x=(55.8)

z2=1N2∑x∈S2x=(2.81.8)

（14）   计算模式样本与聚类中心间的平均距离 D¯j,j=1,2

D¯1=1N1∑x∈S1∥x−z1∥=2.2806

D¯2=1N2∑x∈S2∥x−z2∥=2.4093

（15）   计算全部模式样本和其对应聚类中心的总平均距离 D¯

D¯=1N∑j=1NNjD¯j=110∑j=12NjD¯j=2.345

（16）   因是偶数次迭代，所以进行合并

（17）   计算聚类对之间的距离

D12=∥z1−z2∥=4.5651

（18）   比较 D12  与θc ， D12 >θc，所以聚类中心不发生合并

（19）   没有达到所需的聚类数，所以继续进行，重新分类

样本点	特征值		到z1的距离	到z2的距离	聚类结果
X1	0	0	7.6577	3.3287	S2
X2	3	8	2.9732	6.2032	S1
X3	2	2	4.8415	0.82462	S2
X4	1	1	6.2482	1.9698	S2
X5	5	3	2.8	2.506	S2
X6	4	8	2.4166	6.3151	S1
X7	6	3	2.9732	3.4176	S1
X8	5	4	1.8	3.1113	S1
X9	6	4	2.0591	3.8833	S1
X10	7	5	2.1541	5.2802	S1

S1={x2,x6,x7,x8,x9,x10},N1=6

S2={x1,x3,x4,x5},N2=4

（20）   因N₁>θ_N 且N₂>θ_N，无子集可抛。

（21）   修改聚类中心

z1=1N1∑x∈S1x=(5.16675.3333)

z2=1N2∑x∈S2x=(21.5)

（22）   计算模式样本与聚类中心间的平均距离， D¯1,j=1,2

D¯1=1N1∑x∈S1∥x−z1∥=2.2673

D¯2=1N2∑x∈S2∥x−z2∥=1.868

（23）   计算全部模式样本和其对应聚类中心的总平均距离 D¯

D¯=1N∑j=1NNjD¯j=110∑j=12NjD¯j=2.1076

（24）   此次是奇数次迭代，并且 Nc>K2 ，所以进行分裂操作

（25）   计算 S1={x2,x6,x7,x8,x9,x10}

和 S21={x1,x3,x4,x5}

的标准差

σ1=(1.34371.972),σ2=(1.87081.118)

（26） σ1max=1.972,σ2max=1.8708

（27）此时， σ1max=1.972>θs,N1=6>2(θN+1)=4 且 D¯1>D¯ ,所以满足分裂的条件，将S1进行分裂。

设 \rj=0.5σ1max≈0.986 ,则

z+1=(5.16676.3193),z−1=(5.16674.3473)

 为方便起见，将 Z+1 和Z_^-表示为 Z11 和 Z12 , Nc 加1， Nc=3 .

（28）重新进行分类

样本点	特征值		到的距离	到的距离	到的距离	聚类结果
X1	0	0	8.1626	6.7523	2.5	S2
X2	3	8	2.7421	4.247	6.5765	S11
X3	2	2	5.3558	3.9418	0.5	S2
X4	1	1	6.7569	5.3447	1.118	S2
X5	5	3	3.3235	1.3576	3.3541	S12
X6	4	8	2.046	3.8345	6.8007	S11
X7	6	3	3.4223	1.5842	4.272	S12
X8	5	4	2.3253	0.38524	3.9051	S12
X9	6	4	2.4645	0.90278	4.717	S12
X10	7	5	2.2587	1.946	6.1033	S12

S11={x2,x6},N11=2

S12={x5,x7,x8,x9,10},N12=5

（29）   因N₁₁>θ_N 且N₁₂>θ_N且N₂>θ_N，无子集可抛

（30）   修改聚类中心

S2={x1,x3,x4},N2=3

z11=1N11∑x∈S11x=(3.58)

z12=1N12∑x∈S12x=(5.83.8)

z2=1N2∑x∈S2x=(11)

（31）   计算模式样本与聚类中心间的平均距离 D¯j

D¯11=1N11∑x∈S11∥x−z11∥=0.5

D¯12=1N12∑x∈S12∥x−z12∥=0.9521

D¯2=1N2∑x∈S2∥x−z2∥=0.94281

（32）   计算全部模式样本和其对应聚类中心的总平均距离 D¯

D¯=1N∑NjD¯j=110∑NjD¯j=0.85889

（33）   因是偶数次迭代，所以进行合并

（34）   计算聚类对之间的距离

	Z11	Z12	Z13
Z11	0	4.7885	7.433
Z12	4.7885	0	5.557
Z2	7.433	5.557	0

所以

D1112=∥z11−z12∥=4.7885>θc=4

D112=∥z11−z2∥=7.433>θc=4

D122=∥z12−z2∥=5.557>θc=4

            故没有可以合并的类

（35）   最后一次迭代，算法结束。

             最终的聚类结果是

S1={x2,x6},S2={x5,x7,x8,x9,x10},S3={x1,x3,x4},N2=3

6 .聚类结果的评价

     迅速评价聚类结果，在上述迭代运算中是很重要的，特别是具有高维特征向量的模式，不能直接看清聚类效果，因此，可考虑用以下几个指标来评价聚类效果：

    –聚类中心之间的距离

          •距离值大，通常可考虑分为不同类

    –聚类域中的样本数目

          •样本数目少且聚类中心距离远，可考虑是否为噪声

    –聚类域内样本的距离方差

          •方差过大的样本可考虑是否属于这一类

 

     模式聚类目前还没有一种通用的放之四海而皆准的准则，往往需要根据实际应用来选择合适的方法。

 

该资料整理于国科大《模式识别》讲稿和作业。