matlab中的delaunay,使用 Delaunay 三角剖分
使用 delaunayTriangulation 类
delaunayTriangulation 类提供另一种在 MATLAB 中创建 Delaunay 三角剖分的方法。虽然 delaunay 和 delaunayTriangulation 使用相同的基本算法并生成相同的三角剖分,但 delaunayTriangulation 提供了适用于开发基于 Delaunay 的算法的补充方法。这些方法与函数类似,可以将它们与三角剖分数据一起打包到称为类的容器中。将所有内容集中在类中,这样可以提供更加有条理的结构,从而提高易用性。它还可以提高基于三角剖分的搜索的性能,例如点位置和最近邻位置。delaunayTriangulation 支持对 Delaunay 三角剖分进行增量编辑。还可以实行二维中的边约束。
三角剖分表示法引入了 triangulation 类,该类支持对二维和三维三角剖分进行拓扑和几何查询。delaunayTriangulation 是一种特殊的 triangulation。这意味着除了可以对 delaunayTriangulation 执行 Delaunay 特定的查询外,还可以执行任何 triangulation 查询。在比较正式的 MATLAB 语言术语中,delaunayTriangulation 是 triangulation 的子类。
此示例说明如何使用 delaunayTriangulation 创建、查询和编辑 seamount 数据的 Delaunay 三角剖分。海底山数据集包含用于定义海拔山曲面的 (x, y) 位置和对应的海拔 (z)。
加载 (x, y) 数据并进行三角剖分。
load seamount
DT = delaunayTriangulation(x,y)
DT =
delaunayTriangulation with properties:
Points: [294x2 double]
ConnectivityList: [566x3 double]
Constraints: []
由于没有施加任何边约束,因此 Constraints 属性为空。Points 属性表示顶点坐标,ConnectivityList 属性表示三角形。这两个属性共同定义了三角剖分的矩阵数据。
delaunayTriangulation 类是矩阵数据的封装类,并且提供了一组补充方法。可以按照访问结构体字段的方式访问 delaunayTriangulation 中的属性。
访问顶点数据。
DT.Points;
访问连接数据。
DT.ConnectivityList;
访问 ConnectivityList 属性中的第一个三角形。
DT.ConnectivityList(1,:)
ans = 1×3
205 230 262
delaunayTriangulation 提供了一种对 ConnectivityList 属性矩阵进行索引的简单方法。
访问第一个三角形。
DT(1,:)
ans = 1×3
205 230 262
检查第一个三角形的第一个顶点。
DT(1,1)
ans = 205
检查三角剖分中的所有三角形。
DT(:,:);
对 delaunayTriangulation 输出 DT 进行索引,这与对 delaunay 的三角剖分数组输出进行索引类似。二者的区别是您可以对 DT 调用额外方法(例如 nearestNeighbor 和 pointLocation)。
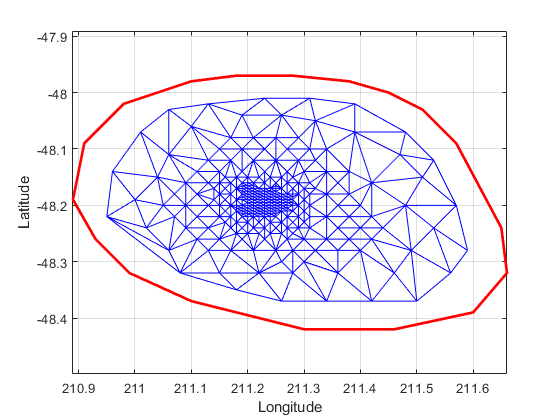
使用 triplot 绘制 delaunayTriangulation。triplot 函数不是 delaunayTriangulation 方法,但它接受并可绘制 delaunayTriangulation。
triplot(DT);
axis equal
xlabel('Longitude'), ylabel('Latitude')
grid on
或者,可以使用 triplot(DT(:,:), DT.Points(:,1), DT.Points(:,2)); 获取相同的绘图。
使用 delaunayTriangulation 方法 convexHull 计算凸包并将其添加到绘图。由于您已经有一个 Delaunay 三角剖分,因此可利用此方法来获得凸包,效率比使用 convhull 的完全计算方法更高。
hold on
k = convexHull(DT);
xHull = DT.Points(k,1);
yHull = DT.Points(k,2);
plot(xHull,yHull,'r','LineWidth',2);
hold off
您可以按增量方式编辑 delaunayTriangulation,以添加或删除点。如果需要将点添加到现有的三角剖分,增量添加方法的速度要快于对增广点集进行完整的重新三角剖分。当要删除的点数量相对现有的点数量较小时,增量点删除的效率更高。
编辑三角剖分,删除上一次计算的凸包上的点。
figure
plot(xHull,yHull,'r','LineWidth',2);
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
% The convex hull topology duplicates the start and end vertex.
% Remove the duplicate entry.
k(end) = [];
% Now remove the points on the convex hull.
DT.Points(k,:) = []
DT =
delaunayTriangulation with properties:
Points: [274x2 double]
ConnectivityList: [528x3 double]
Constraints: []
% Plot the new triangulation.
hold on
triplot(DT);
hold off
紧靠凸包边界内侧有一个未删除的顶点。在图窗中使用放大工具可以看到,它确实处于凸包以内。您可以绘制顶点标签,以确定此顶点的索引,并从三角剖分中将其删除。或者,可以使用 nearestNeighbor 方法更轻松地确定索引。
该点靠近位置 (211.6, -48.15)。使用 nearestNeighbor 方法求最近的顶点。
vertexId = nearestNeighbor(DT, 211.6, -48.15)
vertexId = 50
现在从三角剖分中删除该顶点。
DT.Points(vertexId,:) = []
DT =
delaunayTriangulation with properties:
Points: [273x2 double]
ConnectivityList: [525x3 double]
Constraints: []
对新的三角剖分进行绘图。
figure
plot(xHull,yHull,'r','LineWidth',2);
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
hold on
triplot(DT);
hold off
将点添加到现有的三角剖分。添加 4 个点,在三角剖分的周围构成一个矩形。
Padditional = [210.9 -48.5; 211.6 -48.5; ...
211.6 -47.9; 210.9 -47.9];
DT.Points(end+(1:4),:) = Padditional
DT =
delaunayTriangulation with properties:
Points: [277x2 double]
ConnectivityList: [548x3 double]
Constraints: []
关闭所有现有图窗。
close all
对新的三角剖分进行绘图。
figure
plot(xHull,yHull,'r','LineWidth',2);
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
hold on
triplot(DT);
hold off
您可以编辑三角剖分中的点,将其移到新位置。编辑附加点集的第一个点(顶点 ID 274)。
DT.Points(274,:) = [211 -48.4];
关闭所有现有图窗。
close all
对新的三角剖分进行绘图
figure
plot(xHull,yHull,'r','LineWidth',2);
axis equal
xlabel('Longitude'),ylabel('Latitude')
grid on
hold on
triplot(DT);
hold off
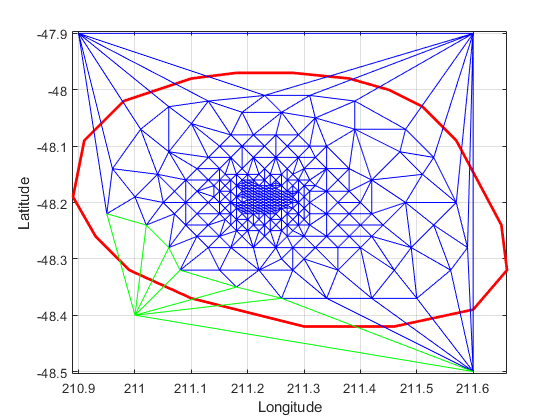
使用 triangulation 类的方法 vertexAttachments 求连接的三角形。由于连接到顶点的三角形数量是可变的,因此该方法将在元胞数组中返回连接的三角形 ID。您需要使用括号提取内容。
attTris = vertexAttachments(DT,274);
hold on
triplot(DT(attTris{:},:),DT.Points(:,1),DT.Points(:,2),'g')
hold off
delaunayTriangulation 也可以用于对三维空间中的点进行三角剖分。生成的三角剖分由四面体构成。
此示例说明如何使用 delaunayTriangulation 创建并绘制三维点的三角剖分。
rng('default')
P = rand(30,3);
DT = delaunayTriangulation(P)
DT =
delaunayTriangulation with properties:
Points: [30x3 double]
ConnectivityList: [102x4 double]
Constraints: []
faceColor = [0.6875 0.8750 0.8984];
tetramesh(DT,'FaceColor', faceColor,'FaceAlpha',0.3);
tetramesh 函数会同时绘制三角剖分的内面和外面。对于大型三维三角剖分,绘制内面可能导致不必要的资源使用。绘制边界可能更加适宜。您可以使用 freeBoundary 方法获取矩阵格式的边界三角剖分。然后将结果传递给 trimesh 或 trisurf。