对比学习论文综述
目录
- 第一阶段:百花齐放
-
- InstDisc (InstDisc + Memory bank)
- InvaSpread (InstDisc + End-to-end)
- Contrastive Predictive Coding (CPC)
- Contrastive Multiview Coding (CMC)
- 第二阶段:CV 双雄
-
- MoCov1 (Momentum Contrast)
- SimCLRv1 (Simple Contrastive Learning)
- MoCov2
- SimCLRv2
- SWAV (SWAp Assignment Views)
- 第三阶段:不用负样本
-
- BYOL (Bootstrap Your Own Latent)
- 针对 BYOL 的博客和他们的回应
- SimSiam (Simple Siamese)
- 第四阶段:基于 Transformer
-
- MoCov3
- DINO (self-DIstillation with NO labels)
- References
第一阶段:百花齐放
InstDisc (InstDisc + Memory bank)
- paper: Unsupervised Feature Learning via Non-Parametric Instance Discrimination
Motivation
- 作者提出的 Instance Discrimination 其实是受到了有监督学习的启发。如下图所示,给模型一张 leopard 的图片,logits 较高的类别都是与 leopard 在视觉上非常相近的类别 (e.g. jaguar and cheetah),是数据本身显然的相似性而非语义标签让模型觉得这些类别如此相近。由此可见,一个典型的判别式学习方法能够自动地发掘出类别间的相似性而不需要被显式地指导,换言之,类别间的相似性是通过视觉数据本身而非语义标签学得的 (class-wise supervision 能够捕捉到类别间的相似性)

- 受到上述启发,Instance Discrimination (个体判别) 将 class-wise supervision 推广到了 instance-wise supervision,将每一个样本都看作一个单独的类别,让模型学得的特征能够区分出这些个体实例,这样最终学得的特征就能捕捉到样本间的相似性。具体而言,就是从数据集中随机选取一张图片 x i x_i xi,对该图片做随机裁剪并进行数据增强 (random color jittering, random horizontal flip, and random grayscale conversion) 得到 x i 1 x_i^1 xi1 和 x i 2 x_i^2 xi2。由于它们都是从同一张图片得到的,语义信息应该相近,因此可以将 x i 1 x_i^1 xi1 视为锚点, x i 2 x_i^2 xi2 视为正样本,数据集中的所有其他样本都是不相似的负样本,这就相当于将数据集中的每一个样本都看作一个单独的类别。在得到正样本和负样本之后,利用 对比损失 (contrastive loss) 函数 (e.g. NCE, InfoNCE) 使得相似样本的特征尽量接近,不相似样本的特征尽量远离即可
Approach
- Memory Bank: 由于数据集中样本数量很多,为了减少计算量,InstDisc 使用了 memory bank 用于存储数据集中所有样本的特征 (这就要求每个特征的维度不能太大,否则存储代价就太大了,因此 InstDisc 选择的特征维数为 128)。前向过程如下:假如 batch size 为 256,那么就可以生成 256 个锚点和 256 个对应的正样本,对于每个锚点,再从 memory bank 里采样出 4096 个负样本,有了正样本和负样本,就可以计算 NCE loss 去更新模型参数。更新完网络后,为了保证 memory bank 里的特征不太过时,还需要把本次 mini-batch 里样本对应的特征存入 memory bank 更新掉旧值
- Proximal Regularization: InstDisc 利用 Proximal Regularization 来让 memory bank 中的特征进行动量更新,进而保证 memory bank 中特征的一致性
InvaSpread (InstDisc + End-to-end)
- paper: Unsupervised Embedding Learning via Invariant and Spreading Instance Feature
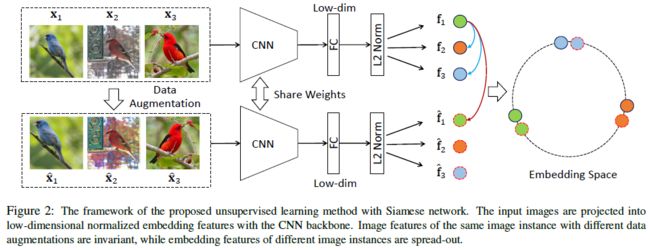
- InvaSpread 可以看作 SimCLR 的前作,它使用 Instance discrimination 这个代理任务,主要思想就是相同实例的特征应该尽量保持不变 (Invariant),而不同实例的特征应该尽量分开 (Spreading)。它可以被理解为 SimCLR 的前身,没有使用额外的数据结构去存储大量的负样本,正负样本就是来自于同一个 mini-batch,而且只使用一个编码器进行端到端的学习

Proposed Method
- 前向过程 (end-to-end):假如 batch size 为 256,那么就有 256 张输入图片,经过数据增强后又得到 256 张图片。对于 x 1 x_1 x1 而言, x ^ 1 \hat x_1 x^1 就是它的正样本,其余 ( 256 − 1 ) × 2 = 510 (256-1)\times2=510 (256−1)×2=510 张图片就是负样本,计算 NCE loss 后就可以更新网络参数了
(通过在一个 mini-batch 中选取正负样本,InvaSpread 可以使用一个编码器进行端到端的训练)
在 InvaSpread 中,负样本的个数受限于 batch size,作者也没有 TPU 只选取了 256 作为 batch size,最终限制了模型的性能
Contrastive Predictive Coding (CPC)
- paper: Representation Learning with Contrastive Predictive Coding
- CPC 没有采用个体判别作为代理任务,而是定义了一个生成式的代理任务,它形成了一个通用的结构,能用相同的步骤处理音频、文字、图片 (将图片看作 patch 序列),还可以在强化学习中使用。这里为了简单起见,使用一个音频信号作为输入。它的基本想法是,假设有一个时序序列,我们将之前时刻的输入 x t − 3 , . . . , x t x_{t-3},...,x_t xt−3,...,xt 都喂给一个编码器 g e n c g_{enc} genc,编码器会返回相应的特征 z t − 3 , . . . , z t z_{t-3},...,z_t zt−3,...,zt,接着把这些特征再喂给一个自回归模型 g a r g_{ar} gar (e.g. RNN, LSTM) 得到 context representation c t c_t ct。如果这个上下文的特征表示足够好,那它应该可以预测未来时刻的特征输出,也就是 c t c_t ct 会与 z t + 1 , . . . z t + 4 z_{t+1},...z_{t+4} zt+1,...zt+4 比较接近,因此就可以将真实的未来时刻的特征输出作为正样本。而负样本的定义就比较广泛了,可以取任意输入经过编码器编码后作为负样本

Contrastive Multiview Coding (CMC)
- paper: Contrastive Multiview Coding
- 人类可以通过多个感官去感知世界,对于一个场景而言,每个感官得到的信息都是不完整且带有噪声的,但一些重要信息却可以在不同感官视角下共享 (e.g., a “dog” can be seen, heard, and felt),因此,一个强大的特征表示具有 view-invariant 的特性,能够抓住所有视角下的重要信息。为此 CMC 提出了一个 新的代理任务 (多视角的对比学习) 用于最大化不同感官视角之间的互信息,使得模型学得的特征满足 view-invariant
- CMC 选择了 NYU RGBD 数据集,这个数据集下每张图片都有 4 个不同的视角 (i.e. 原始图像,图像对应的深度信息,Surface normal 和 物体分割图像),CMC 将这 4 张图片对应的特征作为正样本 (正样本来自于多个视角),其余图片对应的特征均为负样本。同时,由于不同视角/模态的输入分布可能大不相同,因此在处理不同视角/模态时就需要使用不同的编码器,这可能会导致编码器的数量与视角/模态的数量一致,增加了训练成本

CMC 是较早探索多视角对比学习的工作,它不仅证明了对比学习的灵活性,还证明了多模态、多视角的可行性。CMC 的原班人马甚至在这之后还做了一篇模型蒸馏的工作,将 Student 和 Teacher 模型的输出作为一个正样本对进行对比学习。OpenAI 在这之后也很快推出了 CLIP,将图片和描述它的文本当作正样本对来进行多模态的对比学习
第二阶段:CV 双雄
MoCov1 (Momentum Contrast)
- paper: Momentum Contrast for Unsupervised Visual Representation Learning
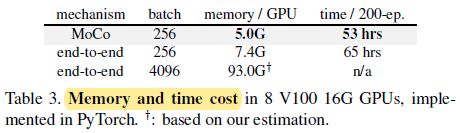
A big and consistent dictionary
详见 MoCo 论文逐段精读【论文精读】
SimCLRv1 (Simple Contrastive Learning)
- paper: A Simple Framework for Contrastive Learning of Visual Representations
SimCLR
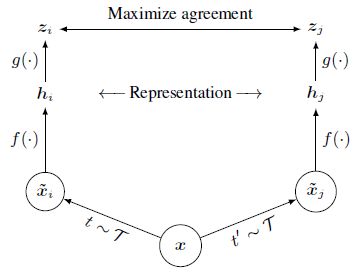
- SimCLR 的思路与 InvaSpread 类似,使用个体判别的代理任务,正负样本来自于同一个 mini-batch,只使用一个编码器进行端到端的学习。具体来说,对于 mini-batch 中的一个样本 x x x,先利用数据增强得到 x ^ i \hat x_i x^i 和 x ^ j \hat x_j x^j,然后利用编码器 f f f 得到编码特征 h i h_i hi 和 h j h_j hj。与 InvaSpread 不同的是,SimCLR 新增了 projection head g g g,通过 g g g 得到 z i z_i zi 和 z j z_j zj,然后利用对比损失使得正样本对应的 z z z 尽量接近,负样本对应的 z z z 尽量远离,损失函数采用 normalized temperature scaled 的交叉熵函数 (normalized 指在 z z z 之后进行了 L2 归一化,temperature scaled 指在交叉熵函数中加入了温度系数 τ \tau τ)
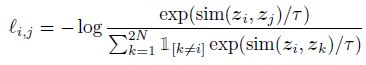
- 相比 InvaSpread,SimCLR (1) 新增了 projection head g g g,projection head 只在训练时使用,微调时使用 encoder 得到的特征 h h h 即可 ( g g g 其实就是 FC + ReLU,但却能让模型最后在 ImageNet 分类任务上提升将近 10 个点之多) 为什么 projection head 带来的提升这么大? 作者也给出了解释: A nonlinear projection head improves the
representation quality of the layer before it. 当使用 projection head 时, z = g ( h ) z=g(h) z=g(h) 会对数据增强不敏感,也就是说可能会损失颜色、物体方位等对下游任务比较重要的信息。通过非线性变换 g g g,模型就能在 h h h 里更多地保留这类信息,从而提升下游任务的性能
 (2) 使用了更多的数据增强操作 (论文发现数据增强操作对无监督的对比学习很重要)
(2) 使用了更多的数据增强操作 (论文发现数据增强操作对无监督的对比学习很重要) (3) 使用了更大的 batch size 并且训练了更久
(3) 使用了更大的 batch size 并且训练了更久
ImageNet Top-1 accuracy
SimCLR 的负样本采样个数受限于 batch size,作者团队有 “钞能力” 把 batch size 加到很大才会有如此好的效果
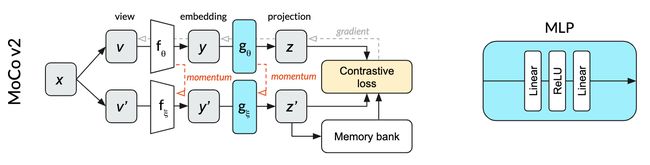
MoCov2
- paper: Improved Baselines with Momentum Contrastive Learning
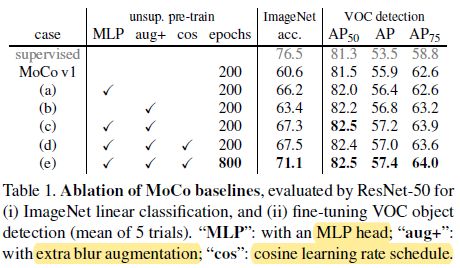
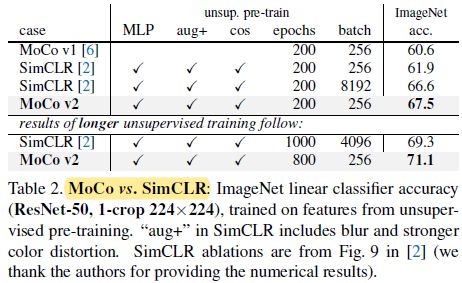
- MoCov2 主要是将 SimCLR 中的一些技术融合到了 MoCo 中,包括 MLP projection head,更多的数据增强操作 和 训练更长时间,最终取得了优于 SimCLR 的结果
SimCLRv2
- paper: Big Self-Supervised Models are Strong Semi-Supervised Learners
- 这篇工作主要讲了如何用 SimCLRv2 去做半监督学习,但下面我们主要介绍 SimCLRv2 相对于 SimCLRv1 的改进:
- (1) 使用了更大的 152-layer ResNet with 3× wider channels and selective kernels (SK) (SK 是一种通道层面的注意力机制,可以提升网络的 parameter efficiency)
- (2) 使用了更深的 projection head (由一层 MLP 变成了两层 MLP)
- (3) 使用了 MoCo 的队列字典和动量编码器。但由于原来的 SimCLR 已经使用了很大的 batch size,这一点的改进并不是特别大
SWAV (SWAp Assignment Views)
- paper: Unsupervised Learning of Visual Features by Contrasting Cluster Assignments
SWAV Method overview
- 基于个体判别的对比学习将数据集中的每个样本都看作单独的一类 (计算损失时使用 one-hot label),直接使用网络抽取的特征 z z z 进行对比学习,但即使像 MoCo 一样取 60000 个负样本进行对比学习也仍然只是一个近似,并且采样的负样本可能类别不均衡,有的甚至是正样本,会给模型学习带来困难。而 SWAV 则认为没必要跟所有的负样本进行对比,可以利用聚类的思想找到 K K K 个聚类中心来代表整个数据集,然后由聚类中心来为每个样本生成低维的软标签 (i.e. Codes),最后利用 “swapped’’ prediction 进行对比学习
Compared to SimCLR, SWAV pretraining converges faster and is less sensitive to the batch size. Moreover, SWAV is not that sensitive to the number of clusters. Typically 3K clusters are used for ImageNet. In general, it is recommended to use approximately one order of magnitude larger than the real class labels. For STL10 which has 10 classes, 512 clusters would be enough.
Definitions
- Prototypes / Clusters: K K K 个 单位长度的 D D D- d d d 聚类中心 c 1 , . . . , c K c_1,...,c_K c1,...,cK,用一个 D × K D\times K D×K 的矩阵 C C C 表示。 K K K 个聚类中心均由卷积网络反向传播训练得到,随着数据集中常见的特征而变化,可以看作是整个数据集的一个低维投影
- Codes / Assignments: Codes 是通过迭代生成的,可以看作是由聚类得到的每个样本的软标签 (ground-truth),用一个 K × B K\times B K×B 的矩阵 Q Q Q 表示 (现在暂时不讲如何计算,将它看作样本的软标签即可)
- Swapped Prediction: 对于两个正样本特征 z 1 z_1 z1 和 z 2 z_2 z2,它们包含有相似的信息,因此它们的软标签 Codes 也是相似的。因此我们就可以用其中一个特征和 Prototypes 来预测另一个特征的 Codes (通过与聚类中心内积得到预测的软标签)
SWAV method Steps
- (1) 由输入图像 X X X 通过随机的数据增强得到 N N N 个 views,再由 CNN 得到相应的 N N N 个特征 Z Z Z。计算所有特征 Z Z Z ( D × N D\times N D×N) 和所有聚类中心 C C C ( D × K D\times K D×K) 之间的相似度 (i.e. s o f t m a x ( C T Z , d i m = 0 ) softmax(C^TZ,dim=0) softmax(CTZ,dim=0)),也就是 Swapped Prediction 中每个 view 得到的预测值。迭代地计算 Codes Q Q Q ( K × N K\times N K×N),也就是 Swapped Prediction 中每个 view 的 ground-truth
- (2) 对于 N N N 个 views,利用 Swapped Prediction 两两计算 cross entropy loss。对于两个 views z s z_s zs 和 z t t z_tt ztt,Codes 为 q s , q t q_s,q_t qs,qt,预测值为 p s , p t p_s,p_t ps,pt,Swapped Prediction Loss 为
L ( z t , z s ) = ℓ ( z t , q s ) + ℓ ( z s , q t ) L\left(\mathbf{z}_{t}, \mathbf{z}_{s}\right)=\ell\left(\mathbf{z}_{t}, \mathbf{q}_{s}\right)+\ell\left(\mathbf{z}_{s}, \mathbf{q}_{t}\right) L(zt,zs)=ℓ(zt,qs)+ℓ(zs,qt)其中,
ℓ ( z t , q s ) = − ∑ k q s ( k ) log p t ( k ) , where p t ( k ) = exp ( 1 τ z t ⊤ c k ) ∑ k ′ exp ( 1 τ z t ⊤ c k ′ ) and τ is a temperature parameter \begin{aligned}\ell\left(\mathbf{z}_{t}, \mathbf{q}_{s}\right)&=-\sum_{k} \mathbf{q}_{s}^{(k)} \log \mathbf{p}_{t}^{(k)},\\\quad \text { where } \quad &\mathbf{p}_{t}^{(k)}=\frac{\exp \left(\frac{1}{\tau} \mathbf{z}_{t}^{\top} \mathbf{c}_{k}\right)}{\sum_{k^{\prime}} \exp \left(\frac{1}{\tau} \mathbf{z}_{t}^{\top} \mathbf{c}_{k^{\prime}}\right)}\quad \text{and}\\&\tau\text{ is a temperature parameter} \end{aligned} ℓ(zt,qs) where =−k∑qs(k)logpt(k),pt(k)=∑k′exp(τ1zt⊤ck′)exp(τ1zt⊤ck)andτ is a temperature parameter
Digging into SWAV’s math: approximating Q Q Q
- An Optimal Transport Problem with Entropic Constraint: 在 SWAV 中,code vectors 是在每个迭代中被在线计算的 (online 表示在每个迭代中动态地估计 Q Q Q) 而非使用梯度下降。设有 K K K 个聚类中心,batch size 为 B B B,SWAV 将最优的 code matrix Q = [ q 1 , . . . , q B ] ∈ R K × B Q=[q_1,...,q_B]\in R^{K\times B} Q=[q1,...,qB]∈RK×B 视为带有熵约束的最优传输问题的解,可以定义为如下形式:
Q ∗ = max Q ∈ Q Tr ( Q T C T Z ) + ε H ( Q ) Q = { Q ∈ R + K × B ∣ Q 1 B = 1 K 1 K , Q T 1 K = 1 B 1 B } \begin{gathered} \mathbf{Q}^{*}=\max _{\mathbf{Q} \in \mathcal{Q}} \operatorname{Tr}\left(\mathbf{Q}^{T} \mathbf{C}^{T} \mathbf{Z}\right)+\varepsilon H(\mathbf{Q}) \\ \mathcal{Q}=\left\{\mathbf{Q} \in \mathbb{R}_{+}^{K \times B} \mid \mathbf{Q} \mathbf{1}_{B}=\frac{1}{K} \mathbf{1}_{K}, \mathbf{Q}^{T} \mathbf{1}_{K}=\frac{1}{B} \mathbf{1}_{B}\right\} \end{gathered} Q∗=Q∈QmaxTr(QTCTZ)+εH(Q)Q={Q∈R+K×B∣Q1B=K11K,QT1K=B11B}其中 H ( Q ) = − ∑ i j Q i j log Q i j H(\mathbf{Q})=-\sum_{i j} \mathbf{Q}_{i j} \log \mathbf{Q}_{i j} H(Q)=−∑ijQijlogQij 为矩阵的熵,超参数 ε \varepsilon ε 用于控制熵正则化的强度。集合 Q \mathcal{Q} Q 要求 Q Q Q 满足 (1) 所有元素为正;(2) 每行的和为 1 / K 1/K 1/K;(3) 每列的和为 1 / B 1/B 1/B (上述三个要求隐式地规定了所有元素的和为 1,因此可以对 Q Q Q 从概率的角度进行解释。例如一个最简单的满足要求的矩阵每个元素均为 1 / ( B K ) 1/(BK) 1/(BK),它表示每个样本属于各个聚类中心的概率相同,也就是服从均匀分布)- Optimal transport without entropy: 首先我们来看上述优化问题的第一项
Q ∗ = max Q ∈ Q Tr ( Q T C T Z ) \mathbf{Q}^{*}=\max _{\mathbf{Q} \in \mathcal{Q}} \operatorname{Tr}\left(\mathbf{Q}^{T} \mathbf{C}^{T} \mathbf{Z}\right) Q∗=Q∈QmaxTr(QTCTZ)由于 C C C ( D × K D\times K D×K) 和 Z Z Z ( D × B D\times B D×B) 中的向量均为单位向量,矩阵乘积 C T Z C^TZ CTZ ( K × B K\times B K×B) 就计算了所有样本和聚类中心之间的相似度,第 i i i 列即为样本 i i i 与所有聚类中心的相似度。因此, Q T C T Z Q^TC^TZ QTCTZ ( B × B B\times B B×B) 的迹就可以看作是所有样本与各个聚类中心相似度的加权和。因此直观来看, Q Q Q 的最优解会给跟高相似度的项分配更大的权重 (assign large weights to larger similarity scores),但这样必然会导致生成的软标签 Q Q Q 更加偏向于 one-hot vector,只给最相似的类别高分,其余都给低分,这就会使得模型更容易产生 mode collapse (i.e. 所有样本都被始终分配到同一个聚类中心上)
(现在重新看 Q Q Q 的限制,行和列加和的限制其实就是分别在要求每个聚类中心和每个样本的总权重相同。行上的限制有利于更好地让聚类中心代表数据集 (summarize the dataset) (各个样本有相同的概率属于每个聚类中心)) - The entropy constraint: 熵约束项可以让我们控制软标签 Q Q Q 的平滑程度 (smoothness)。当 ε → ∞ \varepsilon\rightarrow\infty ε→∞ 时,最优解 Q ∗ Q^* Q∗ 就是一个熵最大的矩阵,每个元素均为 1 / ( B K ) 1/(BK) 1/(BK),所有样本都被均匀分配给了所有聚类中心
- Optimal transport without entropy: 首先我们来看上述优化问题的第一项
- Online estimation of Q ∗ Q^* Q∗ for SWAV: 上述问题的近似解可以用 Sinkhorn-Knopp 算法迭代得到。从该算法 paper 第 5 面的公式 2 可知,解为如下形式:
Q ∗ = Diag ( u ) exp ( C T Z ε ) Diag ( v ) \mathbf{Q}^{*}=\operatorname{Diag}(\mathbf{u}) \exp \left(\frac{\mathbf{C}^{T} \mathbf{Z}}{\varepsilon}\right) \operatorname{Diag}(\mathbf{v}) Q∗=Diag(u)exp(εCTZ)Diag(v)其中, u u u 和 v v v 分别为列和行的归一化向量。想要算出精准解是不高效的,因此 Sinkhorn-Knopp 算法提供了一种快速的迭代算法:(1) 用 exp ( C T Z ε ) \exp \left(\frac{\mathbf{C}^{T} \mathbf{Z}}{\varepsilon}\right) exp(εCTZ) 对 Q Q Q 进行初始化,然后交替对矩阵 Q Q Q 进行行归一化和列归一化,伪代码如下:
# Sinkhorn-Knopp
def sinkhorn(scores, eps=0.05, niters=3):
Q = exp(scores / eps).T
Q /= sum(Q)
K, B = Q.shape
r, c = ones(K) / K, ones(B) / B
for _ in range(niters):
Q *= (r / sum(Q, dim=1)).unsqueeze(1) # row norm
Q *= (c / sum(Q, dim=0)).unsqueeze(0) # column norm
return (Q / sum(Q, dim=0, keepdim=True)).T
The multi-crop idea: augmenting views with smaller images
- 除了使用聚类中心生成软标签来进行对比学习之外,SWAV 使用的另一个重要 trick 就是 multi-crop。之前的对比学习工作对一个样本大都只使用两个大 crops 去生成两个重叠区域很大的 views (e.g. 在 256 × 256 256\times256 256×256 的图片上随机 crop 两个 224 × 224 224\times224 224×224 的图片),但这样的大 crop 抓住的是图片的全局特征而无法让模型学到图片的局部特征。为了让模型更好地捕捉到局部特征,SWAV 是随机裁剪并 resize 了 2 global (i.e. 224 × 224 224\times224 224×224) views 和 V V V local (i.e. 96 × 96 96\times96 96×96) views (Typically, V = 4 V=4 V=4) 来进行对比学习,其中的 local views 就可以很好地捕捉图片的局部特征,同时较小的分辨率也不会过度增加内存和计算负荷
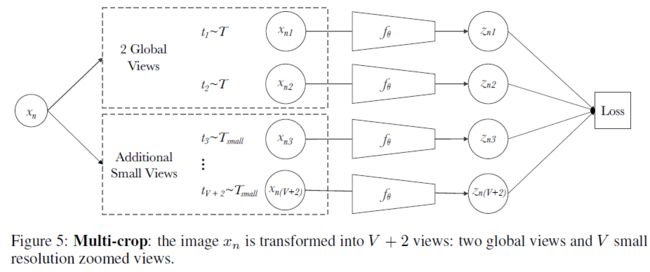 损失函数也由此推广为下式:
损失函数也由此推广为下式:
L ( z t 1 , z t 2 , … , z t V + 2 ) = ∑ i ∈ { 1 , 2 } ∑ v = 1 V + 2 1 v ≠ i ℓ ( z t v , q t i ) L\left(\mathbf{z}_{t_{1}}, \mathbf{z}_{t_{2}}, \ldots, \mathbf{z}_{t_{V+2}}\right)=\sum_{i \in\{1,2\}} \sum_{v=1}^{V+2} \mathbf{1}_{v \neq i} \ell\left(\mathbf{z}_{t_{v}}, \mathbf{q}_{t_{i}}\right) L(zt1,zt2,…,ztV+2)=i∈{1,2}∑v=1∑V+21v=iℓ(ztv,qti) - Multi-crop is a very general trick to improve self-supervised learning representations
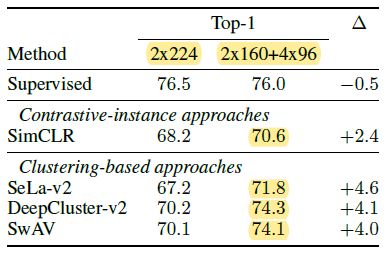
在不加 multi-crop 之前,SWAV 其实还不如 MoCov2,也就是说这种聚类和对比学习结合的方法其实并没有什么优势,真正提点的是 multi-crop,而且由于 multi-crop 的普适性,接下来的很多工作借鉴的基本都是 multi-crop 而非 SWAV 这篇工作本身
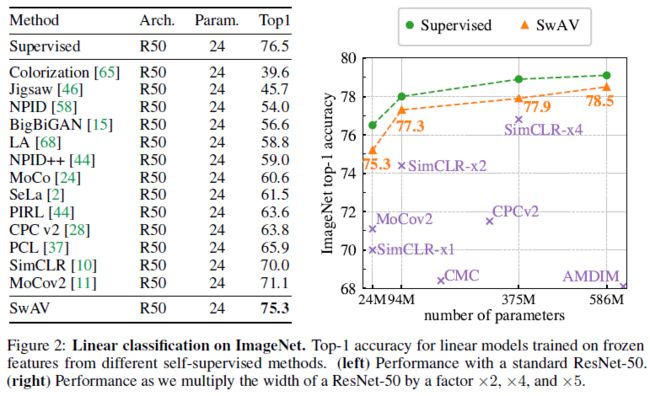
Linear classification on ImageNet
第三阶段:不用负样本
- 负样本在对比学习中是十分重要的。假如模型在学习时只有正样本,那么模型就很容易学到一条捷径,让所有的输入都有相同的输出从而使正样本特征完全相同 (i.e. model collapse / learning collapse / mode collapse),而负样本的加入就可以避免模型坍塌的发生
- 但下面的工作就比较另辟蹊径,完全没有使用负样本,只使用正样本进行学习居然也可以取得不错的效果
BYOL (Bootstrap Your Own Latent)
- paper: Bootstrap Your Own Latent: A New Approach to Self-Supervised Learning
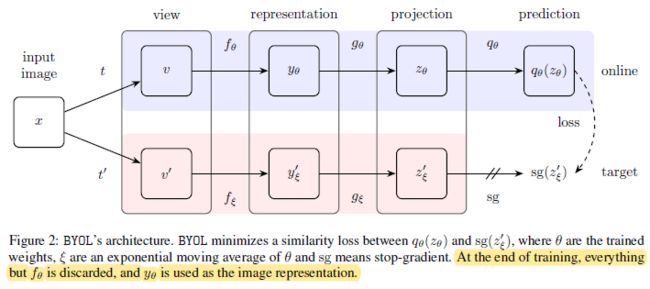
Latent: 特征;Bootstrap Your Own Latent: 自己跟自己学,左脚踩右脚就上天了!
sg: stop graient
- 如上图所示,BYOL 整体结构类似 MoCov2,由一个 query encoder (紫色部分) 和一个 key encoder (蓝色部分) 组成, query encoder 和 key encoder 的前两部分结构完全相同 (i.e. backbone f f f and projection head g g g),key encoder 采用动量更新
- 特别的是,BYOL 创造了一个不需要负样本的代理任务:BYOL 在 query encoder 后新增了一个 predictor q θ q_\theta qθ, q θ q_\theta qθ 的结构与 projection head g θ g_\theta gθ 完全相同,也是一个 MLP。代理任务的目标是使得 predictor 的输出 q θ ( z θ ) q_\theta(z_\theta) qθ(zθ) 与 key encoder 的输出 z ξ ′ z_\xi' zξ′ 尽可能一致,损失函数就直接使用均方误差 MSE loss。通过这个代理任务,BYOL 将原来的匹配问题转换为了预测问题 (其实和 SWAV 有些类似,但 BYOL 甚至没有借助聚类中心),相当于用自己一个视角的特征去预测另外一个视角的特征,通过预测型的任务来完成模型训练
针对 BYOL 的博客和他们的回应
- blog: Understanding Self-Supervised and Contrastive Learning with “Bootstrap Your Own Latent” (BYOL)
- paper: BYOL works even without batch statistics
- 这篇博客的产生非常有意思,是博客作者在自己复现 BYOL 时遗漏了一个小细节,从而导致他的模型产生了模型坍塌,而这个细节又与 batch norm 有关!(回忆一下,MoCo 里的 batch norm 也惹事儿了,最终被 Shuffling BN 所替代) 最终在进行一系列消融实验后作者发现,
- (1) BYOL 在不使用 BN 时性能与随机网络差不多
- (2) BN 隐式地引入了对比学习
- 作者认为,以上的两个发现依然强调了对比学习中正负样本对比的重要性
Projection heads in SOTA self-supervised methods
Surprising results
- 正是由于上面所说的 Projection heads 的小小差别造成了这次发现。博客作者是基于 MoCo 代码进行的复现,而 MoCo 的 projection head 中并没有使用 BN,而这点小小的区别竟然导致训练出的网络性能与随机网络相似

- 基于上述实验结果,作者认为在不使用对比损失的情况下,BYOL 的成功之处在于 projection heads 中使用的 BN 泄露了同批次中其他样本的信息,这等同于模型进行了隐式的对比学习
Why batch normalization is critical in BYOL: mode collapse
- 无论 BN 层的输入多么相似,输出都会根据 running mean 和 running var 进行重新归一化 (redistribute the activations through vector space) 从而防止 mode collapse
Why BN is implicit contrastive learning: all examples are compared to the mode
- BN 在进行归一化时需要计算 mini-batch 内所有样本的均值和方差,因此 BYOL 在计算正样本 loss 时其实也看到了其他样本的特征。由于这种信息泄露的存在,mini-batch 中的其他样本就可以看作是隐式的负样本
- 换句话说,BN 使得 BYOL 并不只是正样本在自己跟自己学,它其实也在对比正样本和平均图片 (mode / average image) 有什么区别 (“how is this image different from the average image?”)
BYOL 作者的回应:BYOL works even without batch statistics!
- 作者发现 BN 确实是比较关键,只要 Encoder、Projector、Predictor 都不使用 BN,BYOL 就会产生训练坍塌。但作者同时也找到了几个特例:(1) 当只有 Projector 使用 BN 时,BYOL 的训练还是失败了,作者认为如果 BN 有提供隐式负样本的能力,那这种情况就不应该训练失败;(2) 当 Encoder 和 Projector 都不使用 BN 或 LN 时,SimCLR 也失败了 (SimCLR 没有 Predictor),也就是说在这种情况下即使给定显式的负样本也训练不出来。由于上面两个特例的存在,作者就觉得 BN 主要的作用还是帮助模型稳定训练,从而防止模型坍塌,而不是提供隐式负样本
- 于是,作者又作了进一步的实验,对所有卷积和线性层参数使用 WS (Weight Standardization),并且把所有 BN 层换成 GN (Group Normalization) 层,最终在 1000 个 epochs 后达到了 73.9% top-1 accuracy。GN 和 WS 都没有使用 batch statistics,因此也就有效地驳斥了上述博客的观点
SimSiam (Simple Siamese)
- paper: Exploring Simple Siamese Representation Learning
SimSiam
- 从上面对比学习一路的发展历程可以看到,对比学习的性能似乎是由很多个 tricks 堆叠起来的,例如动量编码器、projection head、训练更长时间、更多的数据增强、multi-crop… 但这样就不利于我们分析对比学习的性能到底是由什么带来的。而 SimSiam 就把对比学习的整个过程化繁为简,(1) 不使用负样本;(2) 不使用更大的 batches;(3) 不使用动量编码器,最终也取得了很好的效果
- 如下图所示,SimSiam 结构与 BYOL 很相似,唯一的不同是 SimSiam 没有用动量编码器


Empirical Study
- 作者通过实验证明,之所以 SimSiam 能够成功训练而没有模型坍塌,主要就是因为有 stop gradient 操作的存在。如下图 1 所示,如果没有 stop gradient,优化器就会迅速找到一个退化解并达到最小的 training loss -1。为了进一步证明退化解是由模型坍塌产生的,作者研究了 encoder 的输出 z / ∣ ∣ z ∣ ∣ 2 z/||z||_2 z/∣∣z∣∣2 的标准差,如果出现了模型坍塌,那么输出的每个 channel 上的标准差为 0,图 2 证明了退化解的确是由模型坍塌带来的

Hypothesis
- 由上述实验结论作者提出了如下猜想:SimSiam 其实是一种 Expectation-Maximization (EM) 算法,它隐含了两个变量集合 (观测变量 + 隐变量),并且解决了两个子问题 (E 步 + M 步). stop gradient 操作的存在就是引入额外变量集合的结果
- 可以考虑如下损失函数:
 其中, θ \theta θ 为模型参数, T \mathcal{T} T 为数据增强, x x x 为图像。为了方便分析,损失函数使用均方误差,当向量为 l 2 \mathcal{l}_2 l2-normalized 时与基于余弦相似度的损失函数等价。同时,这里也暂时不考虑 predictor。注意到,在上述损失函数中,作者引入了一个额外的变量集合 η \eta η 用于表示图片的特征,它只是一个需要优化的参数而不一定是网络的输出, η \eta η 的大小与图片数量成正比, η x \eta_x ηx 为图片 x x x 的特征表示。因此,这个损失函数就是要让模型输出的经过图像增强后的图像特征与原有的图像特征尽可能相似
其中, θ \theta θ 为模型参数, T \mathcal{T} T 为数据增强, x x x 为图像。为了方便分析,损失函数使用均方误差,当向量为 l 2 \mathcal{l}_2 l2-normalized 时与基于余弦相似度的损失函数等价。同时,这里也暂时不考虑 predictor。注意到,在上述损失函数中,作者引入了一个额外的变量集合 η \eta η 用于表示图片的特征,它只是一个需要优化的参数而不一定是网络的输出, η \eta η 的大小与图片数量成正比, η x \eta_x ηx 为图片 x x x 的特征表示。因此,这个损失函数就是要让模型输出的经过图像增强后的图像特征与原有的图像特征尽可能相似 - 我们的目标是解如下的双变量优化问题:
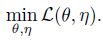 这个问题与 k-means 聚类类似,变量 θ \theta θ 可以看作聚类中心, η x \eta_x ηx 可以看作图片 x x x 的分配向量 (指示 x x x 属于哪个簇的 one-hot vector)。类似于 k-means,我们也可以通过解两个子问题来解决上述优化问题,也就是交替地固定一个变量集合并求另一个变量集合的最优解:
这个问题与 k-means 聚类类似,变量 θ \theta θ 可以看作聚类中心, η x \eta_x ηx 可以看作图片 x x x 的分配向量 (指示 x x x 属于哪个簇的 one-hot vector)。类似于 k-means,我们也可以通过解两个子问题来解决上述优化问题,也就是交替地固定一个变量集合并求另一个变量集合的最优解:
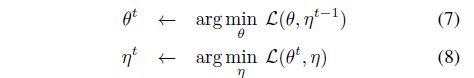
- Solving for θ θ θ: 可以用 SGD 解子问题 (7). 由于 η t − 1 \eta^{t-1} ηt−1 为一常量,stop-gradient 操作也就很自然地被引入了
- Solving for η η η: 每个 η x \eta_x ηx 都可以被独立优化,因此问题可以简化为对每张图片 x x x 解如下优化问题:
η x t ← arg min η x E T [ ∥ F θ t ( T ( x ) ) − η x ∥ 2 2 ] \eta^{t}_x \leftarrow \arg \min _{\eta_x} \mathbb{E}_{ \mathcal{T}}\left[\left\|\mathcal{F}_{\theta^t}(\mathcal{T}(x))-\eta_{x}\right\|_{2}^{2}\right] ηxt←argηxminET[∥Fθt(T(x))−ηx∥22]令梯度为 0 可得
 这表明 η x t \eta_x^t ηxt 为 average representation of x x x over the distribution of augmentation.
这表明 η x t \eta_x^t ηxt 为 average representation of x x x over the distribution of augmentation.
- One-step alternation: η x t \eta_x^t ηxt 的解为 T \mathcal T T 的期望,但求此期望是不现实的,因此可以使用一个近似,也就是只进行一次采样:
 其中, T ′ \mathcal T' T′ 为采样得到的数据增强方式。将上述解代入子问题 (7) 中可得
其中, T ′ \mathcal T' T′ 为采样得到的数据增强方式。将上述解代入子问题 (7) 中可得
 上式与 SimSiam 的结构相吻合 (without predictor),如果在使用 SGD 优化 θ \theta θ 时只进行一次梯度下降,那么我们就得到了 SimSiam 算法:a Siamese network naturally with stop-gradient applied。为了进一步验证上述猜想,作者把针对 θ \theta θ 的 one-step 优化扩展到了 multi-step 的优化 (提前将 k k k SGD steps 中需要的 η x \eta_x ηx 缓存在内存中),发现所有的 multi-step 变种都有不错的效果,有的甚至超过了原始的 SimSiam (one-step),这说明 alternating optimization 是一个有效的猜想,而 SimSiam 只是其中的一个特例:
上式与 SimSiam 的结构相吻合 (without predictor),如果在使用 SGD 优化 θ \theta θ 时只进行一次梯度下降,那么我们就得到了 SimSiam 算法:a Siamese network naturally with stop-gradient applied。为了进一步验证上述猜想,作者把针对 θ \theta θ 的 one-step 优化扩展到了 multi-step 的优化 (提前将 k k k SGD steps 中需要的 η x \eta_x ηx 缓存在内存中),发现所有的 multi-step 变种都有不错的效果,有的甚至超过了原始的 SimSiam (one-step),这说明 alternating optimization 是一个有效的猜想,而 SimSiam 只是其中的一个特例:

- Predictor h h h: 设 encoder f f f 的输出为 z z z,那么在 SimSiam 中, h h h 就是在最小化 E z [ ∣ ∣ h ( z 1 ) − z 2 ∣ ∣ 2 2 ] \mathbb E_z\left[||h(z_1)-z_2||_2^2\right] Ez[∣∣h(z1)−z2∣∣22],因此最优的 h h h 对每张图片 x x x 都满足 h ( z 1 ) = E z [ z 2 ] = E T [ f ( T ( x ) ) ] h(z_1)=\mathbb E_z[z_2]=\mathbb E_\mathcal{T}[f(\mathcal T(x))] h(z1)=Ez[z2]=ET[f(T(x))],这与子问题 η x t \eta_x^t ηxt 的解很相似。在 One-step alternation 中,我们只用了一次采样来近似期望值,作者猜想 h h h 的作用就是缩小了采样和期望之间的 gap,用于预测真实的期望值。为了验证该猜想的正确性,作者采用了其他方法来近似期望值:类似 InstDisc 中的 Memory bank,使用 moving-average 来更新 η x t \eta_x^t ηxt:
 该方法最终精度为 55.0%. 相比之下,如果不使用 predictor 和 moving-average,模型就会直接崩溃
该方法最终精度为 55.0%. 相比之下,如果不使用 predictor 和 moving-average,模型就会直接崩溃 - Symmetrization (对称 loss): 上述分析中并没有考虑对称 loss 的影响。作者认为,对称 loss 就相当于是在下式中对 T \mathcal T T 进行了密集采样,
 SGD 就相当于是在使用一个 batch 的图像和一对数据增强方法 ( T 1 , T 2 ) (\mathcal T_1,\mathcal T_2) (T1,T2) 来计算 empirical expectation E x , T \mathbb E_{x,\mathcal T} Ex,T,因此对称 loss 带来的密集采样会提高模型精度
SGD 就相当于是在使用一个 batch 的图像和一对数据增强方法 ( T 1 , T 2 ) (\mathcal T_1,\mathcal T_2) (T1,T2) 来计算 empirical expectation E x , T \mathbb E_{x,\mathcal T} Ex,T,因此对称 loss 带来的密集采样会提高模型精度

作者的猜想着重解释了 SimSiam 可能在进行的优化问题,而对于 SimSiam 为什么没有发生模型崩溃,作者给出了一些简单的看法:
The alternating optimization provides a different trajectory, and the trajectory depends on the initialization. It is unlikely that the initialized η η η, which is the output of a randomly initialized network, would be a constant. Starting from this initialization, it may be difficult for the alternating optimizer to approach a constant η x η_x ηx for all x x x, because the method does not compute the gradients w.r.t. η η η jointly for all x x x.
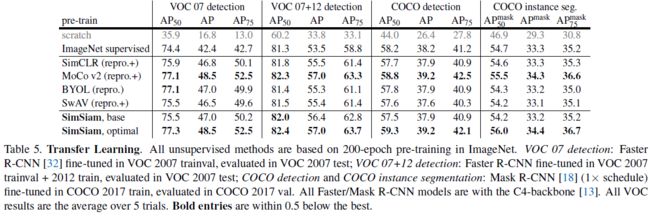
Comparisons
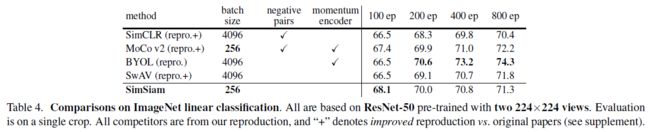
可以看到,MoCo v2 和 SimSiam 在迁移学习效果上表现是最好的
第四阶段:基于 Transformer
MoCov3
- paper: An Empirical Study of Training Self-Supervised Vision Transformers
- 作者主要研究了自监督训练 ViT 的稳定性,发现自监督的 ViT 在训练时的不稳定性其实极大地损害了模型性能。最终作者用一个小小的改进就让训练变得更加稳定
MoCo v3
- MoCo v3 其实就是 MoCo v2 和 SimSiam 的合体。相比 MoCo v2,(1) MoCo v3 的 query encoder 增加了 predictor (query encoder f q f_q fq = backbone (e.g. ResNet, ViT) + projection head + prediction head),(2) 并且作者发现当 batch size 足够大时 (e.g. 4096),memory queue 就没什么用了,因此 MoCo v3 抛弃了 memory queue,这也简化了模型代码,(3) 损失函数则采用 InfoNCE:
 其中,正样本 k + k^+ k+ 为 key encoder f k f_k fk 输出的同一图片另一个 view 的特征,负样本集 { k − } \{k^-\} {k−} 为 key encoder f k f_k fk 输出的同一 batch 内其他样本的特征。整体的目标函数使用的是和 SimSiam 类似的对称项:
其中,正样本 k + k^+ k+ 为 key encoder f k f_k fk 输出的同一图片另一个 view 的特征,负样本集 { k − } \{k^-\} {k−} 为 key encoder f k f_k fk 输出的同一 batch 内其他样本的特征。整体的目标函数使用的是和 SimSiam 类似的对称项:
c t r ( q k , k 1 ) + c t r ( q 2 , k 1 ) ctr(q_k,k_1)+ctr(q_2,k_1) ctr(qk,k1)+ctr(q2,k1) - 在 backbone 使用 ResNet 的情况下,MoCo v3 精度超过了之前的版本:
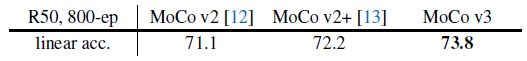 作者认为,这主要是源于额外的 prediction head 以及大 batch (4096) 训练
作者认为,这主要是源于额外的 prediction head 以及大 batch (4096) 训练
Stability of Self-Supervised ViT Training
- 如果将 MoCo v3 的网络 backbone 从 ResNet 换为 ViT,训练就会变得不稳定。下面首先分析哪些因素会对训练的稳定性产生影响:
- (1) Batch size: ViT 模型需要大量的算力,大 batch 对大 ViT 模型的训练是有好处的。此外,大 batch 能提供更多负样本,在自监督学习方法中效果也应该更好。因此,作者实验了不同 batch size 的训练效果,但发现当 batch size 比较大的时候模型训练就会变得不稳定,模型性能也更差

- (2) Learning rate: 在实践中,学习率通常随着 batch size 的增大而增大,因此作者采取了 linear scaling rule,即学习率设为 l r × B a t c h S i z e / 256 lr×BatchSize/256 lr×BatchSize/256。作者在之后实验了超参 l r lr lr 的影响,发现 l r lr lr 较小时模型更稳定,但也更容易欠拟合

- (3) Optimizer: 作者使用训练 ViT 常用的 AdamW 作为优化器
- (1) Batch size: ViT 模型需要大量的算力,大 batch 对大 ViT 模型的训练是有好处的。此外,大 batch 能提供更多负样本,在自监督学习方法中效果也应该更好。因此,作者实验了不同 batch size 的训练效果,但发现当 batch size 比较大的时候模型训练就会变得不稳定,模型性能也更差
- A Trick for Improving Stability: 在训练的时候,作者发现网络回传的梯度会出现 “spike”,这个 spike 会使得 training curve 有一个突然的下降,并且 spike 每次都是先发生在第一层,也就是做 patch projection 的时候 (i.e. patch embedding),然后过了很多个迭代后传导到最后一层。因此可以认为,训练不稳定是模型浅层引起的
 基于上述发现,作者在训练的时候就直接冻结 patch projection layer,也就是压根不训练 patch projection layer,这个 trick 还真的使得训练更稳定,模型性能也更好了:
基于上述发现,作者在训练的时候就直接冻结 patch projection layer,也就是压根不训练 patch projection layer,这个 trick 还真的使得训练更稳定,模型性能也更好了:
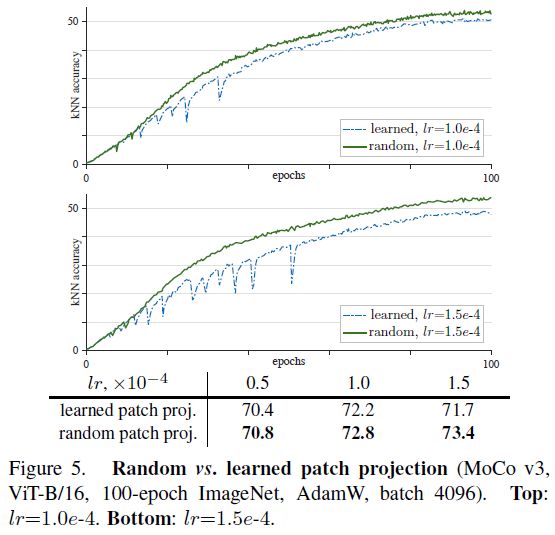 更加神奇的是,这个 trick 不光对 MoCo v3 有用,它对 SimCLR、BYOL、SWAV 等其他自监督方法也同样有用 (backbone 均为 ViT)
更加神奇的是,这个 trick 不光对 MoCo v3 有用,它对 SimCLR、BYOL、SWAV 等其他自监督方法也同样有用 (backbone 均为 ViT)

不过作者也提到,这个 trick 只是缓解了训练不稳定的问题,但并没有真正解决它,当学习率过大时,模型仍会变得不稳定
DINO (self-DIstillation with NO labels)
- paper: Emerging Properties in Self-Supervised Vision Transformers
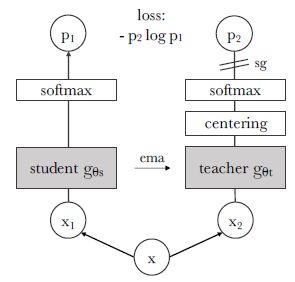
Self-distillation with no labels
- DINO 的结构并没有太多创新,与 BYOL 的结构非常类似,也是用一个 query encoder 和一个动量更新的 key encoder 进行预测任务的学习。主要的不同是为了避免模型坍塌而增加了 centering 操作,也就是先计算整个 batch 内样本的均值,然后所有样本再减去均值 (是不是和 BYOL 中有关 BN 作用的讨论有点像)
Self-attention from a Vision Transformer
References
- 对比学习论文综述【论文精读】
- Understanding SWAV: self-supervised learning with contrasting cluster assignments