BFS算法-leetcode java题解
BFS算法-leetcode java题解
本文目录
-
- BFS算法-leetcode java题解
-
- BFS算法思想
- leetcode 111. 二叉树的最小深度
- leetcode 1091. 二进制矩阵中的最短路径
- leetcode 752. 打开转盘锁
- leetcode 127. 单词接龙
- leetcode 433. 最小基因变化
- leetcode 1162. 地图分析
- leetcode 695. 岛屿的最大面积
- leetcode 207. 课程表
- leetcode 210. 课程表 II
- 双向BFS
- leetcode 752. 打开转盘锁 双向bfs
- leetcode 433. 最小基因变化 双向bfs
BFS算法思想
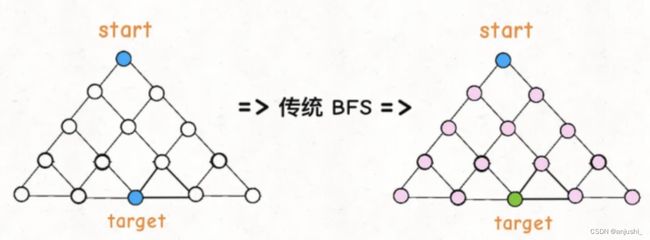
BFS的核心思想:把一些问题抽象成图,从一个点开始,向四周开始扩散。
一般来说,BFS算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度比 DFS 大很多
BFS问题的本质就是在一幅「图」中找到从起点start到终点target的最近距离
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
Queue q; // 核心数据结构
Set visited; // 避免走回头路
q.offer(start); // 将起点加入队列
visited.add(start);
int step = 0; // 记录扩散的步数
while (!q.isEmpty()) {
int sz = q.size();
/* 将当前队列中的所有节点向四周扩散 */
for (int i = 0; i < sz; i++) {
Node cur = q.poll();
/* 划重点:这里判断是否到达终点 */
if (cur is target)
return step;
/* 将 cur 的相邻节点加入队列 */
for (Node x : cur.adj())
if (x not in visited) {
q.offer(x);
visited.add(x);
}
}
/* 划重点:更新步数在这里 */
step++;
}
}
BFS 的核心数据结构;cur.adj()泛指cur相邻的节点,比如说二维数组中,cur上下左右四面的位置就是相邻节点;visited的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要visited
leetcode 111. 二叉树的最小深度

给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
输入:root = [3,9,20,null,null,15,7]
输出:2
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
public int minDepth(TreeNode root) {
if (root == null) return 0;
int depth = 1;
Queue queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int sz = queue.size();
for (int i = 0; i < sz; i++) {
TreeNode cur = queue.poll();
if (cur.left == null && cur.right == null)
return depth;
if (cur.left != null)
queue.offer(cur.left);
if (cur.right != null)
queue.offer(cur.right);
}
depth ++;
}
return depth;
}
leetcode 1091. 二进制矩阵中的最短路径
给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。
二进制矩阵中的 畅通路径 是一条从 左上角 单元格(即,(0, 0))到 右下角 单元格(即,(n - 1, n - 1))的路径,该路径同时满足下述要求:
路径途经的所有单元格都的值都是 0 。
路径中所有相邻的单元格应当在 8 个方向之一 上连通(即,相邻两单元之间彼此不同且共享一条边或者一个角)。
畅通路径的长度 是该路径途经的单元格总数。
输入:grid = [[0,1],[1,0]]
输出:2
输入:grid = [[0,0,0],[1,1,0],[1,1,0]]
输出:4
public static int shortestPathBinaryMatrix(int[][] grid) {
if(grid == null || grid.length == 0 || grid[0].length == 0){
return -1;
}
if(grid[0][0] == 1){
return -1;
}
int[][] directions = {{-1, -1}, {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}};//定义 8个方向
//bfs的老套路 来个队列,数据结构为数组int[]
Queue queue = new LinkedList<>();
int m = grid.length, n = grid[0].length;
queue.add(new int[]{0, 0});//把起点扔进去
grid[0][0] = 1;// 因为从出发点开始找寻路径,所以出发点不能再被经过,将其设为1
int step = 1;
while(!queue.isEmpty()){
int sz = queue.size();
for(int i = 0; i < sz; i++){ // 依次取出队列的每个节点并进行遍历
int[] cur = queue.poll();
// 如果等于终点则返回
if(cur[0] == m - 1 && cur[1] == n - 1){
return step;
}
// 对于当前节点,对其8个方向进行搜寻
for(int[] d : directions){
int row = cur[0] + d[0];
int col = cur[1] + d[1];//当前节点的某个方向上的节点坐标
if(row < 0 || row >= m || col < 0 || col >= n || grid[row][col] == 1){
continue;
}
queue.add(new int[]{row, col});
grid[row][col] = 1;// 某方向的节点被经历过后,将其标记为1,以后不再经过它
}
}
step++;// 一轮队列遍历完以后,即节点周围的一层节点被遍历完以后,路径长度+1
}
return -1;
}
leetcode 752. 打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出解锁需要的最小旋转次数,如果无论如何不能解锁,返回 -1 。
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。
输入: deadends = ["8888"], target = "0009"
输出:1
解释:把最后一位反向旋转一次即可 "0000" -> "0009"。
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:无法旋转到目标数字且不被锁定。
class Solution {
public int openLock(String[] deadends, String target) {
Set dead = new HashSet<>();
for(String d: deadends){
dead.add(d);
}
if (dead.contains("0000")) {
return -1;
}
Queue queue = new LinkedList<>();
Set visited = new HashSet<>();
queue.offer("0000");
visited.add("0000");
int path = 0;
while(!queue.isEmpty()){
int sz = queue.size();
for(int i = 0; i < sz; i++){
String cur = queue.poll();
if(cur.equals(target)){
return path;
}
for(int j = 0; j < cur.length(); j++){
String str = plusOne(cur, j);
if(!visited.contains(str) && !dead.contains(str)){
queue.offer(str);
visited.add(str);
}
String strr = minusOne(cur, j);
if(!visited.contains(strr) && !dead.contains(strr)){
queue.offer(strr);
visited.add(strr);
}
}
}
path ++;
}
return -1;
}
public String plusOne(String cur, int j){
char[] ch = cur.toCharArray();
if(ch[j] == '9'){
ch[j] = '0';
}else{
ch[j] ++;
}
return String.valueOf(ch);
}
public String minusOne(String cur, int j){
char[] ch = cur.toCharArray();
if(ch[j] == '0'){
ch[j] = '9';
}else{
ch[j] --;
}
return String.valueOf(ch);
}
}
leetcode 127. 单词接龙
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。
sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0
输入:beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出:5
解释:一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。
public int ladderLength(String beginWord, String endWord, List wordList) {
if(!wordList.contains(endWord) || beginWord.length() != endWord.length()){
return 0;
}
Set path = new HashSet<>();
for(String s: wordList){
path.add(s);
}
Queue queue = new LinkedList<>();
Set hasUsed = new HashSet<>();
queue.offer(beginWord);
hasUsed.add(beginWord);
int road = 1;
while(!queue.isEmpty()){
int sz = queue.size();
for(int i = 0; i < sz; i++){
String cur = queue.poll();
if(cur.equals(endWord)){
return road;
}
for(int j = 0; j < beginWord.length(); j++){
List newWords = changeWord(cur, j, path);
for (String nei : newWords) {
if (!hasUsed.contains(nei)) {
queue.offer(nei);
hasUsed.add(nei);
}
}
}
}
road ++;
}
return 0;
}
public List changeWord(String cur, int j, Set path){
List res = new LinkedList<>();
char[] chstr = cur.toCharArray();
for(char ch = 'a'; ch <= 'z'; ch ++){
if(ch == cur.charAt(j)){
continue;
}
chstr[j] = ch;
String newS = String.valueOf(chstr);
if(path.contains(newS))
res.add(newS);
}
return res;
}
leetcode 433. 最小基因变化
基因序列可以表示为一条由 8 个字符组成的字符串,其中每个字符都是 'A'、'C'、'G' 和 'T' 之一。
假设我们需要调查从基因序列 start 变为 end 所发生的基因变化。一次基因变化就意味着这个基因序列中的一个字符发生了变化。
例如,"AACCGGTT" --> "AACCGGTA" 就是一次基因变化。
另有一个基因库 bank 记录了所有有效的基因变化,只有基因库中的基因才是有效的基因序列。(变化后的基因必须位于基因库 bank 中)
给你两个基因序列 start 和 end ,以及一个基因库 bank ,请你找出并返回能够使 start 变化为 end 所需的最少变化次数。如果无法完成此基因变化,返回 -1 。
注意:起始基因序列 start 默认是有效的,但是它并不一定会出现在基因库中。
输入:start = "AACCGGTT", end = "AACCGGTA", bank = ["AACCGGTA"]
输出:1
输入:start = "AACCGGTT", end = "AAACGGTA", bank = ["AACCGGTA","AACCGCTA","AAACGGTA"]
输出:2
输入:start = "AAAAACCC", end = "AACCCCCC", bank = ["AAAACCCC","AAACCCCC","AACCCCCC"]
输出:3
public int minMutation(String startGene, String endGene, String[] bank) {
Set path = new HashSet<>();
for(String s : bank){
path.add(s);
}
Queue queue = new LinkedList<>();
Set hasUsed = new HashSet<>();
queue.offer(startGene);
hasUsed.add(startGene);
int res = 0;
char[] keys = {'A', 'C', 'G', 'T'};
while(!queue.isEmpty()){
int sz = queue.size();
for(int i = 0; i < sz; i++){
String cur = queue.poll();
if(endGene.equals(cur)){
return res;
}
for(int j = 0; j < startGene.length(); j++){
List temp = changeOne(cur, j, keys);
for(String cc: temp){
if(path.contains(cc) && !hasUsed.contains(cc)){
queue.offer(cc);
hasUsed.add(cc);
}
}
}
}
res ++;
}
return -1;
}
// A C G T => 0,1,2,3
public List changeOne(String cur, int j, char[] keys){
List list = new LinkedList<>();
char[] ch = cur.toCharArray();
for(int i = 0; i <= 3; i++){
if(ch[j] == keys[i]){
continue;
}else{
ch[j] = keys[i];
}
list.add(String.valueOf(ch));
}
return list;
}
leetcode 1162. 地图分析
你现在手里有一份大小为 n x n 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地。
请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的,并返回该距离。如果网格上只有陆地或者海洋,请返回 -1。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
输入:grid = [[1,0,1],[0,0,0],[1,0,1]]
输出:2
解释:
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大,最大距离为 2。
public static int maxDistance(int[][] grid) {
Queue queue = new LinkedList<>();
int flag = 0;
for(int i = 0; i < grid.length; i++){
for(int j = 0; j < grid[0].length; j++){
if(grid[i][j] == 1){
queue.offer(new int[]{i, j});
flag ++;
}
}
}
if(flag == grid.length * grid[0].length){
return -1;
}
int[][] d = {{0,1}, {0,-1}, {1,0}, {-1,0}};
int[] point = null;
while(!queue.isEmpty()){
int sz = queue.size();
for(int i = 0; i < sz; i++){
point = queue.poll();
for(int j = 0; j < d.length; j++){
int row = point[0] + d[j][0];
int col = point[1] + d[j][1];
if(row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] != 0){
continue;
}
queue.add(new int[]{row, col});
grid[row][col] = grid[point[0]][point[1]] + 1;
}
}
}
if (point == null) {
return -1;
}
return grid[point[0]][point[1]] - 1;
}
leetcode 695. 岛屿的最大面积
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
public int maxAreaOfIsland(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(grid[i][j] == 1){
res = Math.max(res, bfs(grid, i, j));
}
}
}
return res;
}
public int bfs(int[][] grid, int i, int j){
int[][] d = new int[][]{{1,0},{0,1},{-1,0},{0,-1}};
Queue queue = new LinkedList<>();
queue.offer(new int[]{i,j});
grid[i][j] = 0;
int dis = 1;
while(!queue.isEmpty()){
int sz = queue.size();
for(int x = 0; x < sz; x++){
int[] cur = queue.poll();
for(int y = 0; y < 4; y ++){
int a = cur[0] + d[y][0];
int b = cur[1] + d[y][1];
if(a >= 0 && a < grid.length && b >= 0 && b < grid[0].length && grid[a][b] == 1){
grid[a][b] = 0;
queue.offer(new int[]{a,b});
dis ++;
}
}
}
}
return dis;
}
leetcode 207. 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
使用图的邻接矩阵存储,入度为0的点没有前驱节点
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] inDegree = new int[numCourses]; // 存储入度
Map> map = new HashMap<>(); // 构建邻接表
// 初始化入度和邻接表
for (int i = 0; i < prerequisites.length; i++) {
inDegree[prerequisites[i][0]]++; // 记录入度
if (map.containsKey(prerequisites[i][1])) { // 加入邻接表
map.get(prerequisites[i][1]).add(prerequisites[i][0]);
} else {
List list = new ArrayList<>();
list.add(prerequisites[i][0]);
map.put(prerequisites[i][1], list);
}
}
Queue queue = new LinkedList<>();
int count = 0;
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] == 0) {
queue.add(i);
}
}
while (!queue.isEmpty()) {
int sz = queue.size();
for(int i = 0; i < sz; i++){
count ++;
int cur = queue.poll();
List list = map.get(cur);
if (list == null) continue;
for (int j = 0; j < list.size(); j++) {
inDegree[list.get(j)] --;
if (inDegree[list.get(j)] == 0) {
queue.offer(list.get(j));
}
}
}
}
return count == numCourses;
}
}
leetcode 210. 课程表 II
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
只记录入度,每次都去遍历数组,减入度,减到0则加入路径
public static int[] findOrder(int numCourses, int[][] prerequisites) {
int[] inDegree = new int[numCourses]; // 存储入度
for (int i = 0; i < prerequisites.length; i++) {
inDegree[prerequisites[i][0]]++; // 记录入度
}
Queue queue = new LinkedList<>();
int count = 0;
for (int i = 0; i < numCourses; i++) {
if (inDegree[i] == 0) {
queue.add(i);
}
}
int[] path = new int[numCourses]; // 可以学完的课程
while (!queue.isEmpty()) {
int sz = queue.size();
for(int i = 0; i < sz; i++){
int cur = queue.poll();
path[count] = cur;
count ++;
for (int[] p : prerequisites) {
if (p[1] == cur){
inDegree[p[0]]--;
if (inDegree[p[0]] == 0){
queue.offer(p[0]);
}
}
}
}
if(count == numCourses){
break;
}
}
if(count == numCourses){
return path;
}else{
return new int[]{};
}
}
双向BFS
双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离,双向 BFS 比传统 BFS 高效
双向 BFS 也有局限,因为你必须知道终点在哪里
leetcode 752. 打开转盘锁 双向bfs
public static int openLock(String[] deadends, String target) {
Set deads = new HashSet<>();
for (String s : deadends) deads.add(s);
// 用集合不用队列,可以快速判断元素是否存在
Set q1 = new HashSet<>();
Set q2 = new HashSet<>();
Set visited = new HashSet<>();
int step = 0;
q1.add("0000");
q2.add(target);
while (!q1.isEmpty() && !q2.isEmpty()) {
// 哈希集合在遍历的过程中不能修改,用 temp 存储扩散结果
Set temp = new HashSet<>();
/* 将 q1 中的所有节点向周围扩散 */
for (String cur : q1) {
/* 判断是否到达终点 */
if (deads.contains(cur))
continue;
if (q2.contains(cur))
return step;
visited.add(cur);
/* 将一个节点的未遍历相邻节点加入集合 */
for (int j = 0; j < 4; j++) {
String up = plusOne(cur, j);
if (!visited.contains(up))
temp.add(up);
String down = minusOne(cur, j);
if (!visited.contains(down))
temp.add(down);
}
}
/* 在这里增加步数 */
step++;
// temp 相当于 q1
// 这里交换 q1 q2,下一轮 while 就是扩散 q2
q1 = q2;
q2 = temp;
}
return -1;
}
- 使用 HashSet 方便快速判断两个集合是否有交集**
- while 循环的最后交换q1和q2的内容,所以只要默认扩散q1就相当于轮流扩散q1和q2
双向 BFS 优化
// ...
while (!q1.isEmpty() && !q2.isEmpty()) {
if (q1.size() > q2.size()) {
// 交换 q1 和 q2
temp = q1;
q1 = q2;
q2 = temp;
}
}
按照 BFS 的逻辑,队列(集合)中的元素越多,扩散之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些
leetcode 433. 最小基因变化 双向bfs
public static int minMutation(String startGene, String endGene, String[] bank) {
Set path = new HashSet<>();
for(String s : bank){
path.add(s);
}
if(!path.contains(endGene)){
return -1;
}
Set q1 = new HashSet<>();
Set q2 = new HashSet<>();
Set hasUsed = new HashSet<>();
q1.add(startGene);
q2.add(endGene);
hasUsed.add(startGene);
int res = 0;
char[] keys = {'A', 'C', 'G', 'T'};
while(!q1.isEmpty() && !q2.isEmpty()){
Set temp = new HashSet<>();
for(String cur: q1){
if (q2.contains(cur)){
return res;
}
hasUsed.add(cur);
for(int j = 0; j < startGene.length(); j++){
List nowList = changeOne(cur, j, keys);
for(String cc: nowList){
if(path.contains(cc) && !hasUsed.contains(cc)){
temp.add(cc);
}
}
}
}
res ++;
q1 = q2;
q2 = temp;
}
return -1;
}
// A C G T => 0,1,2,3
public static List changeOne(String cur, int j, char[] keys){
List list = new LinkedList<>();
char[] ch = cur.toCharArray();
for(int i = 0; i < 4; i++){
if(ch[j] == keys[i]){
continue;
}else{
ch[j] = keys[i];
}
list.add(String.valueOf(ch));
}
return list;
}