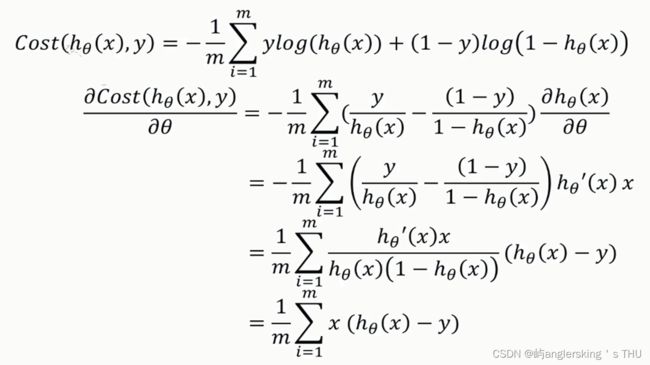机器学习三逻辑回归

---

前言

逻辑回归不同于线性回归，和多元线性回归。它解决的是分类问题，其中需要注意的是要将G（x） h（x）变为sigmoid函数，因为阶跃函数没有梯度下降，不能用于预测。sigmoid可导连续可以用梯度下降。
逻辑回归不是回归
其实质是做分类任务
垃圾邮件分类
预测肿瘤良性还是恶性
商家预测用户是否购物

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、逻辑回归代价函数

合并的

二、梯度下降函数

1.例子代码

代码如下（示例）：

import numpy as np
import matplotlib.pyplot as plt
data = np.genfromtxt('LRdata.txt',delimiter=',')
x_data = data[:,:-1]
y_data = data[:,-1]
x_data = np.concatenate((np.ones((100,1)),x_data),axis=1)
x_cord1 = []
y_cord1 = []
x_cord2 = []
y_cord2 = []
for i in range(len(y_data)):
    if(y_data[i]==0):
        x_cord1.append(x_data[i,1])
        y_cord1.append(x_data[i,2])
    else:
        x_cord2.append(x_data[i,1])
        y_cord2.append(x_data[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x_cord1,y_cord1,s=15,c='red',marker='s')
ax.scatter(x_cord2,y_cord2,s=15,c='green',marker='o')

plt.show()

maxcounter = 500

def sigmod(x):
    return 1.0/(1+np.exp(-x))

costList = []

def costFunc(x_data,y_data,theta):
    a = -y_data*np.log(sigmod(np.dot(x_data,theta)))
    b = -(1-y_data)*np.log(1-sigmod(np.dot(x_data,theta)))
    sum = a+b
    sum = np.sum(sum)
    return sum/len(x_data)

def gradacent(x_data,y_data):
    alf = 0.001
    m,n = np.shape(x_data)
    theta  = np.ones((n,1))
    y_data = np.array(y_data).reshape((m,1))

    for i in range(maxcounter):
        h = sigmod(np.dot(x_data,theta))
        err = (np.dot(x_data.T,(h - y_data)))*(1/m)
        theta = theta - alf*err
        costList.append(costFunc(x_data,y_data,theta))
    return theta

theta_p = gradacent(x_data,y_data)

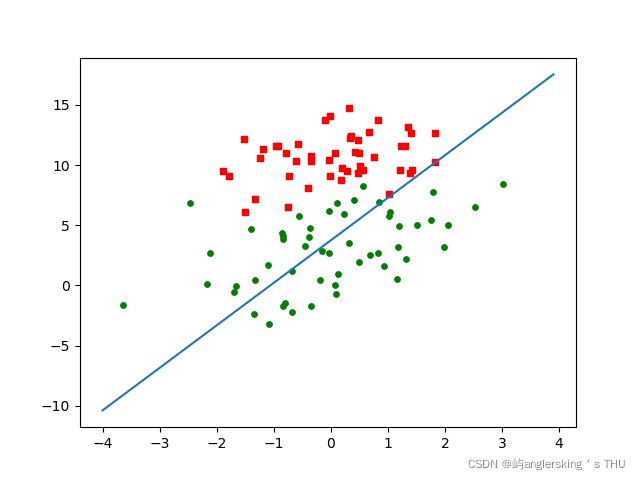
plt.scatter(x_cord1,y_cord1,s=15,c='red',marker='s')
plt.scatter(x_cord2,y_cord2,s=15,c='green',marker='o')

x1 = np.arange(-4,4,0.1)
x2 = (-theta_p[0]-theta_p[1]*x1)/theta_p[2]

plt.plot(x1,x2)
plt.show()

x = np.linspace(0,maxcounter,maxcounter)
plt.plot(x,costList)

plt.show()

运行结果