SoftTriple Loss: Deep Metric Learning Without Triplet Sampling
推荐视频:北大应用数学基础 张志华主讲 在前面介绍部分的图都来自与本视频
在介绍本论文之前,先看一下“前辈”
Triplet loss 刚开始应用在了人脸上


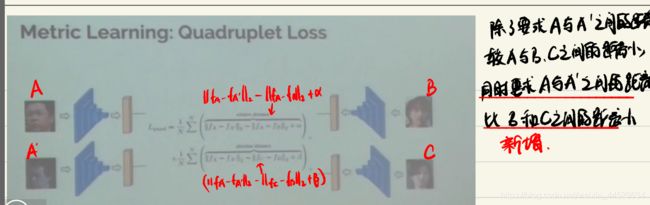

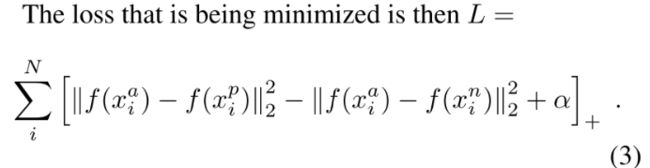
note:对于easy triplet,Loss=0(a-p的距离+ α \alpha α < a-n的距离),所以绝大多数样本对训练来说是没有意义的,不易收敛。
所以要设计一个采样策略,在FaceNet这篇论文中使用了online semi-hard negative sampling strategy,在easy triplet(Loss=0,对训练无意义)和hardest triplet(lead to bad local minima early on in training)(后面很多论文都是基于如何设计一个比较好的sampling strategy)
其中,semi-hard negative满足如下的条件

下面主要介绍了hard sample mining的流程图(not semi-hard negative)

combining classification and metric learning always perform better! to do!
接下来看一下本文如何结合softmax实现softTiplet loss
Abstract
distance metric leaning主要是让相同类的embedding 比不同类的embedding closer。
Our analysis shows that SoftMax loss is equivalent to a smoothed triplet loss where each class has a single center.
但在现实场景中,一个类会包含多个center,如下图中一种鸟(fine-grain)会存在多个聚类中心,比如头部和翅膀等,基于此,propose the SoftTriple loss to extend the SoftMax loss with multiple centers for each class.
优点:without the sampling phase by mildly increasing the size of the last fully connected layer.
实验数据集:fine-grained dataset
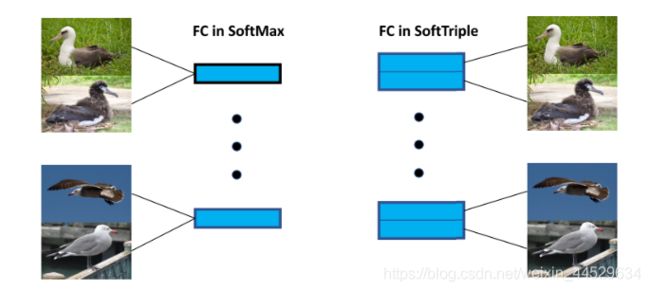
3. SoftTriple Loss
本节主要是介绍SoftMax loss和triplet loss,在学习完他们之间的联系后推导出SoftTriple loss.
首先,Softmax operator:
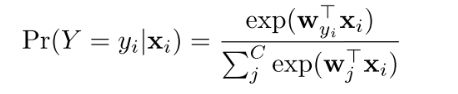
然后 softmax loss:

(以上公式比较常见,具体符号说明见论文,此处省略)
给定 ( x i , x j , x k ) (x_i,x_j,x_k) (xi,xj,xk),其目标为同类embedding的距离比不同类的更近:( δ \delta δ是一个margin)
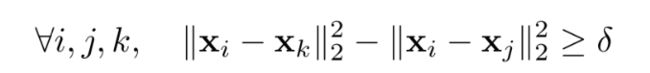
转换为相似度时:(each example has the unit length. ∣ ∣ x ∣ ∣ 2 = 1 ||x||_2=1 ∣∣x∣∣2=1)

tripet loss:
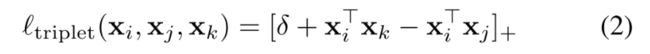
normalized SoftMax loss: λ \lambda λ是个平滑项
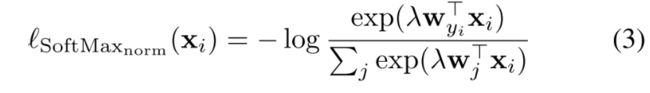

之后,根据KKT条件解出p的概率分布:
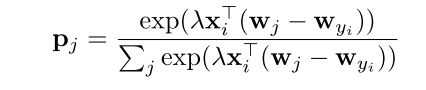
3.1. Multiple Centers
此时假设每个class有K个center,首先求出关于 x i x_i xi相似度最大的center(个人理解:此时选定一个center后就可以应用上述softmax的相关内容)
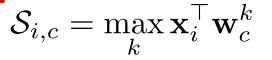
约束:

加个margin:

improve the robustness by smoothing the max operator.

3.2. Adaptive Number of Centers

其实整篇论文就是结合softmax的思想实现多center的triplet loss,综合最后推出来的loss来看,不需要设计复杂的sampling strategy。
下面是将公式写成代码的形式。
code:
class SoftTriple(nn.Module):
def __init__(self, la, gamma, tau, margin, dim, cN, K):
#la:lammbda20; gamma:0.1; tau:0.2; margin:0.01; dim:64; cN:class_num 98; K: center_num 10;
"""
:param la: Eq(8) lambda
:param gamma:
:param tau:
:param margin:
:param dim: dimensionality of embeddings.model的输出维度即为embedding
:param cN: class_num=98,数据集cars196
:param K: center_num=10
"""
super(SoftTriple, self).__init__()
self.la = la
self.gamma = 1./gamma
self.tau = tau
self.margin = margin
self.cN = cN
self.K = K
self.fc = Parameter(torch.Tensor(dim, cN*K))
self.weight = torch.zeros(cN*K, cN*K, dtype=torch.bool).cuda()
for i in range(0, cN):
for j in range(0, K):
self.weight[i*K+j, i*K+j+1:(i+1)*K] = 1
init.kaiming_uniform_(self.fc, a=math.sqrt(5))
return
def forward(self, input, target): #input为原始image通过bninception后的64维的embedding
centers = F.normalize(self.fc, p=2, dim=0) #对fc的weight进行normalize
simInd = input.matmul(centers) #相似度 Eq.5
simStruc = simInd.reshape(-1, self.cN, self.K)
prob = F.softmax(simStruc*self.gamma, dim=2)
simClass = torch.sum(prob*simStruc, dim=2)
marginM = torch.zeros(simClass.shape).cuda()
marginM[torch.arange(0, marginM.shape[0]), target] = self.margin
lossClassify = F.cross_entropy(self.la*(simClass-marginM), target)
if self.tau > 0 and self.K > 1:
simCenter = centers.t().matmul(centers)
reg = torch.sum(torch.sqrt(2.0+1e-5-2.*simCenter[self.weight]))/(self.cN*self.K*(self.K-1.))
return lossClassify+self.tau*reg
else:
return lossClassify