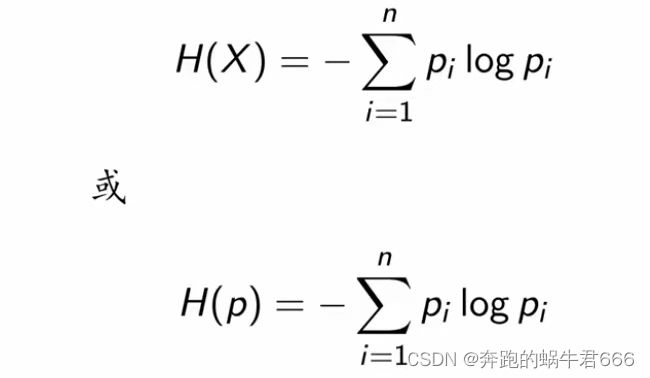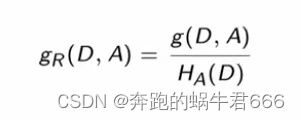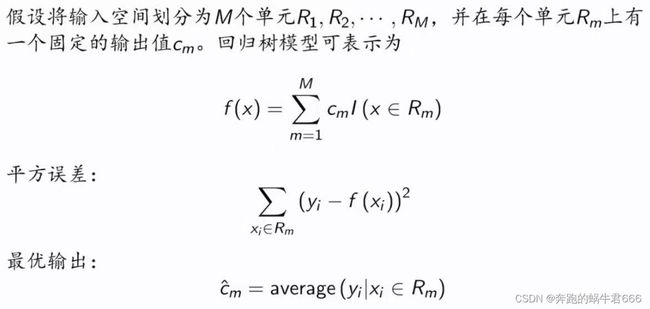统计学习方法 | 决策树

一.一棵有理想的树

分类决策树模型是一种描述对实例进行分类的树形结构

决策树是通过一系列规则对数据进行分类的过程

步骤

①构建根节点

②选择最优特征，以此分割训练数据集

③若子集被基本正确分类，构建叶结点，否则，继续选择新的最优特征

④重复以上两步，直到所有训练数据子集被正确分类

二.条件概率分布

决策树：给定特征条件下类的P(X,Y)

条件概率分布：特征空间的一个划分

划分：单元或区域互不相交

一条路径对应于划分中的一个单元

决策树的条件概率分布由各个单元给定条件下类的条件概率分布组成

三.决策树学习

本质：从训练数据集中归纳出一组分类规则，与训练数据集不相矛盾

假设空间：由无穷多个条件概率模型组成

一棵好的决策树：与训练数据矛盾较小，同时具有很好的泛化能力

策略：最小化损失函数

特征选择：递归选择最优特征

生成：对应特征空间的划分，直到所有训练子集被基本正确分类

剪枝：避免过拟合，具有更好的泛化能力

四.特征选择

1.信息增益：熵 

熵表示的是随机变量的不确定性

随机变量的取值等概率分布的时候，相应的熵最大

0 ≤ H(p) ≤ log n

2.信息增益比 

五.决策树的生成

1.ID3算法

2.C4.5算法

六.剪枝

优秀的决策树：在具有好的拟合和泛化能力的同时，深度小，叶结点少，深度小并且叶结点少

深度：所有结点的最大层次数

误差：训练误差，测试误差

过拟合：训练误差低，测试误差高（模型结构过于复杂）

欠拟合：训练误差高，测试误差低（模型结构过于简单）

剪枝：处理决策树的过拟合问题

预剪枝：生成过程中，对每个结点划分前进行估计，若当前结点的划分不能提升泛化能力，则停止划分，记当前结点为叶结点

后剪枝：生成一棵完整的决策树之后，自底而上地对内部结点变为叶结点，可以提升泛化能力，则做此替换

七.预剪枝

1.限定决策树的深度

2.设定一个阈值

3.设置某个指标，比较结点划分前后的泛化能力

八.后剪枝

降低错误剪枝（REP）：自下而上，使用测试集来剪枝。对每个结点，计算剪枝前和剪枝后的误判个数，若是剪枝有利于减少误判（包括相等的情况），则减掉该结点所在分枝

悲观错误剪枝（PEP）：根据剪枝前后的错误率来决定是否剪枝。和REP不同之处在于，PEP只需要训练集即可，不需要验证集，并且PEP是自上而下剪枝的

最小误差剪枝（MEP）：根据剪枝前后的最小分类错误概率来决定是否剪枝。自下而上剪枝，只需要训练集即可

基于错误剪枝（EBP）：根据剪枝前后的误判个数来决定是否剪枝。自下而上剪枝，只需要训练集即可

后剪枝（CCP）：根据剪枝前后的损失函数来决定是否剪枝

九.CART算法 

分类树 

回归树 

CART树的剪枝

十.Python实现

# 熵
def calc_ent(datasets):
    data_length = len(datasets)
    label_count = {}
    for i in range(data_length):
        label = datasets[i][-1]
        if label not in label_count:
            label_count[label] = 0
        label_count[label] += 1
    ent = -sum([(p / data_length) * log(p / data_length, 2)
                for p in label_count.values()])
    return ent
# def entropy(y):
#     """
#     Entropy of a label sequence
#     """
#     hist = np.bincount(y)
#     ps = hist / np.sum(hist)
#     return -np.sum([p * np.log2(p) for p in ps if p > 0])


# 经验条件熵
def cond_ent(datasets, axis=0):
    data_length = len(datasets)
    feature_sets = {}
    for i in range(data_length):
        feature = datasets[i][axis]
        if feature not in feature_sets:
            feature_sets[feature] = []
        feature_sets[feature].append(datasets[i])
    cond_ent = sum(
        [(len(p) / data_length) * calc_ent(p) for p in feature_sets.values()])
    return cond_ent


# 信息增益
def info_gain(ent, cond_ent):
    return ent - cond_ent


def info_gain_train(datasets):
    count = len(datasets[0]) - 1
    ent = calc_ent(datasets)
#     ent = entropy(datasets)
    best_feature = []
    for c in range(count):
        c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))
        best_feature.append((c, c_info_gain))
        print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain))
    # 比较大小
    best_ = max(best_feature, key=lambda x: x[-1])
    return '特征({})的信息增益最大，选择为根节点特征'.format(labels[best_[0]])

利用ID3算法生成决策树

# 定义节点类 二叉树
class Node:
    def __init__(self, root=True, label=None, feature_name=None, feature=None):
        self.root = root
        self.label = label
        self.feature_name = feature_name
        self.feature = feature
        self.tree = {}
        self.result = {
            'label:': self.label,
            'feature': self.feature,
            'tree': self.tree
        }

    def __repr__(self):
        return '{}'.format(self.result)

    def add_node(self, val, node):
        self.tree[val] = node

    def predict(self, features):
        if self.root is True:
            return self.label
        return self.tree[features[self.feature]].predict(features)


class DTree:
    def __init__(self, epsilon=0.1):
        self.epsilon = epsilon
        self._tree = {}

    # 熵
    @staticmethod
    def calc_ent(datasets):
        data_length = len(datasets)
        label_count = {}
        for i in range(data_length):
            label = datasets[i][-1]
            if label not in label_count:
                label_count[label] = 0
            label_count[label] += 1
        ent = -sum([(p / data_length) * log(p / data_length, 2)
                    for p in label_count.values()])
        return ent

    # 经验条件熵
    def cond_ent(self, datasets, axis=0):
        data_length = len(datasets)
        feature_sets = {}
        for i in range(data_length):
            feature = datasets[i][axis]
            if feature not in feature_sets:
                feature_sets[feature] = []
            feature_sets[feature].append(datasets[i])
        cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)
                        for p in feature_sets.values()])
        return cond_ent

    # 信息增益
    @staticmethod
    def info_gain(ent, cond_ent):
        return ent - cond_ent

    def info_gain_train(self, datasets):
        count = len(datasets[0]) - 1
        ent = self.calc_ent(datasets)
        best_feature = []
        for c in range(count):
            c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))
            best_feature.append((c, c_info_gain))
        # 比较大小
        best_ = max(best_feature, key=lambda x: x[-1])
        return best_

    def train(self, train_data):
        """
        input:数据集D(DataFrame格式)，特征集A，阈值eta
        output:决策树T
        """
        _, y_train, features = train_data.iloc[:, :
                                               -1], train_data.iloc[:,
                                                                    -1], train_data.columns[:
                                                                                            -1]
        # 1,若D中实例属于同一类Ck，则T为单节点树，并将类Ck作为结点的类标记，返回T
        if len(y_train.value_counts()) == 1:
            return Node(root=True, label=y_train.iloc[0])

        # 2, 若A为空，则T为单节点树，将D中实例树最大的类Ck作为该节点的类标记，返回T
        if len(features) == 0:
            return Node(
                root=True,
                label=y_train.value_counts().sort_values(
                    ascending=False).index[0])

        # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征
        max_feature, max_info_gain = self.info_gain_train(np.array(train_data))
        max_feature_name = features[max_feature]

        # 4,Ag的信息增益小于阈值eta,则置T为单节点树，并将D中是实例数最大的类Ck作为该节点的类标记，返回T
        if max_info_gain < self.epsilon:
            return Node(
                root=True,
                label=y_train.value_counts().sort_values(
                    ascending=False).index[0])

        # 5,构建Ag子集
        node_tree = Node(
            root=False, feature_name=max_feature_name, feature=max_feature)

        feature_list = train_data[max_feature_name].value_counts().index
        for f in feature_list:
            sub_train_df = train_data.loc[train_data[max_feature_name] ==
                                          f].drop([max_feature_name], axis=1)

            # 6, 递归生成树
            sub_tree = self.train(sub_train_df)
            node_tree.add_node(f, sub_tree)

        # pprint.pprint(node_tree.tree)
        return node_tree

    def fit(self, train_data):
        self._tree = self.train(train_data)
        return self._tree

    def predict(self, X_test):
        return self._tree.predict(X_test)