【图机器学习】图神经网络入门（一）谱图理论

1 前言

  作为图神经网络的学习基础，谱图理论在图神经网络的基础学习中显得尤为重要，所以准备整理下学习路径。本节的学习基础是之前【理解矩阵系列】和【理解特征值和特征向量】文章。
  这里再谈一下为什么要学习谱图理论。尽管我们经常看到的图神经网络的表达式为 $D^{1/2}A{D}^{1/2}HW$，这是一种空域的形式，但是在查阅图神经网络相关资料或者阅读$Kpif$图神经网络原论文的时候总是绕不开谱域图神经网络这个槛。这是因为图卷积神经网络的核心为卷积操作，而在无规则的图数据结构中，卷积核的定义是十分困难的。因此需要从频谱域(Spectral Domain)上重新定义这样的卷积操作再通过卷积定理转换回空间域上。为了在频谱域和空间域中转换，借助了傅里叶公式，并且定义了图上傅里叶变换(从空间域变换到频谱域)和图上傅里叶逆变换(从频谱域回到空间域)的变换公式。 本节所讲的内容就是图如何在频谱上表示的，即谱图理论！
  内容为自己的学习总结，其中多有借鉴他人的地方，最后一并给出链接。

2 定义

  简单来讲谱图理论研究的是邻接矩阵的性质。严谨来讲谱图理论主要研究的是图的拉普拉斯(Lapalacian)矩阵的特征值和所对应的特征向量对于图拓扑性质的影响，是对图空间拓扑的数学描述。

3 从运动的角度理解特征值和特征向量

  从矩阵变换的角度看，一个向量$x$乘以矩阵$A$，即向量$x$在矩阵$A$给定的方式下进行了运动（变换）。那么这种运动的方式为，在矩阵$A$的特征向量为基的坐标系中，按照矩阵$A$特征值的大小进行了缩放。
  现在我们考虑一个问题，如果一个向量持续地去乘以矩阵$A$会发生什么？我们发现，经过不断的运动变换后的向量会收敛到特征值最大的特征向量上。

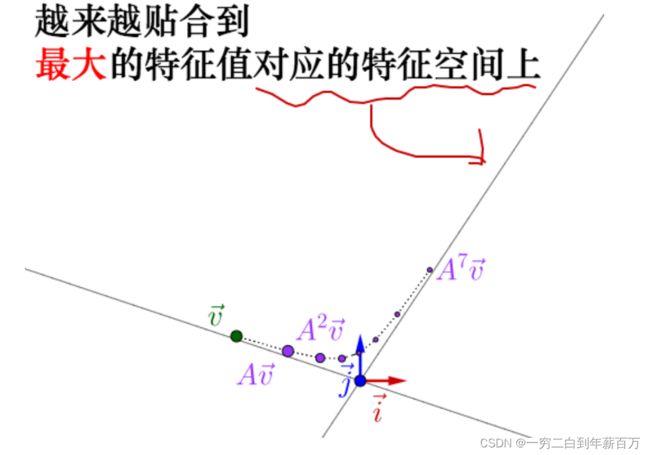
  如果不理解的话可以从计算的角度理解：假设现在有一个$n$维向量$v=[v_1,v_2,......,v_3{]}^T$，我们不停的乘以矩阵$A$。由于向量$v$能够用矩阵$A$的一组特征值$\lambda$和特征向量$u$表示（因为特征向量是相互正交的基，不理解的可以看前言中给出的阅读文章）。所以，
$$v={\alpha }_1{u}_1+{\alpha }_2{u}_2+......+{\alpha }_n{u}_n$$
  由于特征向量的稳定性，不断的乘以矩阵$A$之后，我们发现向量$v$的变化是这样的:
$$\begin{array}{rl}Wv& ={\mu }_1{\alpha }_1{u}_1+{\mu }_2{\alpha }_2{u}_2+\cdots +{\mu }_n{\alpha }_n{u}_n\\ W^{2}v& ={\mu }_1^2{\alpha }_1{u}_1+{\mu }_2^2{\alpha }_2{u}_2+\cdots +{\mu }_n^2{\alpha }_n{u}_n\\ W^{k}v& ={\mu }_1^k{\alpha }_1{u}_1+{\mu }_2^k{\alpha }_2{u}_2+\cdots +{\mu }_n^k{\alpha }_n{u}_n\end{array}$$
  随着$k$趋于无穷，特征值最大的特征向量将会主宰其余的特征向量，从而$v$与特征值最大的$u$变成同一个方向！此外，通过这样的变换，可以观察到$v$的运动过程其实是由各个不同大小的特征值与特征向量控制的。

4 谱图理论

  重点来了，前面讲了这么多又是特征值又是特征向量又是运动等等，这跟图卷积有什么关系？我们之前提到过谱图理论研究的是邻接矩阵，而通过前面的例子我们有点朦朦胧胧的感觉，一个向量$v$不断的乘以一个矩阵$A$，怎么这么像图神经网络的逐层更新公式$D^{1/2}A{D}^{1/2}HW$ ！没错，我们现在研究的对象不是一个矩阵$A$，而是图的邻接矩阵$A$，这样一来知识是不是就串起来了，再深入一点这种连乘然后收敛的性质是不是跟$PageRank$算法很像（此处的内容会在后续文章中慢慢解释，会在此处给出文章链接）。

  回到正题，我们现在的研究对象是图的邻接矩阵。此时，这样的矩阵描述了一种在图上的类似于热力扩散的运动。同样的，该矩阵的特征值刻画了一种运动轨迹，如下图所示（详情见参考文献【5】）。

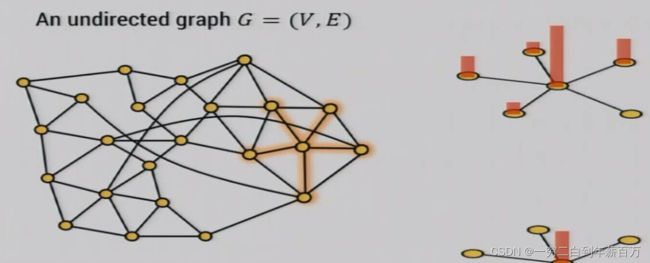
  我们再看一下拉普拉斯矩阵，拉普拉斯矩阵跟谱图理论有什么关系？在以往看到的资料中，凡是涉及到图神经网络的推导，或者谱图卷积总会讲到拉普拉斯矩阵还有它的性质等等。但是并没有讲清楚，为什么需要拉普拉斯矩阵，这就令初学的人很是费解。实际上拉普拉斯矩阵是连接谱域跟空域的桥梁。由于拉普拉斯矩阵是对称矩阵，可以进行特征分解(谱分解)，谱分解对于图从空间域到频谱域的变换至关重要，因为傅里叶变换(Fourier Transform)需要利用Laplacian矩阵的特征值和特征向量，通过变换，从拓扑结构的图(spatial domain)到拉普拉斯矩阵再到谱图(spectral domain)这条链接就形成了。

4.1 拉普拉斯矩阵

  下面就先来介绍拉普拉斯矩阵。
  对于无向图$G=(V,E)$，其Laplacian矩阵定义为$L=D-A$，其中$D$是节点的度矩阵(只在对角线上有元素)，$A$是图的邻接矩阵。拉普拉斯矩阵还有几种扩展定义：

• $L=D^{-1/2}A{D}^{-1/2}$ 称为对称归一化拉普拉斯矩阵(Symmetric Normalized Laplacian)，论文中一般用的是这种Laplacian的定义
• $L=D^{-1}A$称为随机游走归一化拉普拉斯矩阵(Random Walk Normalized Laplacian)

4.2 拉普拉斯矩阵的性质

  矩阵的特征分解，对角化，谱分解都是同一个概念，是指将矩阵分解为由其特征值和特征向量表示的矩阵乘积的方法。只有含有n个线性无关的特征向量的n维方阵才可以进行特征分解。
拉普拉斯矩阵是半正定矩阵，有如下三个性质：

• 是实对称矩阵，有n个线性无关的特征向量

• 这些特征向量都可以正交单位化而得到一组正交且模为 1 的向量

• 所有的特征值非负

  性质1告诉我们拉普拉斯矩阵一定能进行特征分解(谱分解)
$$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^{-1}$$

  由性质2可知，$U$是正交矩阵，即$U{U}^T=I$，故$U^{-1}=U^T$，所以特征分解又可以写成：
$$L=U\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)U^T$$
  性质补充（重要）：【图机器学习入门】拉普拉斯算子与拉普拉斯矩阵的关系

4.3 谱分解

  矩阵的谱分解

5 参考文献

[1]谱图理论(spectral graph theory)
[2]如何理解矩阵特征值和特征向量？
[3]GNN 教程：漫谈谱图理论和GCN的起源
[4]如何理解 Graph Convolutional Network（GCN）？
[5]从物理学角度理解GCN
[6]图的谱图理论