【Pytorch基础教程28】浅谈torch.nn.embedding

学习总结

一、nn.Embedding

CLASStorch.nn.Embedding(num_embeddings, embedding_dim, padding_idx=None, max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False, _weight=None, device=None, dtype=None)[

torch.nn.Embedding经常用来存储单词embedding，使用对应indices进行检索对应的embedding。从上面的官方参数看：

• 输入（最重要的还是前三个参数）：

  • torch.nn.Embedding(
  • num_embeddings, – 词典的大小尺寸，比如总共出现5000个词，那就输入5000。此时index为（0-4999
  • embedding_dim,– 嵌入向量的维度，即用多少维来表示一个符号。
  • padding_idx=None,– 填充id，比如，输入长度为100，但是每次的句子长度并不一样，后面就需要用统一的数字填充，而这里就是指定这个数字，这样，网络在遇到填充id时，就不会计算其与其它符号的相关性。（初始化为0）
  • （不常用）max_norm=None, – 最大范数，如果嵌入向量的范数超过了这个界限，就要进行再归一化。
  • （不常用）norm_type=2.0, – 指定利用什么范数计算，并用于对比max_norm，默认为2范数。
  • scale_grad_by_freq=False, 根据单词在mini-batch中出现的频率，对梯度进行放缩。默认为False.
  • sparse=False, – 若为True,则与权重矩阵相关的梯度转变为稀疏张量。
  • _weight=None)

• 输出：[规整后的句子长度，样本个数（batch_size）,词向量维度]

注：

• 对句子进行规整，即对长度不满足条件的句子进行填充pad（填充的值也可以自己选定），另外句子结尾的EOS也算作一个词。
• 可以通过weight看对应的embedding字典矩阵对应的初始化数值，一般是通过正态分布进行初始化。

二、代码栗子

2.1 通过embedding降维

独热编码向量：维度会太高、向量系数、硬编码。
通过embedding将向量编码为低维、稠密的向量（从data中学习）。

nn.Embedding的shape，注意是会多添加一个embedding_dim维度：

一个1乘4维度矩阵传入10乘3的nn.embedding中，然后得到1乘4乘3矩阵：

# example with padding_idx
embedding = nn.Embedding(10, 3, padding_idx=2)
print(embedding.weight, "\n")

input = torch.LongTensor([[0,2,0,5]])  # 1*4 dim
print(input.shape, "\n")

ans2 = embedding(input)
ans2.shape  # torch.Size([1, 4, 3])

ans2

对应的结果如下，可以看到分别检索出对应的第0,2,0,5行embedding默认的初始权重数据：

Parameter containing:
tensor([[-0.8261,  1.9007,  1.4342],
        [ 1.6798, -0.3864, -1.0726],
        [ 0.0000,  0.0000,  0.0000],
        [-0.9938,  0.3280,  0.1925],
        [-0.2799, -0.9858, -0.7124],
        [ 0.4406,  0.3621, -0.1915],
        [-0.1846,  0.2060, -0.4933],
        [-0.4918,  0.0625, -0.5818],
        [ 0.6995,  0.6223, -1.4094],
        [ 0.3378, -1.0894, -0.7570]], requires_grad=True) 

torch.Size([1, 4]) 

tensor([[[-0.8261,  1.9007,  1.4342],
         [ 0.0000,  0.0000,  0.0000],
         [-0.8261,  1.9007,  1.4342],
         [ 0.4406,  0.3621, -0.1915]]], grad_fn=<EmbeddingBackward0>)

如果input是对应的2乘4矩阵：

# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
from torch.autograd import Variable

# 10个size为3的tensor
# 嵌入字典的大小为10(即有10个词)，每个词向量的维度为3
embedding = nn.Embedding(10, 3)
# a batch of 2 samples of 4 indices each
# 该LongTensor的数字范围只能在0~9(因为设置了10)
input1 = torch.LongTensor([[1, 2, 4, 5], 
                           [4, 3, 2, 9]])
emb1 = embedding(input1) # tensor([[1, 0, 2, 2, 3]])
print(emb1)
print(emb1.shape)
# torch.Size([2, 4, 3]) # 即每个词都被映射为一个3维向量
print('-' * 60)

# 带有padding_idx的栗子
embedding = nn.Embedding(10, 3, padding_idx = 0)
input2 = Variable(torch.LongTensor([[0, 2, 0, 5]]))
emb2 = embedding(input2)
print(emb2)
print(emb2.shape)
# torch.Size([1, 4, 3])

tensor([[[ 0.3004, -0.7126,  0.8605],
         [ 0.1484, -0.9476,  1.0352],
         [ 2.2382, -0.3619, -1.6866],
         [-0.2713,  0.3627,  0.4067]],

        [[ 2.2382, -0.3619, -1.6866],
         [ 1.2409,  0.6028,  0.0371],
         [ 0.1484, -0.9476,  1.0352],
         [-0.5018,  0.3566, -0.6405]]], grad_fn=<EmbeddingBackward>)
torch.Size([2, 4, 3])
------------------------------------------------------------
tensor([[[ 0.0000,  0.0000,  0.0000],
         [ 2.4998,  0.4584,  0.0595],
         [ 0.0000,  0.0000,  0.0000],
         [ 1.0930, -1.0224,  0.8367]]], grad_fn=<EmbeddingBackward>)
torch.Size([1, 4, 3])

2.2 RNN中用embedding改进

# -*- coding: utf-8 -*-
import torch 
import torch.nn as nn
import matplotlib.pyplot as plt

num_class = 4
input_size = 4
hidden_size = 8
embedding_size = 10
num_layers = 2
batch_size = 1
seq_len = 5

# 准备数据
idx2char = ['e', 'h', 'l', 'o']
# (batch, seq_len)
x_data = [[1, 0, 2, 2, 3]]
# (batch * seq_len)
y_data = [3, 1, 2, 3, 2]

one_hot_lookup = [[1, 0, 0, 0],
                  [0, 1, 0, 0],
                  [0, 0, 1, 0],
                  [0, 0, 0, 1]]

# inputs 作为交叉熵中的Inputs,维度为(batchsize, Seqlen)
inputs = torch.LongTensor(x_data)
# labels 作为交叉熵中的target,维度为(batchsize, Seqlen)
labels = torch.LongTensor(y_data)
losslst = []


# 模型设计
class Model(nn.Module):
    def __init__(self, input_size, hidden_size, batch_size):
        super(Model, self).__init__()
        # 字典大小为input_size,映射后的词向量大小为embedding_size
        self.emb = torch.nn.Embedding(input_size, embedding_size)
        self.rnn = torch.nn.RNN(input_size = embedding_size,
                                hidden_size = hidden_size,
                                num_layers = num_layers,
                                batch_first = True)
        # 增加线性层使得在处理输入输出维度不同时更加稳定
        self.fc = nn.Linear(hidden_size, num_class)
        
    def forward(self, x):
        hidden = torch.zeros(num_layers, x.size(0), hidden_size)
        # (batch, seqLen, embeddingSize)
        x = self.emb(x)
        x, _ = self.rnn(x, hidden)
        x = self.fc(x)
        return x.view(-1, num_class)
    
    
net = Model(input_size,
            hidden_size,
            batch_size)

# loss函数和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(),
                             lr = 0.05)


for epoch in range(15):
    optimizer.zero_grad()
    outputs = net(inputs)
    # labels的shape是seq×B×1
    # outputs的shape是seq×B×H
    loss = criterion(outputs, labels)
    losslst.append(loss.item())
    
    loss.backward()
    optimizer.step()
    
    _, idx = outputs.max(dim = 1)
    idx = idx.data.numpy()
    print('Predicted:', ''.join([idx2char[x] for x in idx]), end = '')
    print(', Epoch [%d/15] loss = %.3f' % (epoch + 1, loss.item()))
    
    
plt.plot(range(15), losslst)
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.show()

这次可以看到第6个epoch就收敛到ohlol了，如果没用embedding则是第8个epoch才收敛到这个单词。

Predicted: oeeol, Epoch [1/15] loss = 1.371
Predicted: ollll, Epoch [2/15] loss = 1.122
Predicted: ollll, Epoch [3/15] loss = 0.980
Predicted: ollll, Epoch [4/15] loss = 0.849
Predicted: ohlll, Epoch [5/15] loss = 0.703
Predicted: ohlol, Epoch [6/15] loss = 0.543
Predicted: ohlol, Epoch [7/15] loss = 0.386
Predicted: ohlol, Epoch [8/15] loss = 0.269
Predicted: ohlol, Epoch [9/15] loss = 0.180
Predicted: ohlol, Epoch [10/15] loss = 0.113
Predicted: ohlol, Epoch [11/15] loss = 0.075
Predicted: ohlol, Epoch [12/15] loss = 0.051
Predicted: ohlol, Epoch [13/15] loss = 0.036
Predicted: ohlol, Epoch [14/15] loss = 0.026
Predicted: ohlol, Epoch [15/15] loss = 0.019

再比如在NLP最基础的word2vec模型中，我们需要把词向量从word2vec模型中提取出来，而每个词对应的embedding其实就藏在输入层到隐层的的权重矩阵中。如下图中的橙色部分：Embedding Matrix。

输入向量矩阵 $W_{V\times N}$ 的每一个行向量对应的就是我们要找的“词向量”（即上图中橙色矩阵中的每行深色橙色向量）。

比如我们要找词典里第 i 个词对应的 Embedding，因为输入向量是采用 One-hot 编码的，所以输入向量的第 i 维就应该是 1，那么输入向量矩阵 $W_{V\times N}$ 中第 i 行的行向量自然就是该词的 Embedding 。

• 注1：输出向量矩阵 W′ 也遵循这个道理，确实是这样的，但一般来说，我们还是习惯于使用输入向量矩阵（即这里的$W_{V\times N}$）作为词向量矩阵。

$W_{V\times N}$权重矩阵，下角标是（VxN），也就是输入层和隐藏层的权重矩阵，如果看一下维度的话，比如输入是一个10000维的词的one-hot编码，那么这里的V就是10000，我们的输入应该是VxN的，那么我们的隐藏层有N个神经元，那么我们的权重矩阵不就是VxN的咯？而我们在python代码里运行torch.nn.Embedding()时候，第一个参数是输入维度，第二个参数是隐藏层维度，所以也就是说 我们习惯取这样的输入和隐藏层之间的权重矩阵为我们的Embedding矩阵。

• 注2：一般我们会把输入向量矩阵转为词向量查找表（lookup table），如输入向量是 10000 个词组成的 One-hot 向量，隐层维度是 300 维，那么输入层到隐层的权重矩阵为 10000x300 维。在转换为词向量 Lookup table 后，每行的权重即成了对应词的 Embedding 向量。如果我们把这个查找表存储到线上的数据库中，就可以轻松地在推荐物品的过程中使用 Embedding 去计算相似性等重要的特征了。

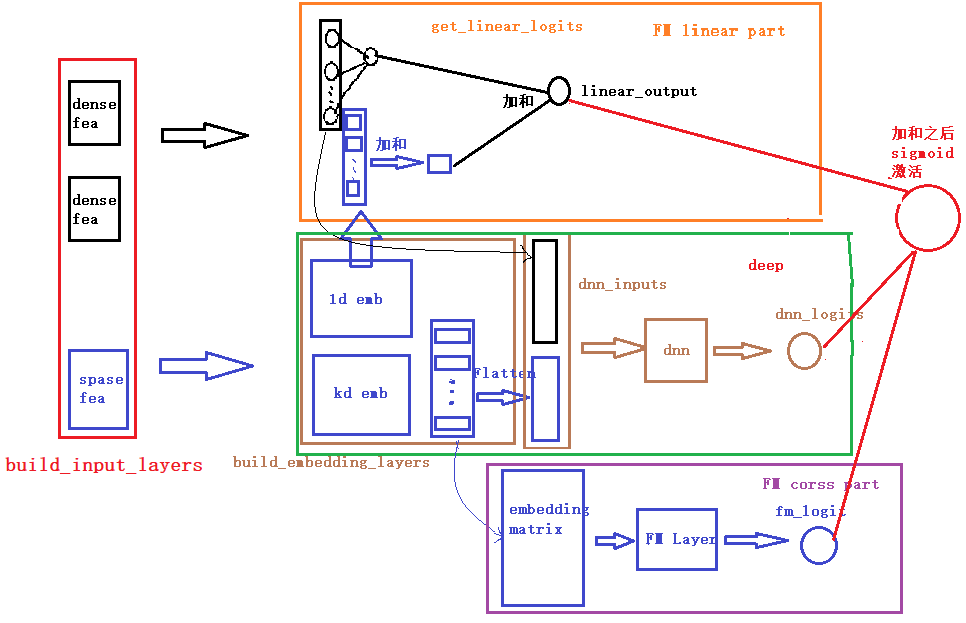
2.3 deepFM模型中embedding

• deep_features指用deep模块训练的特征（兼容dense和sparse）
• fm_features指用fm模块训练的特征，只能传入sparse类型

class MyDeepFM(torch.nn.Module):
  # Deep和FM为两部分，分别处理不同的特征，因此传入的参数要有两种特征，由此我们得到参数deep_features,fm_features
  # 此外神经网络类的模型中，基本组成原件为MLP多层感知机，多层感知机的参数也需要传进来，即为mlp_params
  def __init__(self, deep_features, fm_features, mlp_params):
    super().__init__()
    self.deep_features = deep_features
    self.fm_features = fm_features
    self.deep_dims = sum([fea.embed_dim for fea in deep_features])
    self.fm_dims = sum([fea.embed_dim for fea in fm_features])
    # LR建模一阶特征交互
    self.linear = LR(self.fm_dims)
    # FM建模二阶特征交互
    self.fm = FM(reduce_sum=True)
    # 对特征做嵌入表征
    self.embedding = EmbeddingLayer(deep_features + fm_features)
    self.mlp = MLP(self.deep_dims, **mlp_params)

  def forward(self, x):
    input_deep = self.embedding(x, self.deep_features, squeeze_dim=True)  #[batch_size, deep_dims]
    input_fm = self.embedding(x, self.fm_features, squeeze_dim=False)  #[batch_size, num_fields, embed_dim]

    y_linear = self.linear(input_fm.flatten(start_dim=1))
    y_fm = self.fm(input_fm)
    y_deep = self.mlp(input_deep)  #[batch_size, 1]
    # 最终的预测值为一阶特征交互，二阶特征交互，以及深层模型的组合
    y = y_linear + y_fm + y_deep
    # 利用sigmoid来将预测得分规整到0,1区间内
    return torch.sigmoid(y.squeeze(1))

• 看项目源码可知这里的fm的返回值是二阶特征交叉部分，y_linear是一阶特征交叉部分（用LR进行建模了）
• 这里的self.embedding层也很常见，和torch.nn.embedding功能类似，传入对应的feature_name列表等几个参数，然后返回对应特征的embedding。对应详细的embedding层代码也可以参考：https://github.com/datawhalechina/torch-rechub/blob/main/torch_rechub/basic/layers.py。

Reference

[1] https://pytorch.org/docs/stable/generated/torch.nn.Embedding.html?highlight=embedding#torch.nn.Embedding