FixMatch：一致性正则与伪标签

FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence

• Google research出品

• 论文：https://arxiv.org/abs/2001.07685

• 官方代码：https://github.com/google-research/fixmatch

---

摘要

• FixMatch是SSL的两种方法的组合：一致性正则和伪标签

对于无标签的样本，FixMatch：

• FixMatch首先对弱增强的无标签图像，预测伪标签
  • 对于给定的图像，只有当模型产生高于阈值的预测时，才会保留作为伪标签
• 再对同一图像的强增强版本，预测出分类概率
  • 通过交叉熵损失衡量，强弱二者的预测的一致性

FixMatch的核心：

• 一致性正则和伪标签方法的，简单组合
• 无标签模型预测，与UDA一样，采用RandAugment[3]进行强增强

主要贡献：（A+B=C的操作）

主要结合了pseudo label 和 consistency regularization两种数据增强方式实现方法。

---

FixMatch的流程

• 首先，利用一张无标签样本，分别进行：
  • “弱”增强（翻转、缩放）
  • “强”增强（CutOut、CTAugment、RandAugment),
• 然后，通过model得到预测标签
• 并，通过标准交叉熵损失计算损失
• 注意：
  • 上述**“弱“增强方式预测过程，需要设定一个阈值**
  • 大于阈值的才计算loss，小于的就不计算
  • 相当于，在前期训练阶段中，无标签样本损失可能一直是为0的

首先，将未标记图像的弱增强版本（顶部）输入模型中以获得其预测（红色框）。

当模型为高于阈值（虚线）的任何类别分配概率时，预测将转换为单伪标记。

然后，针对同一张图片的增强版本（底部）计算模型的预测。

训练该模型，使其通过标准的交叉熵损失，使其在强增强版本上的预测与伪标记匹配。

---

一致性正则 、伪标签

1. 一致性正则的思想：

即使在无标签的样本被注入噪声之后，分类器也应该为其输出相同的类分布概率。即强制一个无标签的样本，应该被分类为与自身的增强 相同的分类

2. 伪标签：

• 使用模型本身为无标签数据，获取标签的方法。
  • 具体而言，将模型输出的softmax概率分布视为软伪标签；
  • 或将经过argmax或者one_hot得到的预测视为硬伪标签。
• 利用这些伪标签，作为监督损失进一步训练模型。

---

损失的Background

一致性正则化

• 利用未标记的数据，基于这样的假设，即当输入受到扰动的图像时，模型应该输出相似的预测。

• 模型通过标准监督分类损失，和以下损失函数对未标记数据进行训练：

  ${\sum }_{b=1}^{\mu B}\Vert p_m(y|\alpha (u_b))-p_m(y|\alpha (u_b)){\Vert }_2^2$

伪标记

• 我们应该使用模型本身，来为未标记的数据，获取人工标记
• 伪标签，特别指使用**“硬”标签**
  • 即只保留人工标签，其最大类概率落在预定义的阈值之上
• 假设 $q_b=p_m(y|\mu )$ ，伪标记对未标记数据使用以下损失函数:

$\frac{1}{\mu B}{\sum }_{b=1}^{\mu B}1(\max (q_b)\ge \tau )H({\hat{q}}_b,q_b)$

• 假设，应用于概率分布的arg max，生成一个有效的**“onehot”概率分布**
• 硬标签的使用，使得伪标签与熵最小化，密切相关
• 其中模型的预测，被鼓励为低熵(即未标记的数据)

---

FixMatch的损失函数

由两个交叉熵损失项组成：

1. 一个是应用于，有标签数据的，全监督损失
2. 另一个是用于，无标签数据的，一致性正则损失。

损失函数由两个交叉熵损失项组成：一个监督损失项 $l_S$， 一个无监督损失项$l_U$

$X=\{(x_b,p_b):b\in (1,\dots ,B)\}$

• $ x _ { b } $ 是训练样本
• $p_b$ 是one-hot编码
• $B$ 是BatchSIze

$U=\{u_b:b\in (1,\dots ,\mu B)\}$ 表示一个Batch的未标记样本

• $\mu$ 是决定$X$ 和 $U$ 的数量关系的超参数，表示$X$ 和 $U$ 的相对大小

$p_m(y|x)$ 表示模型对输入$x$ 预测的类别分布

将两个概率分布，$p$ 和 $q$ 之间的交叉熵表示为 $H(q,p)$

两种类型的增强: 强增强$A(\cdot )$ ; 弱增强表示为 $\alpha (\cdot )$

====>

• 对于有标签样本，FixMatch均采用弱增强，其损失函数为：

  ${\ell }_s=\frac{1}{B}{\sum }_{b=1}^{B}H(p_b,p_m(y|\alpha (x_b)))$

  """
  将有 / 无标签的 batch 拼接后输入模型
  
  :inputs_x: 有标签数据
  :inputs_u_w: 无标签数据的弱增强
  :inputs_u_s: 无标签数据的强增强
  """
  inputs = interleave(
      paddle.concat((inputs_x, inputs_u_w, inputs_u_s)), 2 * args.mu + 1)
  # 模型输出（全连接层分类预测）
  logits = model(inputs)
  logits = de_interleave(logits, 2 * args.mu + 1)
  # 有标签数据的模型输出
  logits_x = logits[:batch_size]
  
  # 有标签预测的交叉熵损失
  Lx = F.cross_entropy(logits_x, targets_x, reduction='mean')
  

• 对于无标签样本，FixMatch为每个无标签样本预测一个伪标签，然后用于计算交叉熵损失。

  • 为了获得一个伪标签，首先输入无标签图像的弱增强版本 ，并得到模型预测的类概率分布： $q_b=p_m(y|\alpha ({\mu }_b))$

  • 然后，使用 ${\hat{q}}_b=\mathrm{argmax}(q_b)$ ，得到硬伪标签；

  • 接着与 ${\mu }_b$ 的强增强版本 得到的模型预测，计算一致性正则损失：

    ${\ell }_u=\frac{1}{\mu B}{\sum }_{b=1}^{\mu B}1(\max (q_b)\ge \tau )H({\hat{q}}_b,p_m(y|A(u_b)))$

    • 其中， τ 是一个标量超参数，是用于筛选伪标签的阈值，
    • 超过该阈值，才将该伪标签纳入损失计算。

 # 弱增强和强增强模型预测
logits_u_w, logits_u_s = logits[batch_size:].chunk(2)

# 对弱增强的模型输出使用 softmax + argmax 得到伪标签 targets_u
pseudo_label = F.softmax(logits_u_w.detach() / args.T, axis=-1)
targets_u = paddle.argmax(pseudo_label, axis=-1)  # 利用 argmax 得到硬伪标签
# 通过阈值筛选伪标签
max_probs = paddle.max(pseudo_label, axis=-1)
mask = paddle.greater_equal(
               max_probs, 
               paddle.to_tensor(args.threshold)).astype(paddle.float32)
# 无标签预测的交叉熵损失（一致性损失）
Lu = (F.cross_entropy(logits_u_s, targets_u,
                      reduction='none') * mask).mean()
# 两个损失加权相加
loss = Lx + args.lambda_u * Lu

• FixMatch的总损失

  总损失是两个损失函数的加权和：

  $l_s+{\lambda }_u{l}_u$

  • 其中 λ 表示无标签损失的权重，官方开源代码中其设为1。

---

FixMatch算法过程

---

Augmentation in FixMatch

FixMatch利用两种增强: “弱”和“强

• 弱增强。是标准的翻转-移位增强策略

  • 在水平方向上，随机翻转图像，概率为50%

  • 在垂直和水平方向上，随机转换图像，概率最高为12.5%

• “强”增强。尝试了两种基于自增强的方法

  • AutoAugment
    • 使用强化学习
    • 从Python图像库，学习基于转换的增强策略
  • 人们提出了自动增强的变体，它不需要使用标记数据提前学习增强策略
  • Rand-Augment[10] 和 CT-Augment[2]
    • 给定一组变换（例如颜色反转、平移、对比度调整等），Rand-Augment随机选择小批量中每个样本的变换
    • CTAugment[2]没有随机设置转换量，而是在训练过程中在线学习

---

FixMatch的简洁之处

FixMatch和其他的SSL方法的关键区别在于

• 伪标签是基于弱增强图像预测的硬伪标签

• 而对于强增强图像的模型输出的全连接层预测，直接计算损失（不进行 argmax）

• 这对FixMatch的成功至关重要

• UDA和MixMatch中用了sharpen构建软伪标签

• sharpen 引入了一个超参数

• 但 并不是起到筛选伪标签的作用

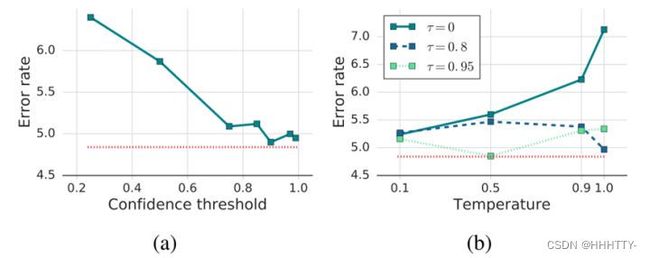
  FixMatch 的消融实验表明

  • 阈值 τ 控制伪标签的质量和数量之间的平衡
  • 无标签数据的伪标签的准确性，随着 τ 的增加而增加（下图（a）， τ 时达到最佳）
  • 将参数 （Temperature）引入FixMatch，非但不会获得更好的性能（下图（b）），还会增加调参成本

在Mean-Teacher、MixMatch等SSL算法中

• 在训练期间，会增加无标签损失项的权重（ λ ）
• 实验表明，这对于FixMatch来说是不必要的
  • 这可能是因为在训练早期 通常小于 τ
  • 随着训练的进行，模型的预测变得更加自信
  • 大于 τ 的情况更常见
    • 这表明：伪标签促进了网络的学习进步
    • 而且获取伪标签是“免费的”

---

FixMatch的“强弱调和”

FixMatch利用了两种数据增强：“弱”和“强”

• 弱增强是标准的随机翻转和移位的数据增强策略。

• 对于弱增强，FIxMatch在有标签数据样本上以50%的概率进行水平翻转图像；

  • 以12.5%的概率在垂直和水平方向上随机平移图像；

• 对于强增强，FixMatch与UDA一样

  • 利用了RandAugment为每个无标签样本随机选择变换

论文还研究了，弱增强和强增强的不同组合对伪标签生成的影响：

• 当将预测伪标签的弱增强替换为强增强时，实验发现模型在训练早期就出现了分歧；
• 相反，当用无增强替换弱增强时，该模型会过度拟合无标签数据；
• 使用弱增强代替原先的强增强时，只能达到45%的准确率峰值，但不稳定，并逐渐下降到12%，表明了强增强的重要性。

---

FixMatch的优化器

• FixMatch使用weight decay模型参数正则化
• 论文做了消融实验，相较于使用Momentum优化器，使用Adam优化器会导致更差的性能
• 对于Momentum优化器参数的设置，momentum=0.9，weight_decay=0.0005，use_nesterov=True。

由于优化器采用了weight_decay

• 需要剔除：设置了bias=True参数的网络层和BatchNorm层

no_decay = ['bias', 'bn']
scheduler = get_cosine_schedule_with_warmup(args.lr, args.warmup, args.total_steps)

grouped_parameters = [
    # 若网络层不包含 bias 或 BatchNorm，则应用 weight_decay
    {'params': [p for n, p in model.named_parameters() if not any(
        nd in n for nd in no_decay)], 'weight_decay': args.wdecay},
    # 反之，则不用 weight_decay
    {'params': [p for n, p in model.named_parameters() if any(
        nd in n for nd in no_decay)], 'weight_decay': 0.0}
]

optimizer = optim.Momentum(learning_rate=scheduler,
                           momentum=0.9,
                           parameters=grouped_parameters,
                           use_nesterov=args.nesterov)

余弦学习率衰减

使用余弦学习速率衰减，衰减策略设置为

$\eta \cos (\frac{7\pi k}{16K})$ ，其中 η 是初始学习率

def get_cosine_schedule_with_warmup(learning_rate, num_warmup_steps,
                                    num_training_steps,
                                    num_cycles=7. / 16.,
                                    last_epoch=-1):
    """
    借助 LambdaDecay 实现余弦学习率衰减
    """
    def _lr_lambda(current_step):
        if current_step < num_warmup_steps:
            return float(current_step) / float(max(1, num_warmup_steps))
        no_progress = float(current_step - num_warmup_steps) / \
                      float(max(1, num_training_steps - num_warmup_steps))
        return max(0., math.cos(math.pi * num_cycles * no_progress))

    return LambdaDecay(learning_rate=learning_rate,
                       lr_lambda=_lr_lambda,
                       last_epoch=last_epoch)

---

模型训练

backbone网络架构：默认为 Wide ResNet-28-2

训练的超参数如下：

• 无标签损失权重 λ

• 初始学习率 η

• 优化器 momentum 参数 β ，weight_decay 参数 λ

• 伪标签阈值 τ

• 有 / 无标签样本比例 1: 7： μ

• batch_size

---

实验

尽管FixMatch非常简单，但它在各种标准的半监督学习benchmark上都达到了SOTA

• 在CIFAR-10[5]上，仅有250个标签时，准确率为94.93%
• 在40个标签时，准确率为88.61%（每类仅4个标签）

为了得到最优超参数，该文章后面对超参做了大量的消融实验

• 比如学习率，衰减率、学习率衰减函数
• 标签样本与无标签样本比例、动量、优化器选择
• 伪标签中用的阈值，包括sharpen中的τ

---

结论

在半监督学习算法日益复杂的发展中，FixMatch以出人意料的简单获得了SOTA性能

• 在有标签和无标签的数据上，只使用标准的交叉熵损失
• FixMatch的训练，只需几行代码即可完成。

论文指出，由于这种简单性，我们能够彻底研究FixMatch是如何发挥作用的

• 我们发现某些设计选择很重要（而且往往被低估）——最重要的是weight decay和优化器的选择。
• 总的来说，我们相信，这种简单但性能良好的半监督机器学习算法的存在
  • 将有助于机器学习被应用到越来越多的标签价格昂贵或难以获得的实际领域