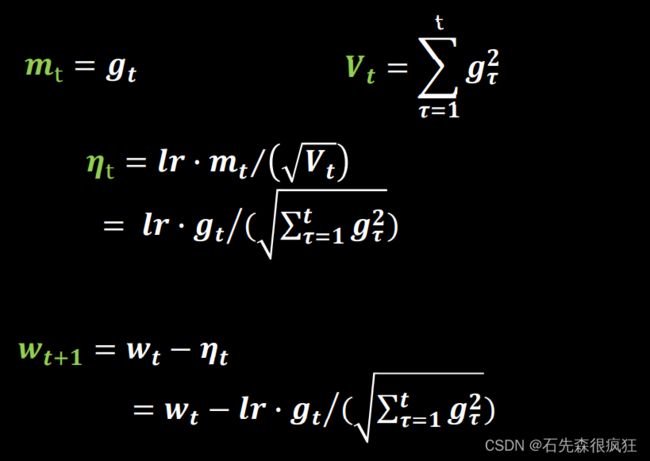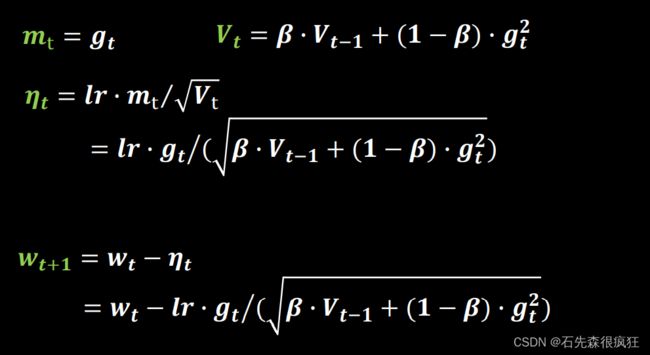TensorFlow2.0笔记(北京大学)不断更新
TensorFlow2.0
北京大学TensorFlow2.0笔记文章目录
- TensorFlow2.0
- 前言
- 一、人工智能三学派
- 二、基于连接主义的神经网络设计过程
- 三、Tensor张量
-
- 1、tf.constant()
- 2、将numpy的数据类型转换为Tensor数据
- 3、创建张量
- 4、生成随机数
- 四、TensorFlow常用函数
-
- 1、计算张量维度的最大最小值与强制转换tensor数据类型
- 2、计算指定维度
- 3、张量的四则运算
- 4、张量的方运算
- 5、张量的矩阵运算
- 6、切分传入张量的第一维度,生成输入特征/标签对,构建数据集
- 7、python中遍历每个元素
- 8、tf.one_hot独热编码(常用独热编码做标签)
- 9、使输出符合概率的分布
- 10、赋值操作,更新参数的值并返回
- 11、返回张量沿指定维度最大值的索引
- 四、鸢尾花的分类
-
- 神经网络实现鸢尾花的分类流程:
- 1.从sklearn包datasets读入数据集
- 2.神经网络实现鸢尾花的分类
- 五、预备知识
-
- 1、tf.where(条件语句, 真返回A, 假返回B)
- 2、np.random.RandomState.rand(维度)
- 3、np.vstack((数组1, 数组2))将两个数据按垂直方向叠加
- 4、np.mgrid[ ]、 x.ravel()、np.c_[ ]
- 六、复杂度学习率
-
- 1、学习率公式:
- 2、 如何寻找最优学习率?
- 七、激活函数
-
- 1、Sigmoid函数
- 2、Tanh函数
- 3、Relu函数
- 4、Leaky Relu函数
- 5、softmax函数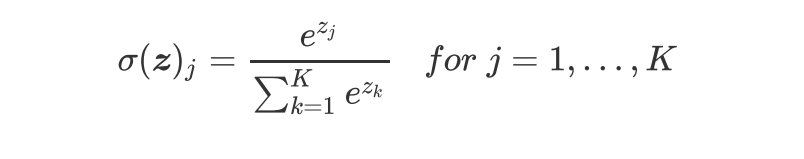
- 6、选择函数建议
- 八、损失函数
-
- 1、均方误差损失函数
- 2、自定义损失函数
- 3、交叉熵损失函数
- 九、欠拟合与过拟合
-
- 正则化缓解过拟合
- 正则化的选择
- 十、优化器
-
- 1.SGD随机梯度下降
- 2.SGDM
- 3.Adagrad,在SGD基础上增加二阶动量
- 4.RMSProp,SGD基础上增加二阶动量
- 5.Adam, 同时结合SGDM一阶动量和RMSProp二阶动量
- 十一、搭建网络八股
- 总结
前言
- TensorFlow
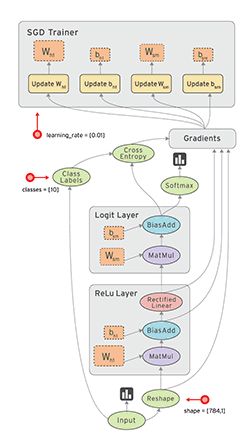
是一个采用数据流图(Data Flow Graphs),用于高性能数值计算的开源软件库。 - Tensor(张量)
即多维数组,是TensorFlow中数据表现的形式。Flow:基于数据流图(Data FlowGraphs)的计算。 - Data Flow
Graph用结点和线的有向图来描述数学计算。节点通常代表数学运算,边表示节点之间的某种联系,它负责传输多维数据(Tensors)。如下图所示:
提示:以下是本篇文章正文内容,下面案例可供参考
一、人工智能三学派
- 行为主义:
基于控制论,构建感知-动作控制系统。如人的平衡、行走、避障等自适应控制系统 - 符号主义:
基于算数逻辑表达式,求解问题时先把问题描述为表达式,再求解表达式。可用公式描述、实现理性思维,如专家系统。 - 连接主义:
仿生学,模仿神经元连接关系。仿脑神经元连接,实现感性席位,如神经网络
二、基于连接主义的神经网络设计过程
- 准备数据:采集大量“特征/标签”数据
- 搭建网络:搭建神经网络结构
- 优化参数:训练网络获取最佳参数
- 应用网络:将网络保存为模型,输入新数据,输出分类或者预测结果
三、Tensor张量
1、tf.constant()
- 用法:tf.constant(“内容”)
# 第一个tensorflow程序
import tensorflow.compat.v1 as tf
# 要打印一个常量字符串用 tf.constant创建一个张量
c = tf.constant("Hello World")
# 直接打印c,会输出张量的所有信息
print(c)
# 打印张量的类型
print(c.dtype)
# 打印张量的内容
print(c.shape)
3 # 这个 0 阶张量就是标量,shape=[]
[1., 2., 3.] # 这个 1 阶张量就是向量,shape=[3]
[[1., 2., 3.], [4., 5., 6.]] # 这个 2 阶张量就是二维数组,shape=[2, 3]
[[[1., 2., 3.]], [[7., 8., 9.]]] # 这个 3 阶张量就是三维数组,shape=[2, 1, 3]
- dtype Tensor 存储的数据的类型,可以为tf.float32、tf.int32、tf.string…
- shape Tensor 存储的多维数组中每个维度的数组中元素的个数
应用实例:
# 引入 tensorflow 模块
import tensorflow as tf
# 创建一个整型常量,即 0 阶 Tensor
t0 = tf.constant(3, dtype=tf.int32)
# 创建一个浮点数的一维数组,即 1 阶 Tensor
t1 = tf.constant([3., 4.1, 5.2], dtype=tf.float32)
# 创建一个字符串的2x2数组,即 2 阶 Tensor
t2 = tf.constant([['Apple', 'Orange'], ['Potato', 'Tomato']], dtype=tf.string)
# 创建一个 2x3x1 数组,即 3 阶张量,数据类型默认为整型
t3 = tf.constant([[[5], [6], [7]], [[4], [3], [2]]])
很多时候数据是由numpy格式给出的
因此要将numpy的数据类型转换为Tensor数据类型
2、将numpy的数据类型转换为Tensor数据
- 用法:tf.convert_to_tensor(数据名, dtype=数据类型)
应用实例:
import tensorflow as tf
import numpy as np
# 创建一个0-4的数
a = np.arange(0, 5)
# 将numpy的数据类型转换为Tensor数据类型
b = tf.convert_to_tensor(a, dtype=tf.int64)
3、创建张量
import tensorflow as tf
# 维度:
# 一维直接写个数
# 二维用[行, 列]
# 多维用[n,m,j,k...]
# 创建全为0的张量 tf.zeros(维度)
a = tf.zeros([2, 3])
# 创建全为1的张量 tf.ones(维度)
b = tf.ones(4)
# 创建全为指定值的张量 tf.fill(维度, 指定值)
c = tf.fill([2, 2], 9)
print("a:", a)
print("b:", b)
print("c:", c)
4、生成随机数
import tensorflow as tf
# 生成正态分布的随机数,默认均值为0,标准差为1
# tf.random.normal(维度, mean=均值, stddev=标准差)
d = tf.random.normal([2, 2], mean=0.5, stddev=1)
print("d:", d)
# 生成截断式正太分布的随机数
# tf.random.truncated_normal(维度, mean=均值, stddev=标准差)
e = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)
print("e:", e)
# 生成均匀分布随机数
# tf.random.uniform(维度, minval=最小值, maxval=最大值)
f = tf.random.uniform([2, 2], minval=0, maxval=1)
print("f:", f)
注意区间: [minval=最小值, maxval=最大值) 前开后闭
四、TensorFlow常用函数
1、计算张量维度的最大最小值与强制转换tensor数据类型
# 常用函数
import tensorflow as tf
x1 = tf.constant([1., 2., 3.], dtype=tf.float64)
print("x1:", x1)
# 强制tensor转换为该数据类型
# tf.cast(张量名, 数据类型)
x2 = tf.cast(x1, tf.int32)
print("x2", x2)
# tf.reduce_min(张量名) 计算张量维度上元素的最小值
print("minimum of x2:", tf.reduce_min(x2))
# tf.reduce_max(张量名) 计算张量维度上元素的最大值
print("maxmum of x2:", tf.reduce_max(x2))
2、计算指定维度
import tensorflow as tf
# axis=1代表跨列,沿纬度方向(横)
# axis=0代表跨行,沿经度方向(竖)
x = tf.constant([[1, 2, 3], [2, 2, 3]])
print("x:", x)
# 计算沿指定维度的平均值 tf.reduce_mean(张量名)
# 如果不指定axis,则所有元素参与计算
print("mean of x:", tf.reduce_mean(x)) # 求x中所有数的均值
# 计算沿指定维度的和 tf.reduce_sum(张量名, axis=操作轴)
print("sum of x:", tf.reduce_sum(x, axis=1)) # 求每一行的和
- axis=1代表跨列,沿纬度方向(横)
- axis=0代表跨行,沿经度方向(竖)
3、张量的四则运算
import tensorflow as tf
a = tf.ones([1, 3])
b = tf.fill([1, 3], 3.)
print("a:", a)
print("b:", b)
# 实现两个张量的对应元素相加
print("a+b:", tf.add(a, b))
# 实现两个张量的对应元素相减
print("a-b:", tf.subtract(a, b))
# 实现两个张量的对应元素相乘
print("a*b:", tf.multiply(a, b))
# 实现两个张量的对应元素相除
print("b/a:", tf.divide(b, a))
# 注意只有维度相同的张量才可以做四则运算
4、张量的方运算
a = tf.fill([1, 2], 3.)
print("a:", a)
# 计算某个张量的n次方
print("a的平方:", tf.pow(a, 3))
# 计算某个张量的平方
print("a的平方:", tf.square(a))
# 计算某个张量的开方
print("a的开方:", tf.sqrt(a))
5、张量的矩阵运算
import tensorflow as tf
a = tf.ones([3, 2])
b = tf.fill([2, 3], 3.)
print("a:", a)
print("b:", b)
# 实现两个矩阵的相乘
print("a*b:", tf.matmul(a, b))
6、切分传入张量的第一维度,生成输入特征/标签对,构建数据集
import tensorflow as tf
features = tf.constant([12, 23, 10, 17])
labels = tf.constant([0, 1, 1, 0])
# 切分传入张量的第一维度,生成输入特征/标签对,构建数据集
# dataset = tf.data.Dataset.from_tensor_slices((输入特征, 标签))
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
for element in dataset:
print(element)
# Numpy和Tensor格式都可以使用该语句读入数据
7、python中遍历每个元素
seq = ['one', 'two', 'three']
# enumerate是python内建函数,可以遍历每个元素
# 组合为:索引 元素,常在for循环使用
# element(列表名)
for i, element in enumerate(seq):
print(i, element)
8、tf.one_hot独热编码(常用独热编码做标签)
import tensorflow as tf
# tf.one_hot独热编码
# 在分类问题中,常用独热编码做标签,标记类别:1表示是,0表示非
# tf.one_hot()函数将待转换数据,转换为one-hot形式的数据输出
# tf.one_hot(待转换数据, depth=分几类)
classes = 3
labels = tf.constant([1, 0, 2]) # 输入的元素值最小为0,最大为2
output = tf.one_hot(labels, depth=classes)
print("result of labels1:", output)
print("\n")
9、使输出符合概率的分布
import tensorflow as tf
# 当n分类的n个输出,(y0,y1,...yn-1)通过softmax()函数,便符合概率分布了
# tf.nn.softmax() 使输出符合概率的分布
y = tf.constant([1.01, 2.01, -0.66])
y_pro = tf.nn.softmax(y)
print("After softmax, y_pro is:", y_pro) # y_pro 符合概率分布
print("The sum of y_pro:", tf.reduce_sum(y_pro)) # 通过softmax后,所有概率加起来和为1
10、赋值操作,更新参数的值并返回
import tensorflow as tf
# 赋值操作,更新参数的值并返回
# 调用assign_sub前,先用tf.Variable定义变量为可训练
# assign_sub(要自减的内容)
x = tf.Variable(4)
x.assign_sub(1)
print("x:", x) # 4-1=3
11、返回张量沿指定维度最大值的索引
import numpy as np
import tensorflow as tf
# 返回张量沿指定维度最大值的索引
# tf.argmax(张量名, axis=操作轴)
test = np.array([[1, 2, 3], [2, 3, 4], [5, 4, 3], [8, 7, 2]])
print("test:\n", test)
print("每一列的最大值的索引:", tf.argmax(test, axis=0)) # 返回每一列最大值的索引
print("每一行的最大值的索引", tf.argmax(test, axis=1)) # 返回每一行最大值的索引
四、鸢尾花的分类
神经网络实现鸢尾花的分类流程:
- 准备数据
数据集读入
数据集乱序
生成训练集和测试集
配成(输入特征,标签)对,每次读入batch
- 搭建网络
定义神经网络中所有可训练参数
- 参数优化
嵌套循环迭代,with结构更新参数,显示当前loss
- 测试效果计算当前参数前后
计算当前参数前向传播后的准确率,显示当前acc
- acc/loss可视化
1.从sklearn包datasets读入数据集
from sklearn import datasets
from pandas import DataFrame
import pandas as pd
x_data = datasets.load_iris().data # .data返回iris数据集所有输入特征
y_data = datasets.load_iris().target # .target返回iris数据集所有标签
print("x_data from datasets: \n", x_data)
print("y_data from datasets: \n", y_data)
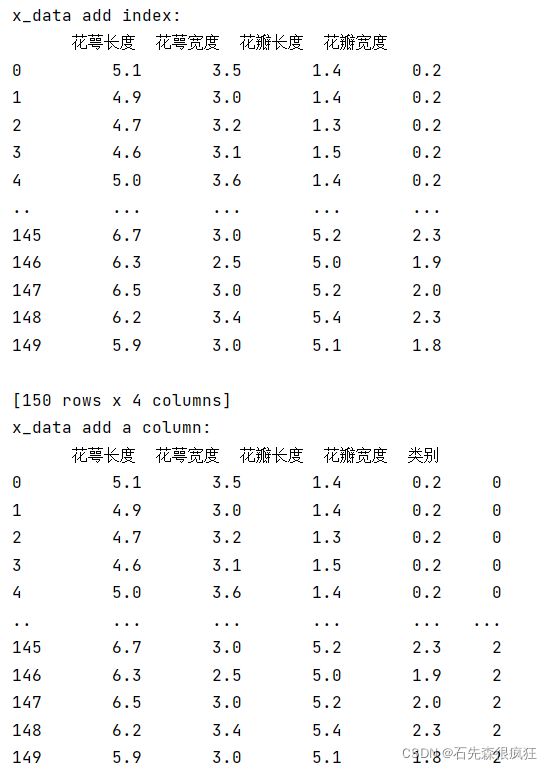
x_data = DataFrame(x_data, columns=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度']) # 为表格增加行索引(左侧)和列标签(上方)
pd.set_option('display.unicode.east_asian_width', True) # 设置列名对齐
print("x_data add index: \n", x_data)
x_data['类别'] = y_data # 新加一列,列标签为‘类别’,数据为y_data
print("x_data add a column: \n", x_data)
#类型维度不确定时,建议用print函数打印出来确认效果
2.神经网络实现鸢尾花的分类
# -*- coding: UTF-8 -*-
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
# 训练部分
for epoch in range(epoch): #数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): #batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all/4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
五、预备知识
1、tf.where(条件语句, 真返回A, 假返回B)
import tensorflow as tf
# tf.where()
# 条件语句真返回A,假返回B
# tf.where(条件语句, 真返回A, 假返回B)
a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
# tf.greater(a, b)判断a>b?
c = tf.where(tf.greater(a, b), a, b) # 若a>b,返回a对应位置的元素,否则返回b对应位置的元素
print("c:", c)
2、np.random.RandomState.rand(维度)
import numpy as np
# np.random.RandomState.rand(维度) 维度为空,返回标量
# 返回一个[0,1]之间的随机数
rdm = np.random.RandomState(seed=1) # seed=常数每次生成随机数相同
a = rdm.rand() # 返回一个随机标量
b = rdm.rand(2, 3) # 返回维度为2行3列随机数矩阵
print("a:", a)
print("b:", b)
3、np.vstack((数组1, 数组2))将两个数据按垂直方向叠加
import numpy as np
# 将两个数据按垂直方向叠加
# np.vstack((数组1, 数组2))
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
c = np.vstack((a, b))
print("c:\n", c)
4、np.mgrid[ ]、 x.ravel()、np.c_[ ]
- np.mgrid[起始值:结束值:步长,起始值:结束值:步长,…]
- x.ravel()将x变为一维数组,“把.前变量拉直”
- np.c_[数值1,数值2]使返回的间隔数值点配对
import numpy as np
import tensorflow as tf
# np.mgrid[起始值:结束值:步长,起始值:结束值:步长,....]
# 生成等间隔数值点
x, y = np.mgrid[1:3:1, 2:4:0.5]
# x.ravel()将x变为一维数组,“把.前变量拉直”
# 将x, y拉直,并合并配对为二维张量,生成二维坐标点
# np.c_[数值1,数值2]使返回的间隔数值点配对
grid = np.c_[x.ravel(), y.ravel()]
print("x:\n", x)
print("y:\n", y)
print("x.ravel():\n", x.ravel())
print("y.ravel():\n", y.ravel())
print('grid:\n', grid)
六、复杂度学习率
1、学习率公式:
2、 如何寻找最优学习率?
import tensorflow as tf
w = tf.Variable(tf.constant(5, dtype=tf.float32))
epoch = 40
LR_BASE = 0.2 # 最初学习率
LR_DECAY = 0.99 # 学习率衰减率
LR_STEP = 1 # 喂入多少轮BATCH_SIZE后,更新一次学习率
for epoch in range(epoch): # for epoch 定义顶层循环,表示对数据集循环epoch次,此例数据集数据仅有1个w,初始化时候constant赋值为5,循环100次迭代。
lr = LR_BASE * LR_DECAY ** (epoch / LR_STEP)
with tf.GradientTape() as tape: # with结构到grads框起了梯度的计算过程。
loss = tf.square(w + 1)
grads = tape.gradient(loss, w) # .gradient函数告知谁对谁求导
w.assign_sub(lr * grads) # .assign_sub 对变量做自减 即:w -= lr*grads 即 w = w - lr*grads
print("After %s epoch,w is %f,loss is %f,lr is %f" % (epoch, w.numpy(), loss, lr))
七、激活函数
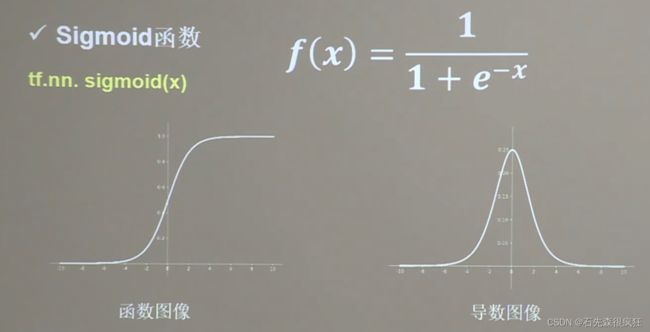
1、Sigmoid函数
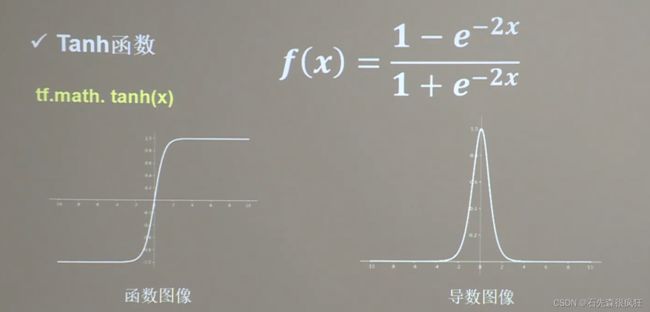
2、Tanh函数
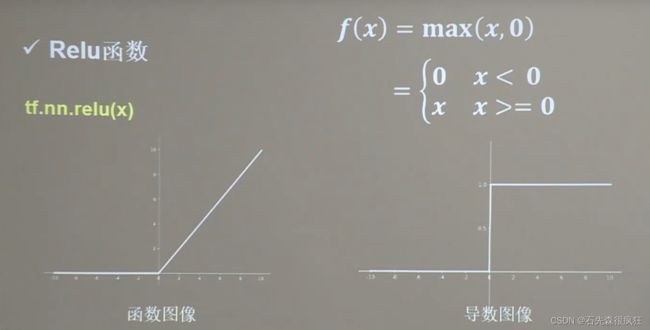
3、Relu函数
- 优点:
- 缺点:
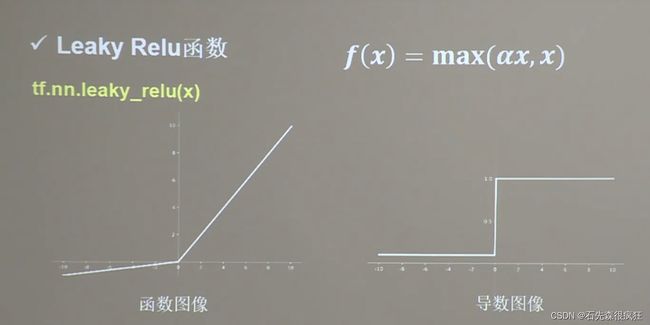
4、Leaky Relu函数
5、softmax函数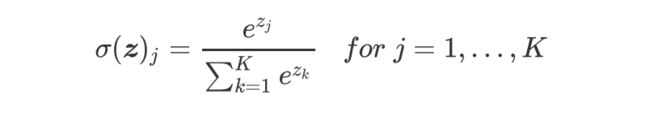
- 特点:对神经网络全连接层输出进行变换,使其服从概率分布,即每个值都位于[0,1]区间且和为1。
6、选择函数建议
八、损失函数
1、均方误差损失函数
实例:
- 预测酸奶日销量y,x1、x2是影响日销量的因素。
- 建模前,应预先采集的数据有:每日x1、x2和销量y_(即已知答案,最佳情况:产量=销量)
- 拟造数据集X,Y_: y_ = x1 + x2 噪声:-0.05 ~ +0.05 拟合可以预测销量的函数
import tensorflow as tf
import numpy as np
# 随机种子,保证随机生成的一样
SEED = 23455
rdm = np.random.RandomState(seed=SEED) # 生成[0,1)之间的随机数
# 生成32行2列的输入特征x包含32组x1,x2(0-1之间随机数)
x = rdm.rand(32, 2)
# (rdm.rand() / 10.0 - 0.05)作为随机噪声加入(-0.05~+0.05)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
# 强制转换数据类型
x = tf.cast(x, dtype=tf.float32)
# 随机初始化参数w1,两行一列
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 15000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
# 求前向传播y
y = tf.matmul(x, w1)
# 求均方误差损失函数
loss_mse = tf.reduce_mean(tf.square(y_ - y))
# 随时函数对参数w1求偏导
grads = tape.gradient(loss_mse, w1)
# 更新参数w1
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
都趋近于1,拟合出的销量Y=1.00x1+1.00x2 与制造数据集Y=1.0x1+1.0x2一致
2、自定义损失函数
如:预测酸奶销量,酸奶成本(COST)1元,酸奶利润(PROFIT)99元。 预测少了损失利润99元,大于预测多了损失成本1元。
预测少了损失大,希望生成的预测函数往多了预测。
import tensorflow as tf
import numpy as np
SEED = 23455
COST = 1
PROFIT = 99
rdm = np.random.RandomState(SEED)
x = rdm.rand(32, 2)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x] # 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 10000
lr = 0.002
for epoch in range(epoch):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
# tf.where(tf.greater(y, y_) 判断y>y_?
# 若y
# 若y>=y_;预测的 y 多了,损失成本(COST)
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * COST, (y_ - y) * PROFIT))
grads = tape.gradient(loss, w1)
w1.assign_sub(lr * grads)
if epoch % 500 == 0:
print("After %d training steps,w1 is " % (epoch))
print(w1.numpy(), "\n")
print("Final w1 is: ", w1.numpy())
# 自定义损失函数
# 酸奶成本1元, 酸奶利润99元
# 成本很低,利润很高,人们希望多预测些,生成模型系数大于1,往多了预测
3、交叉熵损失函数
import tensorflow as tf
loss_ce1 = tf.losses.categorical_crossentropy([1, 0], [0.6, 0.4])
loss_ce2 = tf.losses.categorical_crossentropy([1, 0], [0.8, 0.2])
print("loss_ce1:", loss_ce1)
print("loss_ce2:", loss_ce2)
# 交叉熵损失函数
# softmax与交叉熵损失函数的结合
import tensorflow as tf
import numpy as np
y_ = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y_pro = tf.nn.softmax(y)
loss_ce1 = tf.losses.categorical_crossentropy(y_,y_pro)
loss_ce2 = tf.nn.softmax_cross_entropy_with_logits(y_, y)
print('分步计算的结果:\n', loss_ce1)
print('结合计算的结果:\n', loss_ce2)
# 输出的结果相同
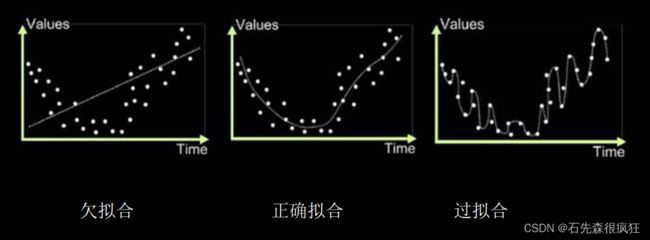
九、欠拟合与过拟合
- 增加输入特征项
- 增加网络参数
- 减少正则化参数
过拟合的解决方法:
- 数据清洗
- 增大训练集
- 采用正则化
- 增大正则化参数
正则化缓解过拟合
正则化在损失函数中引入模型复杂度指标,利用给W加权值,弱化了训练 数据的噪声(一般不正则化b)
正则化的选择
- L1正则化大概率会使很多参数变为零,因此该方法可通过稀疏参数 ,即减少参数的数量,降低复杂度。
- L2正则化会使参数很接近零但不为零,因此该方法可通过减小参数 值的大小降低复杂度。
# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])
x_train = np.vstack(x_data).reshape(-1, 2)
y_train = np.vstack(y_data).reshape(-1, 1)
Y_c = [['red' if y else 'blue'] for y in y_train]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)
# from_tensor_slices函数切分传入的张量的第一个维度,生成相应的数据集,使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
# 定义两层网络
# 生成神经网络的参数,输入层为2个神经元,隐藏层为11个神经元,1层隐藏层,输出层为1个神经元
# 用tf.Variable()保证参数可训练
# 2是第一层网络,11是网络的输出个数
#
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
# 11是因为网络的输入个数=网络的输出个数
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
lr = 0.005 # 学习率
epoch = 800 # 循环轮数
# 训练部分
for epoch in range(epoch):
for step, (x_train, y_train) in enumerate(train_db):
with tf.GradientTape() as tape: # 记录梯度信息
h1 = tf.matmul(x_train, w1) + b1 # 记录神经网络乘加运算
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss = tf.reduce_mean(tf.square(y_train - y))
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 实现梯度更新
# w1 = w1 - lr * w1_grad tape.gradient是自动求导结果与[w1, b1, w2, b2] 索引为0,1,2,3
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
# 每20个epoch,打印loss信息
if epoch % 20 == 0:
print('epoch:', epoch, 'loss:', float(loss))
# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01,yy在-3到3之间以步长0.01,生成间隔数值点
# 生成网格坐标点,密度是0.1
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx , yy拉直,并合并配对为二维张量,生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络,进行预测,probs为输出
probs = []
for x_test in grid:
# 使用训练好的参数进行预测
h1 = tf.matmul([x_test], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2 # y为预测结果
probs.append(y)
# 取第0列给x1,取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
# 画出x1,x2散点
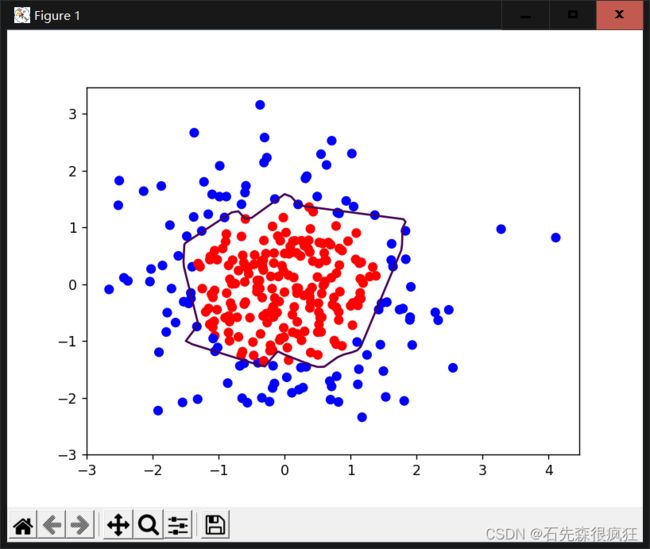
plt.scatter(x1, x2, color=np.squeeze(Y_c)) # squeeze去掉纬度是1的纬度,相当于去掉[['red'],[''blue]],内层括号变为['red','blue']
# 把坐标xx yy和对应的值probs放入contour函数,给probs值为0.5的所有点上色 plt.show()后 显示的是红蓝点的分界线
# 画出预测值为0.5的曲线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()
# 读入红蓝点,画出分割线,不包含正则化
# 不清楚的数据,建议print出来查看
加入来L2正则化代码实现:
# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])
x_train = x_data
y_train = y_data.reshape(-1, 1)
Y_c = [['red' if y else 'blue'] for y in y_train]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)
# from_tensor_slices函数切分传入的张量的第一个维度,生成相应的数据集,使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
# 生成神经网络的参数,输入层为4个神经元,隐藏层为32个神经元,2层隐藏层,输出层为3个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
lr = 0.005 # 学习率为
epoch = 800 # 循环轮数
# 训练部分
for epoch in range(epoch):
for step, (x_train, y_train) in enumerate(train_db):
with tf.GradientTape() as tape: # 记录梯度信息
h1 = tf.matmul(x_train, w1) + b1 # 记录神经网络乘加运算
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_mse = tf.reduce_mean(tf.square(y_train - y))
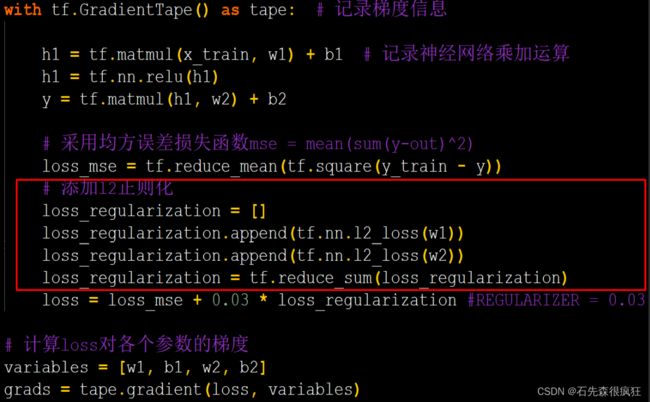
# 添加l2正则化
loss_regularization = []
# tf.nn.l2_loss(w)=sum(w ** 2) / 2
loss_regularization.append(tf.nn.l2_loss(w1))
loss_regularization.append(tf.nn.l2_loss(w2))
# 求和
# 例:x=tf.constant(([1,1,1],[1,1,1]))
# tf.reduce_sum(x)
# >>>6
loss_regularization = tf.reduce_sum(loss_regularization)
loss = loss_mse + 0.03 * loss_regularization # REGULARIZER = 0.03
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 实现梯度更新
# w1 = w1 - lr * w1_grad
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
# 每200个epoch,打印loss信息
if epoch % 20 == 0:
print('epoch:', epoch, 'loss:', float(loss))
# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01,yy在-3到3之间以步长0.01,生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx, yy拉直,并合并配对为二维张量,生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络,进行预测,probs为输出
probs = []
for x_predict in grid:
# 使用训练好的参数进行预测
h1 = tf.matmul([x_predict], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2 # y为预测结果
probs.append(y)
# 取第0列给x1,取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c))
# 把坐标xx yy和对应的值probs放入contour函数,给probs值为0.5的所有点上色 plt.show()后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()
# 读入红蓝点,画出分割线,包含正则化
# 不清楚的数据,建议print出来查看
预测结果:
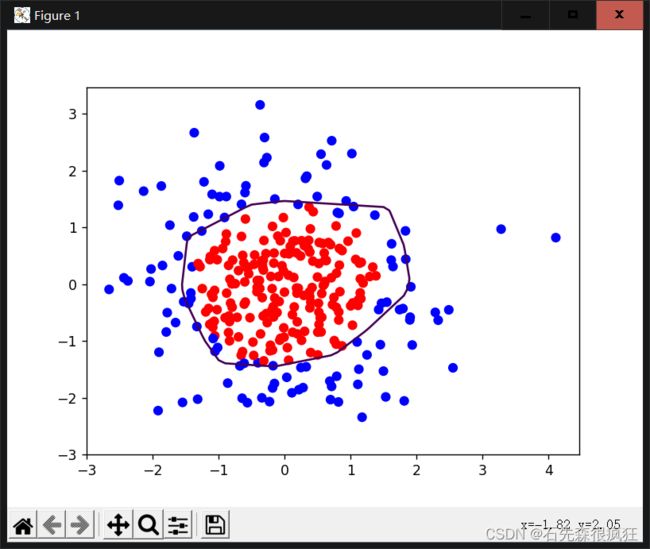
从结果可以看出加入L2的正则化曲线更平缓,有效缓解了过拟合!
十、优化器
优化算法可以分成一阶优化和二阶优化算法,其中一阶优化就是指的梯度算法及其变种,而二阶优 化一般是用二阶导数(Hessian矩阵)来计算,
如牛顿法,由于需要计算Hessian阵和其逆矩阵,计算 量较大,因此没有流行开来。这里主要总结一阶优化的各种梯度下降方法。
待优化参数优化器框架,损失函数oss,学习率er,每次迭代一个bacth,表示当前batch迭代的总次数:

1.SGD随机梯度下降
单层网络代码实现:
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1## # 时间模块 时间戳
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
# 训练部分
now_time = time.time() ##2## #记录训练起始时间
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
# 实现梯度更新 w1 = w1 - lr * w1_grad b = b - lr * b_grad
w1.assign_sub(lr * grads[0]) # 参数w1自更新
b1.assign_sub(lr * grads[1]) # 参数b自更新
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4## # 训练结束时间
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
# 本文件较 class1\p45_iris.py 仅添加四处时间记录 用 ##n## 标识
# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx 对比各优化器收敛情况
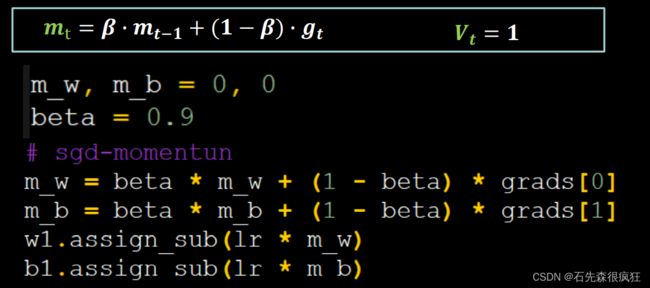
2.SGDM
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
m_w, m_b = 0, 0
beta = 0.9
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# sgd-momentun
m_w = beta * m_w + (1 - beta) * grads[0]
m_b = beta * m_b + (1 - beta) * grads[1]
w1.assign_sub(lr * m_w)
b1.assign_sub(lr * m_b)
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4##
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx 对比各优化器收敛情况
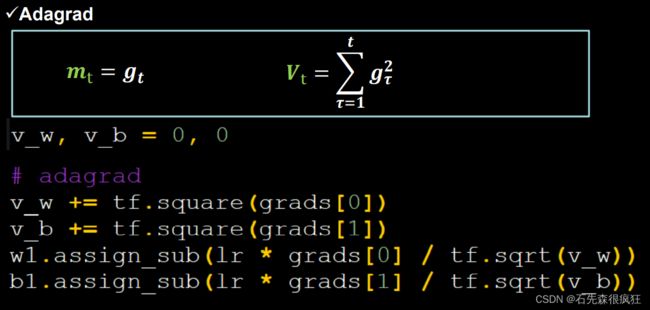
3.Adagrad,在SGD基础上增加二阶动量
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
v_w, v_b = 0, 0
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# adagrad
v_w += tf.square(grads[0])
v_b += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4##
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx 对比各优化器收敛情况
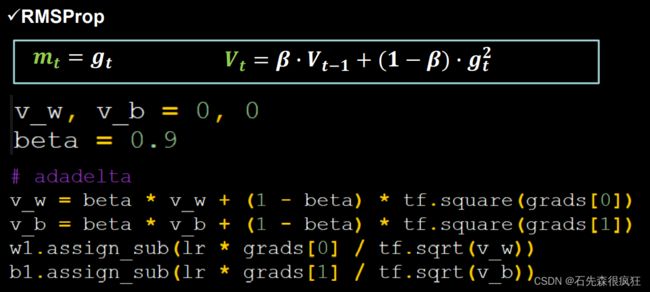
4.RMSProp,SGD基础上增加二阶动量
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
v_w, v_b = 0, 0
beta = 0.9
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# rmsprop
v_w = beta * v_w + (1 - beta) * tf.square(grads[0])
v_b = beta * v_b + (1 - beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(v_w))
b1.assign_sub(lr * grads[1] / tf.sqrt(v_b))
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4##
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx 对比各优化器收敛情况
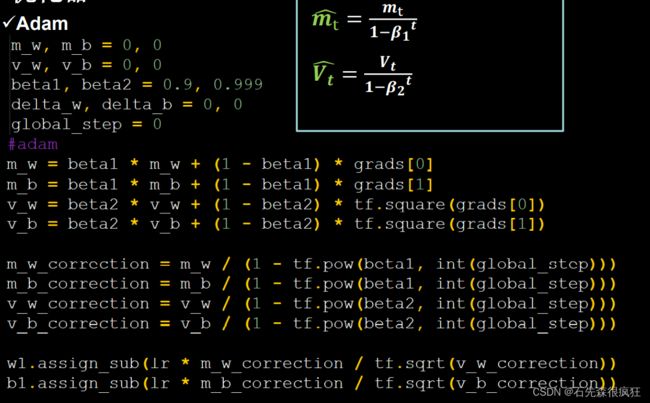
5.Adam, 同时结合SGDM一阶动量和RMSProp二阶动量
# 利用鸢尾花数据集,实现前向传播、反向传播,可视化loss曲线
# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np
import time ##1##
# 导入数据,分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target
# 随机打乱数据(因为原始数据是顺序的,顺序不打乱会影响准确率)
# seed: 随机数种子,是一个整数,当设置之后,每次生成的随机数都一样(为方便教学,以保每位同学结果一致)
np.random.seed(116) # 使用相同的seed,保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)
# 将打乱后的数据集分割为训练集和测试集,训练集为前120行,测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)
# from_tensor_slices函数使输入特征和标签值一一对应。(把数据集分批次,每个批次batch组数据)
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)
# 生成神经网络的参数,4个输入特征故,输入层为4个输入节点;因为3分类,故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同(方便教学,使大家结果都一致,在现实使用时不写seed)
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))
lr = 0.1 # 学习率为0.1
train_loss_results = [] # 将每轮的loss记录在此列表中,为后续画loss曲线提供数据
test_acc = [] # 将每轮的acc记录在此列表中,为后续画acc曲线提供数据
epoch = 500 # 循环500轮
loss_all = 0 # 每轮分4个step,loss_all记录四个step生成的4个loss的和
##########################################################################
m_w, m_b = 0, 0
v_w, v_b = 0, 0
beta1, beta2 = 0.9, 0.999
delta_w, delta_b = 0, 0
global_step = 0
##########################################################################
# 训练部分
now_time = time.time() ##2##
for epoch in range(epoch): # 数据集级别的循环,每个epoch循环一次数据集
for step, (x_train, y_train) in enumerate(train_db): # batch级别的循环 ,每个step循环一个batch
##########################################################################
global_step += 1
##########################################################################
with tf.GradientTape() as tape: # with结构记录梯度信息
y = tf.matmul(x_train, w1) + b1 # 神经网络乘加运算
y = tf.nn.softmax(y) # 使输出y符合概率分布(此操作后与独热码同量级,可相减求loss)
y_ = tf.one_hot(y_train, depth=3) # 将标签值转换为独热码格式,方便计算loss和accuracy
loss = tf.reduce_mean(tf.square(y_ - y)) # 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_all += loss.numpy() # 将每个step计算出的loss累加,为后续求loss平均值提供数据,这样计算的loss更准确
# 计算loss对各个参数的梯度
grads = tape.gradient(loss, [w1, b1])
##########################################################################
# adam
m_w = beta1 * m_w + (1 - beta1) * grads[0]
m_b = beta1 * m_b + (1 - beta1) * grads[1]
v_w = beta2 * v_w + (1 - beta2) * tf.square(grads[0])
v_b = beta2 * v_b + (1 - beta2) * tf.square(grads[1])
m_w_correction = m_w / (1 - tf.pow(beta1, int(global_step)))
m_b_correction = m_b / (1 - tf.pow(beta1, int(global_step)))
v_w_correction = v_w / (1 - tf.pow(beta2, int(global_step)))
v_b_correction = v_b / (1 - tf.pow(beta2, int(global_step)))
w1.assign_sub(lr * m_w_correction / tf.sqrt(v_w_correction))
b1.assign_sub(lr * m_b_correction / tf.sqrt(v_b_correction))
##########################################################################
# 每个epoch,打印loss信息
print("Epoch {}, loss: {}".format(epoch, loss_all / 4))
train_loss_results.append(loss_all / 4) # 将4个step的loss求平均记录在此变量中
loss_all = 0 # loss_all归零,为记录下一个epoch的loss做准备
# 测试部分
# total_correct为预测对的样本个数, total_number为测试的总样本数,将这两个变量都初始化为0
total_correct, total_number = 0, 0
for x_test, y_test in test_db:
# 使用更新后的参数进行预测
y = tf.matmul(x_test, w1) + b1
y = tf.nn.softmax(y)
pred = tf.argmax(y, axis=1) # 返回y中最大值的索引,即预测的分类
# 将pred转换为y_test的数据类型
pred = tf.cast(pred, dtype=y_test.dtype)
# 若分类正确,则correct=1,否则为0,将bool型的结果转换为int型
correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
# 将每个batch的correct数加起来
correct = tf.reduce_sum(correct)
# 将所有batch中的correct数加起来
total_correct += int(correct)
# total_number为测试的总样本数,也就是x_test的行数,shape[0]返回变量的行数
total_number += x_test.shape[0]
# 总的准确率等于total_correct/total_number
acc = total_correct / total_number
test_acc.append(acc)
print("Test_acc:", acc)
print("--------------------------")
total_time = time.time() - now_time ##3##
print("total_time", total_time) ##4##
# 绘制 loss 曲线
plt.title('Loss Function Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Loss') # y轴变量名称
plt.plot(train_loss_results, label="$Loss$") # 逐点画出trian_loss_results值并连线,连线图标是Loss
plt.legend() # 画出曲线图标
plt.show() # 画出图像
# 绘制 Accuracy 曲线
plt.title('Acc Curve') # 图片标题
plt.xlabel('Epoch') # x轴变量名称
plt.ylabel('Acc') # y轴变量名称
plt.plot(test_acc, label="$Accuracy$") # 逐点画出test_acc值并连线,连线图标是Accuracy
plt.legend()
plt.show()
# 请将loss曲线、ACC曲线、total_time记录到 class2\优化器对比.docx 对比各优化器收敛情况
十一、搭建网络八股
总结
本文章不断更新中,欢迎与大家一起学习