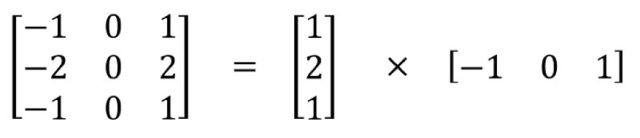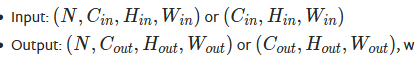不同卷积方法一览（+部分代码）

关键词

卷积方法：2D / 3D / 1x1 /转置/扩张（Atrous）/空间可分/深度可分/平展/分组/混洗分组/逐点分组卷积

卷积网络：全卷积FCN（Fully Convolutional Network），可变形卷积（Deformable Convolutional Network）

---

2D卷积

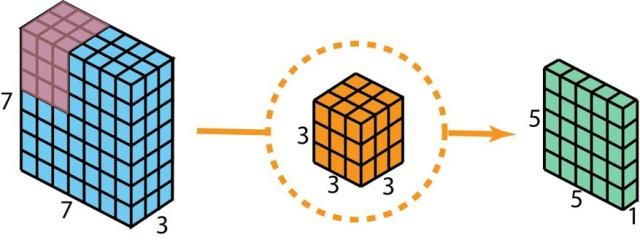
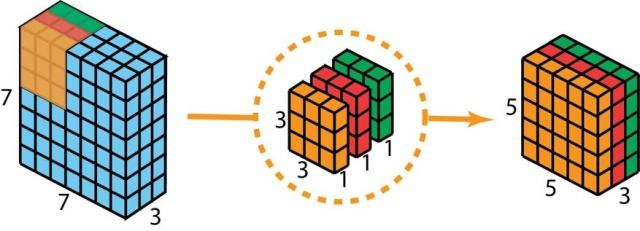
假设输入层的大小是 7×7×3（高×宽×通道），而过滤器的大小是 3×3×3。经过与一个过滤器的 2D 卷积之后，输出层的大小是 5×5×1（仅有一个通道）。使用多个过滤器就会有多个通道。

3D卷积

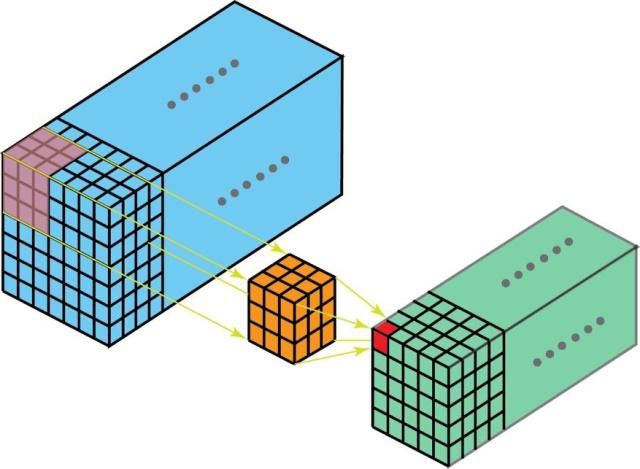
3D 卷积是 2D 卷积的泛化。下面就是 3D 卷积，其过滤器深度小于输入层深度（核大小<通道大小）。因此，3D 过滤器可以在所有三个方向（图像的高度、宽度、通道）上移动。在每个位置，逐元素的乘法和加法都会提供一个数值。因为过滤器是滑过一个 3D 空间，所以输出数值也按 3D 空间排布。也就是说输出是一个 3D 数据。

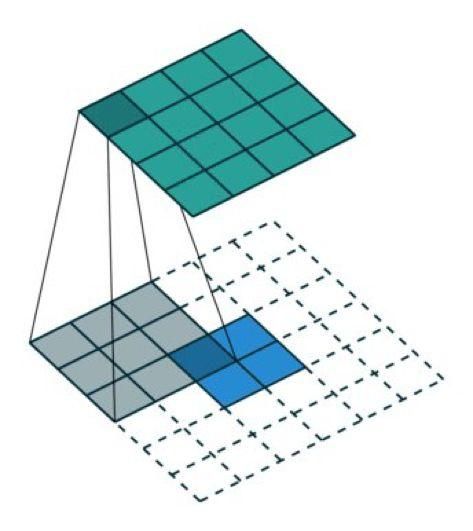
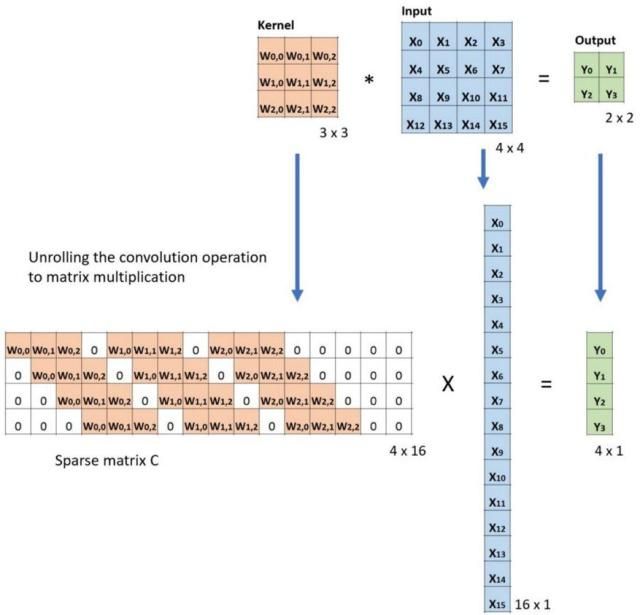
转置卷积（去卷积）TransposedConv

使用卷积来上采样

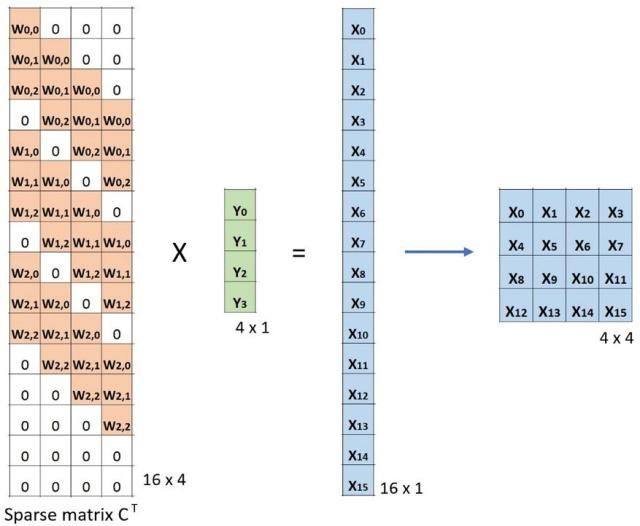
转置卷积的转置来源：矩阵与其转置矩阵的乘法得到一个单位矩阵

#tensorflow v2.9
#输入矩阵之间的空自动填充
tf.keras.layers.Conv2DTranspose(
    filters,       #卷积核个数
    kernel_size,    #卷积核大小
    strides=(1, 1),  #卷积核步长大小 （与空洞大小不能都不为1）
    padding='valid',
    output_padding=None,    #输出的填充
    data_format=None,
    dilation_rate=(1, 1),    #卷积核空洞大小
    activation=None,
    use_bias=True,
    kernel_initializer='glorot_uniform',
    bias_initializer='zeros',
    kernel_regularizer=None,
    bias_regularizer=None,
    activity_regularizer=None,
    kernel_constraint=None,
    bias_constraint=None,
    **kwargs
)

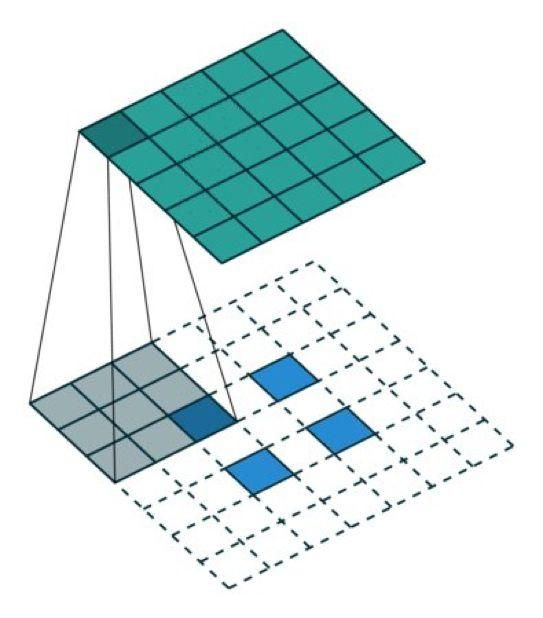
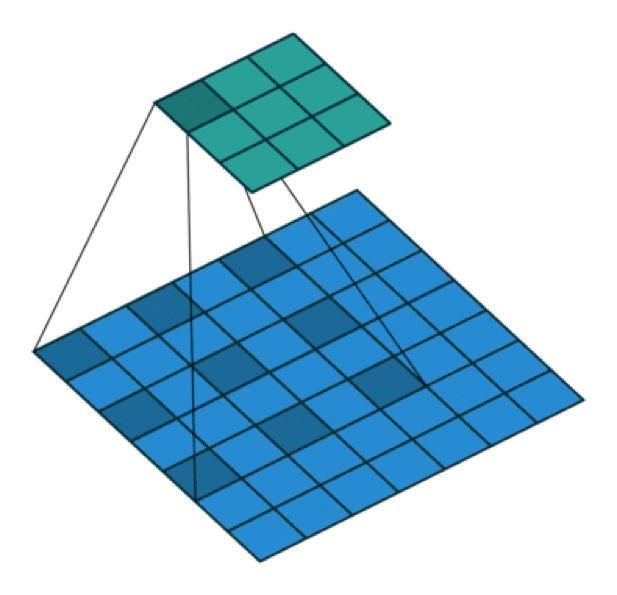
扩张卷积（Atrous 卷积）(Dilated Convolution)

直观而言，扩张卷积就是通过在核元素之间插入空格来使核「膨胀」。新增的参数 l（扩张率）表示我们希望将核加宽的程度。具体实现可能各不相同，但通常是在核元素之间插入 l-1 个空格。

可分卷积Separable Conv

可分卷积有空间可分卷积和深度可分卷积。某些神经网络架构比如 MobileNets使用了可分卷积。

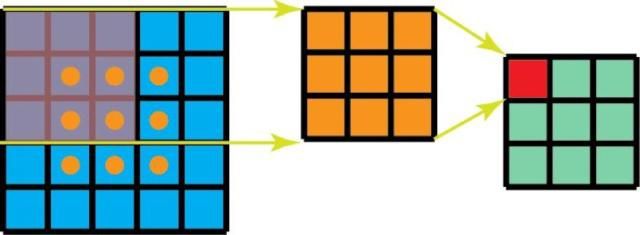
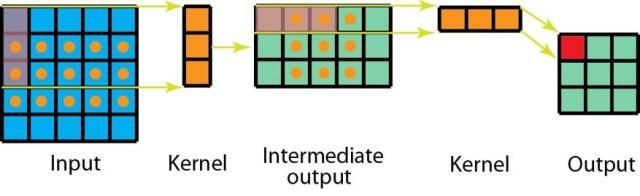
空间可分卷积

空间可分卷积操作的是图像的 2D 空间维度，即高和宽。从概念上看，空间可分卷积是将一个卷积分解为两个单独的运算。比如将3x3的Sobel 核被分成了一个 3×1 核和一个 1×3 核

 此外，使用空间可分卷积时所需的矩阵乘法也更少

尽管空间可分卷积能节省成本，但深度学习却很少使用它。一大主要原因是并非所有的核都能分成两个更小的核。如果我们用空间可分卷积替代所有的传统卷积，那么我们就限制了自己在训练过程中搜索所有可能的核。这样得到的训练结果可能是次优的。

深度可分卷积 Depthwise Convolution

相比2D卷积，深度卷积分开使用 3 个核。每个过滤器的大小为 3×3×1。每个核与输入层的一个通道卷积（仅一个通道，而非所有通道！）。每个这样的卷积都能提供大小为 5×5×1 的映射图。然后我们将这些映射图堆叠在一起，创建一个 5×5×3 的图像。

深度可分卷积效率优势很大，但会降低卷积中参数的数量。因此，对于较小的模型而言，如果用深度可分卷积替代 2D 卷积，模型的能力可能会显著下降。

分组卷积Grouped conv

分组个数和通道数一致的话就是深度可分卷积。起初被AlexNet用于并行化计算

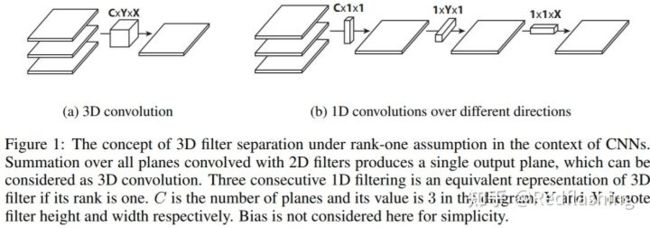
平展卷积

直觉上看，平展卷积的理念是滤波器分离。我们不应用一个标准的滤波器将输入映射到输出，而是将此标准的滤波器分解为3个1D滤波器。这种想法与上述空间可分卷积类似，其中的一个空间滤波器近似于两个 rank-1 过滤器（秩1矩阵），而秩1矩阵可表示为一列基乘以一行基的形式A=UV^T，最后分解得到3个1D滤波器。

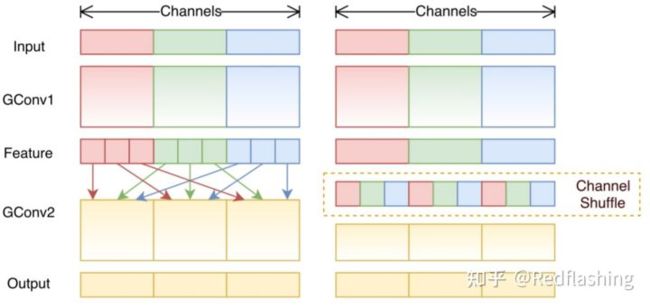
混洗分组卷积（Shuffled Grouped Convolution）

ShuffleNet中提出的一种计算效率非常高的卷积结构，随机分组卷积涉及分组卷积和通道混洗。通道混洗操作（Channel Shuffle Operation）的想法是，我们希望混合来自不同筛选器组的信息。由于经过混洗后信息已经混合，因此，通过允许通道之间的信息交换，增强了模型的表现力。

逐点分组卷积（Pointwise Grouped Convolution）

通常对于分组卷积（如 MobileNet或 ResNeXt，组操作在3 x 3空间卷积上执行，但在1 x 1卷积上不执行。ShuffleNet论文认为，1 x 1卷积在计算上也是昂贵的。并建议在1 x 1卷积上也应用分组卷积。顾名思义，逐点分组卷积执行1 x 1卷积的组操作。该操作与分组卷积相同，只有一个修改在1 x 1筛选器上执行，而不是n x n滤波器 （n>1）。

 

全卷积FCN（Fully Convolutional Network）

CNN的全连接是实现图像的分类，而FCN则是用全卷积实现对图像的分割（每一个像素的分类）

比如说1000分类任务，CNN输出为1000x1的话，FCN输出的结果为1000xHxW

FCN使用反卷积的上采样和跳级结构skips：

• 跳级结构将最后一层的预测（富有全局信息）和更浅层（富有局部信息）的预测结合起来，在遵守全局预测的同时进行局部预测。
• 跳级结构中是求和而不是取最大值：求和更容易求导，从而反向传播
• FCN的不足：得到的结果还不够精细，对细节不够敏感；未考虑像素与像素之间的关系，缺乏空间一致性等

FCN-8s 网络—升采样分为三次完成。 进一步融合了第3个pooling层的预测结果：

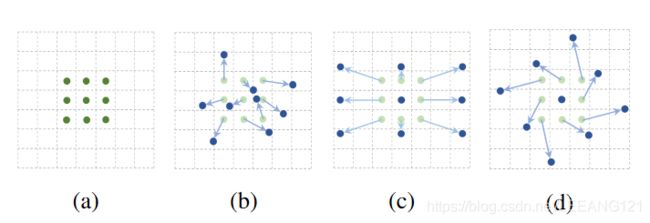
可变形卷积DCN（2017）

可变形卷积在每一个元素上额外增加了一个参数方向参数, 使得卷积核可以根据实际情况调整本身的形状，更好的提取输入的特征

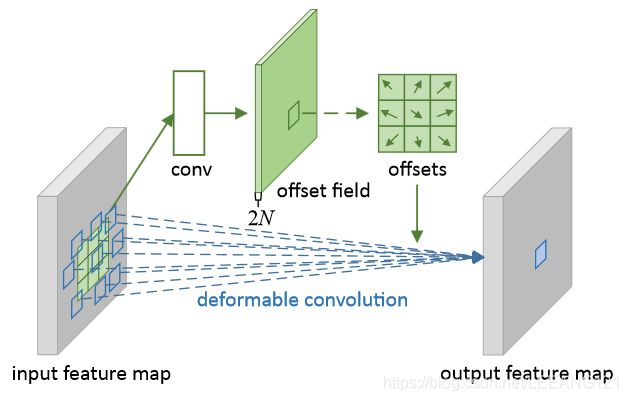
可变形卷积的学习过程： 首先偏差(offset)是通过一个卷积层获得，该卷积层的卷积核与普通卷积核一样。输出的偏差尺寸和输入的特征图尺寸一致。生成通道维度是2N，分别对应原始输出特征和偏移特征。这两个卷积核通过双线性插值后向传播算法同时学习。

具体实现方法：

1. 首先，和CNN一样，根据输入的图像，利用传统的卷积核提取特征图。
2. 把得到的特征图作为输入，对特征图再施加一个卷积层，得到可变形卷积的变形的偏移量
3. 偏移层是2N，是因为我们在平面上做平移，需要改变 x和 y 值两个方向。
4. 在训练的时候，用于生成输出特征的卷积核和用于生成偏移量的卷积核是同步学习的。其中偏移量的学习是利用插值算法，通过反向传播进行学习。

计算类似Spatial Transformer Networks（STN）

---

Pytorch代码

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

输入输出形状：

dilation 参数控制kernel的间隔

groups 参数控制分组卷积（深度可分卷积）。in_channels 和 out_channels 需要能被 groups整除。

• At groups=1, all inputs are convolved to all outputs.

• At groups=2, the operation becomes equivalent to having two conv layers side by side, each seeing half the input channels and producing half the output channels, and both subsequently concatenated.

• At groups= in_channels, each input channel is convolved with its own set of filters (of size out_channels / in_channels​).

---

拓展：更多的卷积

• GhostNet：堆叠卷积层
• SCConv：自校正卷积，长距离空间和通道依赖性的校准操作
• DO-Conv：传统卷积和深度卷积结合
• 内卷(Involution)：内卷核由原图像信息通过变换函数得到

---

References

卷积有多少种？一文读懂深度学习中的各种卷积

详述Deep Learning中的各种卷积（四） - 知乎