【AI理论学习】n-gram语言模型和神经网络语言模型
n-gram语言模型和神经网络语言模型
- 什么是语言模型
- 语言模型的计算
- 什么是n-gram模型
- n-gram平滑技术
- 什么是神经网络语言模型(NNLM)?
-
- 基于前馈神经网络的模型
- 基于循环神经网络的模型
- 语言模型评价指标
- 总结
- 参考资料
什么是语言模型
语言模型是自然语言处理中的重要技术,假设一段长度为 T T T的文本中的词依次为 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT,语言模型将计算该序列的概率: P ( w 1 , w 2 , . . . , w T ) P(w_1,w_2,...,w_T) P(w1,w2,...,wT)
语言模型有助于提升自然语言处理任务的效果,例如在语音识别任务中,给定一段“厨房里食油用完了”的语音,有可能会输出“厨房里食油用完了”和“厨房里石油用完了”这两个读音完全一样的文本序列。合适的语言模型能够判断出前者的概率大于后者的概率,于是可以得到正确的“厨房里食油用完了”这个文本序列。
语言模型的计算
把文本看作一段离散的时间序列 w 1 , w 2 , … , w T w_1, w_2, \ldots, w_T w1,w2,…,wT,假设每个词是按时间先后顺序依次生成的,那么在离散的时间序列中, w t ( 1 ≤ t ≤ T ) w_t(1 \leq t \leq T) wt(1≤t≤T)可看作在时间步(time step) t t t的输出或标签。于是,对于一个句子而言,有:
P ( w 1 , w 2 , … , w T ) = ∏ t = 1 T P ( w t ∣ w 1 , … , w t − 1 ) P(w_1, w_2, \ldots, w_T) = \prod_{t=1}^T P(w_t \mid w_1, \ldots, w_{t-1}) P(w1,w2,…,wT)=t=1∏TP(wt∣w1,…,wt−1).
例如,一段含有4个词的文本序列的概率:
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 1 , w 2 , w 3 ) P(w_1, w_2, w_3, w_4) = P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3) P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3).
什么是n-gram模型
N-Gram是一种基于统计语言模型的算法。它的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作,形成了长度是N的字节片段序列。
每一个字节片段称为gram,对所有gram的出现频度进行统计,并且按照事先设定好的阈值进行过滤,形成关键gram列表,也就是这个文本的向量特征空间,列表中的每一种gram就是一个特征向量维度。
n-gram 模型基于马尔可夫假设,第n个词的出现只与前面 n-1 个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积:
P ( w 1 , w 2 , … , w T ) ≈ ∏ t = 1 T P ( w t ∣ w t − ( n − 1 ) , … , w t − 1 ) P(w_1, w_2, \ldots, w_T) \approx \prod_{t=1}^T P(w_t \mid w_{t-(n-1)}, \ldots, w_{t-1}) P(w1,w2,…,wT)≈t=1∏TP(wt∣wt−(n−1),…,wt−1) .
该模型基于这样一种假设,第N个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。
例如,长度为4的序列 w 1 , w 2 , w 3 , w 4 w_1, w_2, w_3, w_4 w1,w2,w3,w4 在Bi-Gram和Tri-Gram中的概率分别为:
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 2 ) P ( w 4 ∣ w 3 ) P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3) P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w2)P(w4∣w3),
P ( w 1 , w 2 , w 3 , w 4 ) = P ( w 1 ) P ( w 2 ∣ w 1 ) P ( w 3 ∣ w 1 , w 2 ) P ( w 4 ∣ w 2 , w 3 ) P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w2,w3) P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w2,w3)
当 n n n较小时, n n n元语法往往并不准确。然而,当 n n n较大时, n n n元语法需要计算并存储大量的词频和多词相邻频率。
对于Bi-Gram而言,有:
p ( w t ∣ w t − 1 ) = c ( w t − 1 , w t ) ∑ w t c ( w t − 1 , w t ) p(w_t|w_{t-1}) = \frac{c(w_{t-1},w_t)}{\sum_{w_t}c(w_{t-1},w_t)} p(wt∣wt−1)=∑wtc(wt−1,wt)c(wt−1,wt)
当 t = 1 t=1 t=1时,为了使上式有意义,在句子的开头加上 < B O S >
下面举个例子:使用自己构建的小型语料库
商品 和 服务
商品 和服 物美价廉
服务 和 货币
我 打 篮球
我 打 游泳

随着n的取值越大,n-gram模型在理论上越精确,但是也越复杂,需要的计算量和训练语料数据量也就越大,并且精度提升的不够明显,所以在实际的任务中很少使用n ≥ 4的语言模型。
n-gram平滑技术
无论是原始的语言模型还是n-gram语言模型,都是使用极大似然估计法来估计概率值,通过统计频次来近似概率值,统计频次极有可能统计不到较长句子的频次。
- 如果分子为0,估计的概率值为0,由于连乘的方式会导致最终计算出句子的概率值为0;
- 如果分母为0,分母为0,计算的公式将没有任何意义;
这被称为数据稀疏,对于n-gram语言模型来说,n越大,数据稀疏的问题越严重。即使是使用n相对比较小的二元语言模型,许多二元靠语料库也是统计不到的。
这也就是说,在自然语言处理处理中,难免会遇到未登录词(OOV),即测试集中出现了训练集中未出现过的词,或者未出现过的子序列,导致语言模型计算出的概率为0。比如对于下面这个小型的语料库:
商品 和 服务
商品 和服 物美价廉
服务 和 货币
"商品 货币"的频次就为0,当n-gram语言模型中的n越小,可统计的n元也就越丰富,一个很自然的解决方案就是利用低阶n元语法平滑到高阶n元语法。所谓的平滑就是字面上的意思:使n元语法频次的折线平滑为曲线。我们不希望二元语法"商品 货币"的频次突然跌倒0,因此使用一元语法"商品"和(“或”,不同的平滑方法可能需要不同的处理)"货币"的频次去平滑它。
使用平滑技术的目的就是在条件概率为0时,防止整个句子的概率为0,人为按一定规则,给0条件概率一定的值。常见的平滑方法有:
- 加法平滑方法
- 古德-图灵(Good-Turing)估计法
- Katz平滑方法
- Jelinek-Mercer平滑方法
- Witten-Bell平滑方法
- 绝对减值法
总结基于统计的 n-gram 语言模型的优缺点:
优点:①采用极大似然估计,参数易训练;②完全包含了前 n-1 个词的全部信息;③可解释性强,直观易理解;
缺点:①缺乏长期依赖,只能建模到前 n-1 个词;②随着 n 的增大,参数空间呈指数增长;③数据稀疏,难免会出现OOV的问题;④单纯的基于统计频次,泛化能力差;
什么是神经网络语言模型(NNLM)?
神经网络语言模型先给每个词赋予一个词向量,利用神经网络去建模当前词出现的概率与其前 n-1 个词之间的约束关系,即通过神经网络去学习词的向量表示。
基于前馈神经网络的模型
基于前馈神经网络的模型如下图所示:

先给每个词在连续空间中赋予一个向量(词向量),再通过神经网络去学习这种分布式表征。利用神经网络去建模当前词出现的概率与其前 n-1 个词之间的约束关系。
很显然这种方式相比 n-gram 具有更好的泛化能力,只要词表征足够好。从而很大程度地降低了数据稀疏带来的问题。但是这个结构的明显缺点是仅包含了有限的前文信息。
具体而言,假设当前词出现的概率只依赖于前 n − 1 n-1 n−1个词。即:
p ( w t ∣ w 1 , . . . , w t − 1 ) = p ( w t ∣ w t − n + 1 , . . . , w t − 1 ) p(w_t|w_1,...,w_{t-1})=p(w_t|w_{t-n+1},...,w_{t-1}) p(wt∣w1,...,wt−1)=p(wt∣wt−n+1,...,wt−1)
假设 V V V表示所有 N N N个词的集合, w t ∈ V w_t\in V wt∈V,存在一个 ∣ V ∣ × m |V|\times m ∣V∣×m的参数矩阵 C C C,矩阵的每一行代表一个词的特征向量, m m m代表每个特征向量有 m m m个维度。 C ( w t ) C(w_t) C(wt)表示第 t t t个词 w t w_t wt的对应的特征向量。
如上图所示,将句子的前n-1个词特征对应的向量 C ( w t − n + 1 ) . . . C ( w t − 1 ) C(w_{t-n+1})...C(w_{t-1}) C(wt−n+1)...C(wt−1)作为神经网络的输入,输出当前词是 w t w_t wt的概率。计算过程如下: y = b + W x + U tanh ( d + H x ) y=b+Wx+U\tanh (d+Hx) y=b+Wx+Utanh(d+Hx)
其中, x = ( C ( w t − 1 ) , C ( w t − 2 ) , ⋅ ⋅ ⋅ , C ( w t − n + 1 ) ) x = (C(w_{t−1}),C(w_{t−2}),··· ,C(w_{t−n+1})) x=(C(wt−1),C(wt−2),⋅⋅⋅,C(wt−n+1))
经过上式得到 y w = ( y w , 1 , y w , e , . . . , y w , N ) T y_w=(y_{w,1},y_{w,e},...,y_{w,N})^T yw=(yw,1,yw,e,...,yw,N)T,其中,将 y w y_w yw进行softmax之后, y w , i y_{w,i} yw,i表示当上下文为context(w)时,下一个词切好是词典中第 i i i个词的概率,即: P ( w ∣ c o n t e x t ( w ) ) = e y w , i w ∑ i = 1 N e y w , i P(w|context(w))=\frac{e^{y_{w,i_w}}}{\sum_{i=1}^Ne^{y_{w,i}}} P(w∣context(w))=∑i=1Neyw,ieyw,iw
其中, i w i_w iw表示词在词典中的索引。
计算集中在隐藏层和输出层之间的矩阵向量运算,以及输出层上的softmax归一化运算。该模型的参数是: θ = ( b , d , W , U , C ) \theta=(b,d,W,U,C) θ=(b,d,W,U,C)
损失函数是:
L = − 1 T ∑ t log p ^ ( w t = i ∣ w t − n + 1 , . . . , w t − 1 ) + R ( θ ) L=-\frac{1}{T}\sum_t \log \hat{p}(w_t=i|w_{t-n+1},...,w_{t-1})+R(\theta) L=−T1t∑logp^(wt=i∣wt−n+1,...,wt−1)+R(θ)
R ( θ ) R(\theta) R(θ)是正则化项,用于控制过拟合。
有了损失函数,我们可以用梯度下降法,在给定学习率 η \eta η的条件下,进行参数更新:更新: θ ← θ − η ∂ L ∂ θ \theta \leftarrow \theta - \eta \frac{\partial L}{\partial \theta} θ←θ−η∂θ∂L直至收敛,得到一组最优参数。
基于循环神经网络的模型
为了解决定长信息的问题,Mikolov 于2010年发表的论文 Recurrent neural network based language model 正式揭开了循环神经网络(RNN)在语言模型中的强大历程。
注意力机制(attention mechanism)应用在 seq2seq 中也是为了克服 encoder 对任意句子只能给出一个固定size的表征,而这个表征在遇到长句时则显得包含信息量不够。
以序列“我想你”为例介绍RNN语言模型的建模过程:
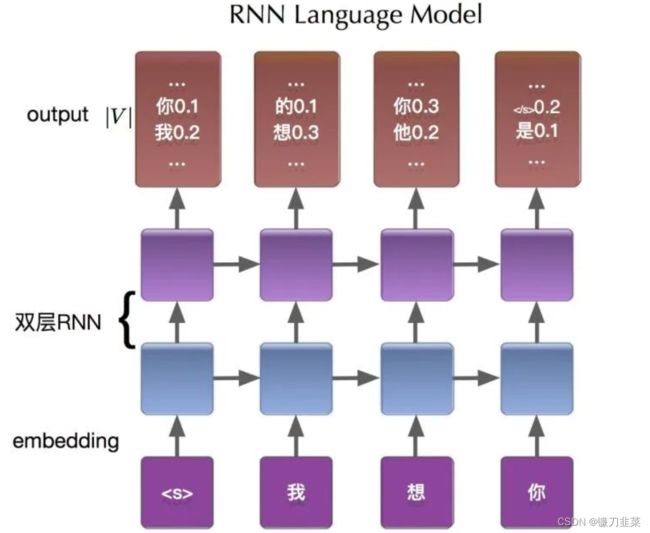
在统计语言模型中,介绍过需要给序列添加起始符和结束符,神经网络语言模型也不例外。网络的输入层是" < s > 我想你 我想你 <s>我想你",输出层可以看作是分别计算条件概率 P ( w ∣ < s > ) P(w|) P(w∣<s>)、 P ( w ∣ < s > 我 ) P(w|我) P(w∣<s>我)、 P ( w ∣ < s > 我想 ) P(w|我想) P(w∣<s>我想)、 P ( w ∣ < s > 我想你 ) P(w|我想你) P(w∣<s>我想你)在整个词表图片中值。而我们的目标就是使期望词对应的条件概率尽可能大。
相比单纯的前馈神经网络,隐状态的传递性使得RNN语言模型原则上可以捕捉前向序列的所有信息(虽然可能比较弱)。通过在整个训练集上优化交叉熵来训练模型,使得网络能够尽可能建模出自然语言序列与后续词之间的内在联系。
神经网络语言模型小结:神经网络语言模型(NNLM)通过构建神经网络的方式来探索和建模自然语言内在的依赖关系。尽管与统计语言模型的直观性相比,神经网络的黑盒子特性决定了NNLM的可解释性较差,但这并不妨碍其成为一种非常好的概率分布建模方式。
- 优点:(1) 长距离依赖,具有更强的约束性;(2) 避免了数据稀疏所带来的OOV问题;(3) 好的词表征能够提高模型泛化能力。
- 缺点:(1) 模型训练时间长;(2) 神经网络黑盒子,可解释性较差。
语言模型评价指标
信息论中常采用**相对熵(relative entropy)**来衡量两个分布之间的相近程度。对于离散随机变量X,熵、交叉熵以及相对熵的定义分别如下:
H ( p ) = − ∑ i p ( x i ) log p ( x i ) H(p)=-\sum_ip(x_i)\log p(x_i) H(p)=−i∑p(xi)logp(xi)
H ( p , q ) = − ∑ i p ( x i ) log q ( x i ) H(p,q)=-\sum_ip(x_i)\log q(x_i) H(p,q)=−i∑p(xi)logq(xi)
D ( p ∣ ∣ q ) = H ( p , q ) − H ( p ) = ∑ i p ( x i ) log p ( x i ) / q ( x i ) D(p||q)=H(p,q)-H(p)=\sum_{i}p(x_i)\log p(x_i)/q(x_i) D(p∣∣q)=H(p,q)−H(p)=i∑p(xi)logp(xi)/q(xi)
其中, p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)都是对随机变量概率分布的建模。
假定 p p p是样本的真实分布, q q q是对其的建模。因为真实分布的熵 H ( p ) H(p) H(p)值是确定的,因此优化相对熵 D ( p ∣ ∣ q ) D(p||q) D(p∣∣q)等价于优化交叉熵 H ( p , q ) H(p,q) H(p,q)。这里有个小细节是 H ( p , q ) ≥ H ( p ) H(p,q)\ge H(p) H(p,q)≥H(p)恒成立.
对于自然语言序列 W = w 1 , w 2 , . . . , w N W=w_1,w_2,...,w_N W=w1,w2,...,wN,可以推导得到对每个词的平均交叉熵为: H ( W ) = − 1 N log P ( w 1 , w 2 , . . . , w N ) H(W)=-\frac{1}{N}\log P(w_1,w_2,...,w_N) H(W)=−N1logP(w1,w2,...,wN)
显然,交叉熵越小,则建模的概率分布越接近真实分布。交叉熵描述的是样本的平均编码长度,虽然物理意义很明确,但是不够直观。因此,在此基础上,我们定义困惑度(perplexity):
P r e p l e x i t y ( W ) = 2 H ( W ) = 1 P ( w 1 , w 2 , … , w N ) N Preplexity(W) = 2^{H(W)} = \sqrt[N]{\frac{1}{ P(w_1,w_2,\ldots,w_N)}} Preplexity(W)=2H(W)=NP(w1,w2,…,wN)1
由公式可知:困惑度越小,说明所建模的语言模型越精确。
总结
从特性上可以将 n-gram 语言模型看作是基于词与词共现频次的统计,而神经网络语言模型则是给每个词分别赋予分布式向量表征,探索它们在高维连续空间中的依赖关系。实验证明,神经网络的分布式表征以及非线性映射更加适合对自然语言进行建模。
语言模型在机器翻译和语音识别中的应用。基于贝叶斯定理,这两类应用都可以建模为如下形式
P ( y ∣ x ) = P ( x ∣ y ) P ( y ) P ( x ) P(y|x)=\frac{P(x|y)P(y)}{P(x)} P(y∣x)=P(x)P(x∣y)P(y)
从贝叶斯概率的角度出发,可以将语言模型 P ( y ) P(y) P(y) 看作为一种先验知识,从而指导最终结果选择。
参考资料
[1] 自然语言处理中N-Gram模型介绍
[2] NLP基础:n-gram语言模型和神经网络语言模型
[3] nlp自然语言处理之word2vec–cbow和skip gram讲解
[4] 通俗理解n-gram语言模型
[5] 宗成庆老师的《统计自然语言处理 第二版》
[6] A Neural Probabilistic Language Model
[7] 深入理解语言模型 Language Model
