Co-Scale Conv-Attentional Image Transformers
Co-Scale Conv-Attentional Image Transformers
- 一、引言
- 二、实现方法
-
- (一)、Conv-Attention Module
- 三、Co-Scale Conv-Attentional Transformers
-
- (一)、Co-Scale串行块
- (二)、Co-Scale并行块
- (三)、Model Architecture
- 四、实验
-
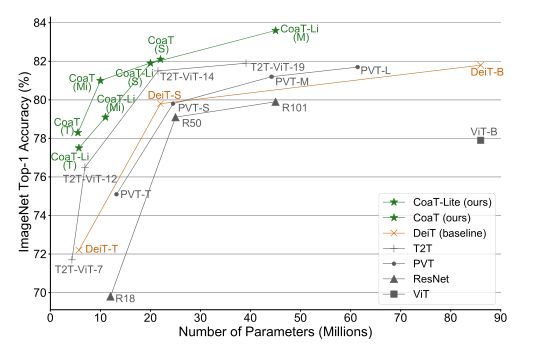
- (一)、图像分类
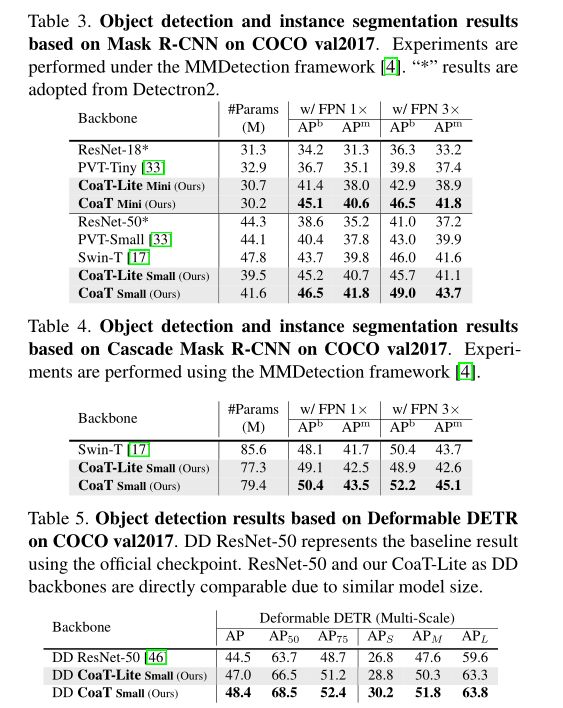
- (二)、目标检测和语义分割
- (三)、消融实验
论文地址: https://openaccess.thecvf.com/content/ICCV2021/papers/Xu_Co-Scale_Conv-Attentional_Image_Transformers_ICCV_2021_paper.pdf
code: https://github.com/mlpc-ucsd/CoaT
一、引言
在本文中,作者提出了一种基于共尺度(Co-scale)的图像分类器,它配备了共尺度和常规注意力机制。首先,共尺度机制在单个尺度上保持Transformers编码器分支的完整性,同时允许在不同尺度上学习的表示有效地相互通信;本文设计了一系列的串并联块来实现共尺度机制。其次,设计了一种卷积注意力机制,通过在分解注意力模块实现一个相对位置嵌入公式,并实现了一种高效的类卷积。CoaT赋予Transformers丰富的多尺度和上下文建模能力。
尽管卷积和自注意操作都执行加权和,但它们的权重计算方式不同:在CNN中,权重在训练期间学习,但在测试期间固定;在自注意机制中,权重是根据每对令牌之间的相似性或亲和度动态计算的。因此,自注意机制中的自相似操作提供了可能比卷积操作更自适应和更通用的建模手段。此外,位置编码和嵌入的引入为Transformers提供了额外的灵活性,可以对固定输入结构之外的空间配置建模。
在开创性的DEtection TRansformer (DETR)算法中,使用Transformer进行目标检测和语义分割,但DETR仍然使用CNN主干提取图像的基本特征。最近,人们开始努力从头开始构建图像分类器,这些分类器都是基于Transformers。虽然基于transformer的图像分类器已经有了十分优异结果,但性能和设计与成熟的CNN模型仍然存在差距。例如,将输入图像划分为固定patch大小的单个网格。在本文中,作者通过引入两种对基于transformer的图像分类器具有实际意义的机制,开发了共尺度常规注意力机制的图像transformer (CoaT):
1、本文引入了一种共尺度机制,通过在不同尺度上保持编码器分支,同时吸引跨尺度的注意力。开发了串行和并行两种构建块,实现了细到粗、粗到细、跨尺度的图像建模。
2、设计了一个卷积注意力模块,在分解注意模块中使用卷积实现相对位置嵌入,与Transformers的普通自注意层相比,计算效率显著提高。
共尺度常规Transformers(CoaT)的开发是由两个结果驱动的:
(1)多尺度建模通常会增强表示学习的能力;
(2)相对位置编码与卷积之间的内在联系使得使用类卷积运算进行有效的自注意成为可能。
因此,实验中显示的CoaT模型的卓越性能来自于我们在Transformers中的两个新设计:(1)允许跨尺度相互作用的共尺度机制;(2) conv -attention模块,实现高效的自注意操作。
Co-Scale vs. Multi-Scale:多尺度方法在计算机视觉领域有着悠久的历史。卷积神经网络自然地实现了细到粗的策略。U-Net除标准的细到粗路径外,还加强了额外的粗到细路径;HRNet通过在整个卷积层中同时保持细尺度和粗尺度,进一步增强了建模能力。图像Transformers的不同尺度的层是串联的,但只是执行细到粗的策略。本文提出的共尺度机制与现有方法的不同之处在于响应的计算方式和相互交互方式:CoaT由一系列高度模块化的串行和并行块组成,使标记化表示上的细到粗、粗到细和跨尺度信息能够起到全局注意力的作用。共尺度模块中跨不同尺度的联合注意机制提供了超越现有视觉Transformers的增强建模能力。
Conv-Attention vs. Attention:纯基于注意力的模型已被引入视觉领域。用自注意模块取代类似resnet架构中的卷积,以实现更好的局部和非局部关系建模。最近有研究通过引入卷积来增强注意机制。LambdaNets为全局上下文建模引入了一种有效的自注意力替代方法,并利用卷积实现了局部上下文建模中的相对位置嵌入。CPVT设计二维深度卷积作为自注意后的条件位置编码。在我们的卷积注意力机制中:(1)采用有效因子化注意;(2)将其扩展为深度卷积相对位置编码和卷积位置编码的组合。
二、实现方法
重温缩放点积注意力:
原Transformers的缩放点积注意公式为:
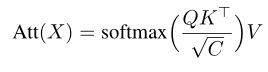
至于Transformers这个公式怎么来的,可以查看此篇博客: Transformer详解
上式中的softmax由于其 O ( N 2 ) O(N^2) O(N2)空间复杂度和 O ( N 2 C ) O(N^2C) O(N2C)时间复杂度,对于高分辨率图像(即N远远大于C)来说是无法承受的。为了减少序列的长度,ViT通过补丁而不是像素来标记图像。然而,粗分割(例如16×16补丁)限制了在每个补丁中建模细节的能力。为了解决这一困境,本文提出了一种协同尺度机制,在有效的传统注意模块的帮助下,提供了增强的多尺度图像表示,降低了高分辨率图像的计算复杂性。
(一)、Conv-Attention Module
因子化注意机制:受最近关于自注意力线性化的工作的启发,通过使用两个函数 φ ( ⋅ ) , ψ ( ⋅ ) : R N × C → R N × C ′ φ(·),ψ(·):R^{N×C}→R^{N×C^{'}} φ(⋅),ψ(⋅):RN×C→RN×C′来近似softmax注意映射,并一起计算第二次矩阵乘法(键和值):
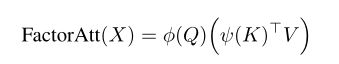
分解得到 O ( N C ′ + N C + C C ′ ) O(N C^{'} + N C + CC^{ '}) O(NC′+NC+CC′)空间复杂度(包括 ϕ ( ⋅ ) 、 ψ ( ⋅ ) ϕ(·)、ψ(·) ϕ(⋅)、ψ(⋅)和矩阵乘积中间步骤的输出)和 O ( N C C ′ ) O(N CC^{ '}) O(NCC′)时间复杂度,其中两者都是序列长度N的线性函数。作者根据LambdaNets开发了分解注意力机制,其中φ为恒等函数,ψ为softmax:
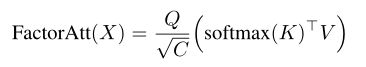
其中softmax(·)以元素的方式应用于序列中的令牌,投影通道 C ′ = C C^{ '} = C C′=C。在LambdaNets中,比例因子 1 / √ C 1/√C 1/√C隐式地包含在权重初始化中,而分解注意力显式地应用比例因子。这种分解的注意力包含 O ( N C + C 2 ) O(N C + C^2) O(NC+C2)空间复杂度和 O ( N C 2 ) O(N C^2) O(NC2)时间复杂度。
卷积作为位置编码:分解注意力模块减轻了原始的点积注意力的计算负担。但是,因为先计算 L = s o f t m a x ( K ) T V ∈ R C × C L = softmax(K)^TV∈R^{C×C} L=softmax(K)TV∈RC×C,所以L可以被视为查询映射Q中每个特征向量的全局数据相关线性变换。这表明,如果有来自Q的两个查询向量 q 1 , q 2 ∈ R C q1, q2∈R^C q1,q2∈RC,并且q1 = q2,那么它们对应的自注意力输出是相同的:
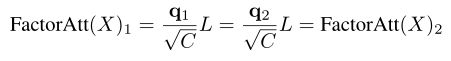
没有位置编码,Transformers仅由线性层和自注意力模块组成。因此,令牌的输出依赖于相应的输入,而不知道其局部附近特征的任何差异。这一特性不利于视觉任务,如语义分割(例如天空和海洋中相同的蓝色斑块被分割为同一类别)。为了实现视觉任务,ViT和DeiT在输入中插入了绝对位置嵌入,这可能会限制局部令牌之间的建模关系。相反,我们可以集成一个相对位置编码 P = p i ∈ R C , i = − M − 1 2 , … , M − 1 2 P = {p_i∈R^C, i =\frac{−M−1}{2},…, \frac{M−1}{2}} P=pi∈RC,i=2−M−1,…,2M−1,取窗口大小为M的相对注意图 E V ∈ R N × C EV∈R^{N×C} EV∈RN×C;在注意力表述中,如果将令牌视为一维序列:
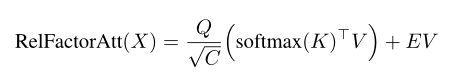
其中编码矩阵 E ∈ R N × N E∈R^{N×N} E∈RN×N有元素:
![]()
其中, 1 ( i , j ) = 1 { ∣ j − i ∣ ≤ ( M − 1 ) / 2 } ( i , j ) 1(i, j) = 1_{\{|j−i|≤(M−1)/2\}}(i, j) 1(i,j)=1{∣j−i∣≤(M−1)/2}(i,j)为指标函数。每个元素 E i j E_{ij} Eij表示窗口M中查询 q i q_i qi到值 v j v_j vj的关系, ( E V ) i (EV)_i (EV)i聚合了查询 q i q_i qi的所有相关值向量。但EV项仍然需要 O ( N 2 ) O(N^2) O(N2)空间复杂度和 O ( N 2 C ) O(N^2C) O(N2C)时间复杂度。在CoaT中,建议通过将查询中的每个通道、位置编码和值向量视为内部头部,将EV项简化为关系式 E V ^ \hat{EV} EV^。因此,对于每个内部头l,我们有:
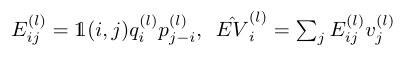
我们可以使用1-D深度卷积来计算 E V ^ \hat{EV} EV^:

其中o为Hadamard乘积。在视觉Transformers中,我们有两种类型的令牌,类(CLS)令牌和图像令牌。因此,使用二维深度卷积(窗口大小M ×M,核权值P),并仅将其应用于重塑后的图像令牌(即 Q i m g , V i m g ∈ R H × W × C Q^{img}, V ^{img}∈R^{H×W ×C} Qimg,Vimg∈RH×W×C分别来自Q, V):
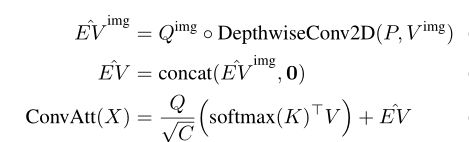
基于以上的推导,深度卷积可以看作是相对位置编码的一种特殊情况。
卷积相对位置编码与其他相对位置编码。通常引用的相对位置编码适用于标准的缩放点积注意设置,因为编码矩阵E与注意图中的softmax分数输出结合在一起,原LambdaNets的主要结果是使用三维卷积直接计算EV,并将查询和键的通道减少到 C K < C C_K < C CK<C处的C_K,但其空间复杂度为 O ( N C C K ) O(N CC_K) O(NCCK),时间复杂度为 O ( N C C K M 2 ) O(N CC_KM^2) O(NCCKM2),当通道大小为 C K 时, C C_K时,C CK时,C计算量较大。LambdaNets的最新更新在资源受限的情况下提供了一个具有深度卷积的高效变体。我们的因式注意力仅用 O ( N C ) O(NC) O(NC)空间复杂度和 O ( N C M 2 ) O(NCM^2) O(NCM2)时间复杂度来计算EV,目的是达到更好的效率。
卷积位置编码:将卷积相对位置编码的思想推广到一般的卷积位置编码情况。卷积相对位置编码对查询和值之间的局部基于位置的关系进行建模。与大多数图像Transformers使用的绝对位置编码类似,我们希望将位置关系直接插入到输入图像特征中,以丰富相对位置编码的效果。在每个卷积注意模块中,对输入特征X进行深度卷积,并按照标准的绝对位置编码方案(见下图下半部分)将得到的位置感知特征连接回输入特征,这类似于CPVT中条件位置编码的实现。
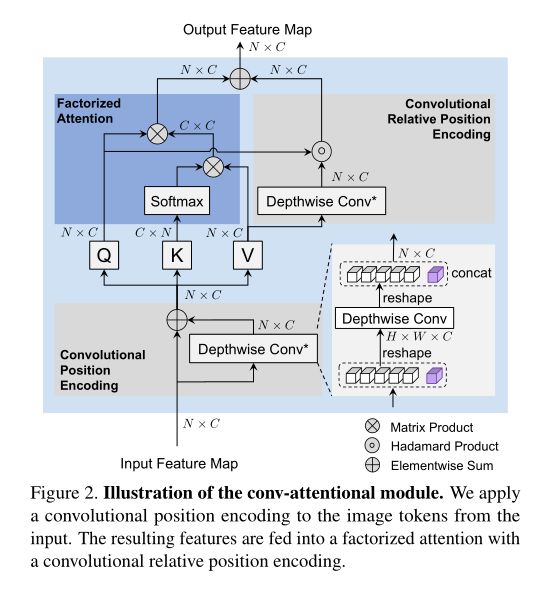
CoaT和CoaT- lite共享同一尺度内串行模块和并行模块的卷积位置编码权值和卷积相对位置编码权值。对于卷积位置编码,将卷积核大小设置为3。对不同注意力头的图像特征分别设置卷积核大小为3,5,7进行卷积相对位置编码。CPVT的工作探索了将卷积作为条件位置编码的使用,方法是在单一尺度下(H/16 × W/16)的前馈网络之后插入卷积。本文的工作重点是将卷积应用于相对位置编码和具有因子注意力的一般位置编码。最后的convtional -attention模块如上图所示:对输入的图像标记应用第一个卷积位置编码。然后,将其输入ConvAtt(·),包括因子注意和卷积相对位置编码。得到的映射被用于后续的前馈网络。
三、Co-Scale Conv-Attentional Transformers
所提出的共尺度机制旨在将细到粗、粗到细和跨尺度信息引入图像Transformers。在这里,本文描述CoaT体系结构中的两种类型的构建块,即串行块和并行块,以便建模多个尺度并启用协同尺度机制。
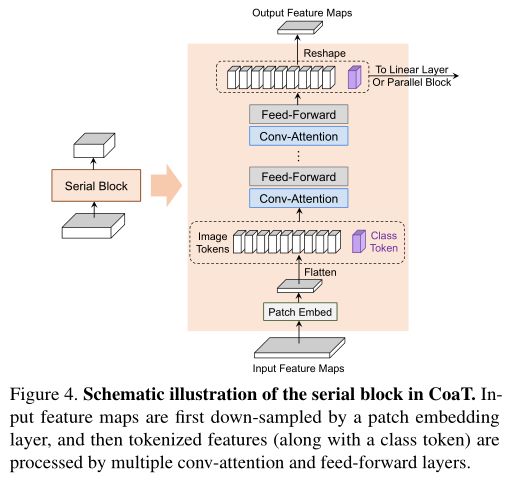
(一)、Co-Scale串行块
串行块(如上图所示)以降低分辨率的方式对图像表示进行建模。在典型的串行块中,首先使用补丁嵌入层按一定比例向下采样输入特征映射,并将减少的特征映射压扁为图像标记序列。
然后,将图像标记与一个额外的CLS标记(用于执行图像分类的专用向量)连接起来,并应用多个常规注意模块来学习图像标记和CLS标记之间的内部关系。最后,将CLS令牌与图像令牌分离,并将图像令牌重塑为下一个串行块的2-D特征映射。
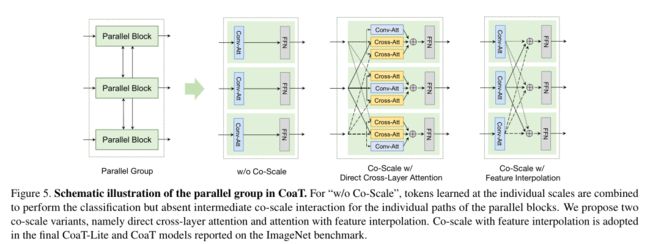
(二)、Co-Scale并行块
在每个并行组中的并行块之间实现了共尺度机制(如上图所示)。在典型的并行组中,有来自不同尺度的串行块的输入特征序列(图像令牌和CLS令牌)。为了在平行组中实现细到粗、粗到细和跨尺度的交互,开发了两种策略:(1)直接跨层注意;(2)注意特征插值。为了获得更好的经验性能,本文采用了带有特征插值的注意算法。两种策略的有效性见实验。
直接跨层注意力。在直接跨层注意力中,从每个尺度的输入特征中形成查询、键和值向量。对于同一层内的注意力,使用convc -attention(图2)与当前规模的查询、键和值向量。为了在不同的层之间进行注意力,向下采样或向上采样键和值向量来匹配其他尺度的分辨率,从而实现细到粗以及粗到细的交互。然后,执行交叉注意力,这将使用来自当前尺度的查询和来自另一个尺度的键和值扩展convc -attention。最后,将集中注意和交叉注意的输出相加,并应用一个共享前馈层。通过直接的跨层注意,跨尺度信息以交叉注意的方式融合。
注意特征插值。我们不再直接进行跨层注意,而是用特征插值来表示注意。首先,利用独立的卷积注意模块对不同尺度的输入图像特征进行处理;然后,从每个尺度下采样或上采样图像特征,使用双线性插值来匹配其他尺度的尺寸,或者对自己的尺度保持相同。属于同一尺度的特征在并行组中求和,并进一步传递到共享前馈层。这样,下一步的常规注意模块就可以在当前步骤的特征插值的基础上学习跨尺度信息。
(三)、Model Architecture
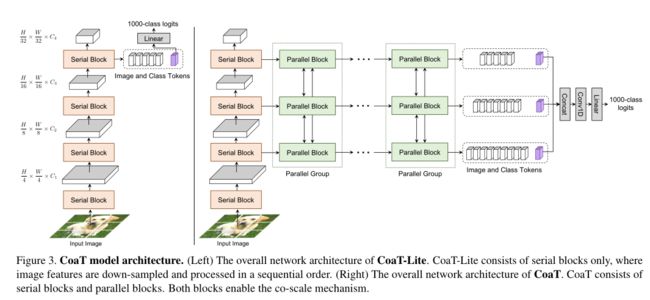
CoaT-Lite。CoaT-Lite,上图图(左),处理输入图像与一系列串行块遵循细到粗金字塔结构。给定一个输入图像 I ∈ R H × W × C I∈R^{H×W ×C} I∈RH×W×C,每个串行块对图像特征进行低分辨率下采样,得到四个分辨率的序列。在CoaT-Lite中,在最后一个串行块中获取CLS令牌,并通过基于CLS令牌的线性投影层进行图像分类。
CoaT:CoaT模型,如上图(右)所示,由串行和并行块组成。一旦从串行块中获得多尺度特征映射{F1, F2, F3, F4},将F2, F3, F4和相应的CLS令牌传递到具有三个独立并行块的并行组中。为了使用CoaT进行分类,将CLS聚合在一起。
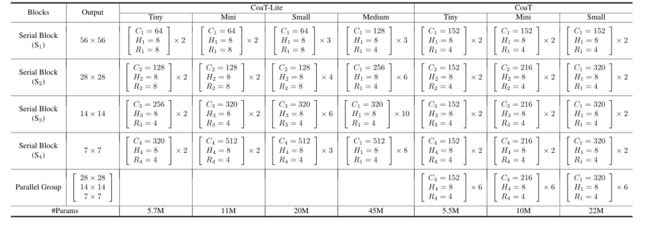
模型变体:在本文中,探索了几种不同型号的CoaT和CoaTLite,即Tiny, Mini, Small和Medium。体系结构细节如下表所示。例如,微型模型表示那些有5M参数预算约束的模型。具体来说,这些微型模型有四个串行模块,每个模块有两个常规注意模块。在CoaT-Lite Tiny架构中,注意力层的隐藏尺寸在后面的块中增加。CoaT Tiny设置并行组中注意层隐藏维数相等,并在六个并行组中执行共标机制。迷你、小型和中型模型遵循相同的架构设计,但增加了嵌入尺寸,增加了块内常规注意模块的数量。
四、实验
(一)、图像分类
(二)、目标检测和语义分割
(三)、消融实验
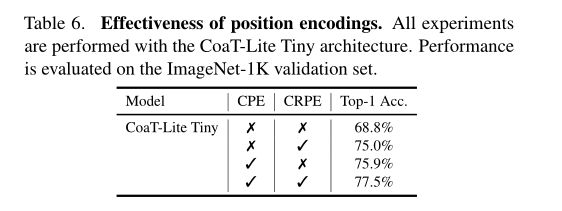
位置编码的有效性。在下表中,研究了卷积相对位置编码(CRPE)和卷积位置编码(CPE)在卷积注意力模块中组合的有效性。CoaT-Lite没有任何位置编码导致性能很差,这表明位置编码对于Transformers来说是必不可少的。使用CRPE或CPE的CoaT-Lite变体有很大的改善,CRPE和CPE的组合导致了最好的性能(77.5%的top-1精度),使两种位置编码方案互补而不是冲突。
Co-Scale的有效性。在下表中,给出了CoaT中两种共尺度变量,直接交叉注意和带有特征插值的注意的性能结果。还报告了无co-scale的CoaT作为基线。与无co-scale的CoaT相比,插值在图像分类和目标检测(Mask R-CNN w/ FPN 1×)上都有了性能的提高。与直接跨层注意相比,特征插值注意具有较低的计算复杂度和较高的精度。
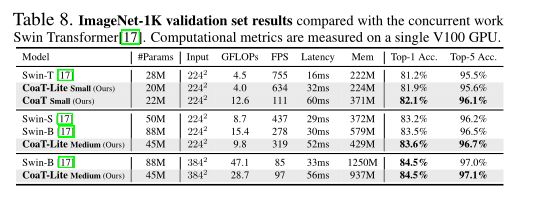
计算成本。在下表中报告了FLOPs、FPS、延迟和GPU内存使用情况。总而言之,CoaT模型比类似大小的Swin transformer获得了更高的精度,但CoaT模型通常具有更大的延迟/ flop。目前CoaT中的并行组对计算的要求更高,可以通过减少高分辨率并行块并在未来的协同尺度机制中重用它们的特征映射来缓解这一问题。CoaT中的延迟开销可能是由于操作(例如。层,位置编码,上采样/下采样)不是并行运行的。