基于采样的路径规划算法总结
基于采样的路径规划算法总结
路径规划算法大致可以分为两类,一类是基于搜索的规划,另一类就是本文将要涉及的基于采样的规划。一般而言,基于搜索的规划(如A*)通常是运行在栅格地图上的。当栅格的分辨率越高时,算法搜索的路径就会越优。
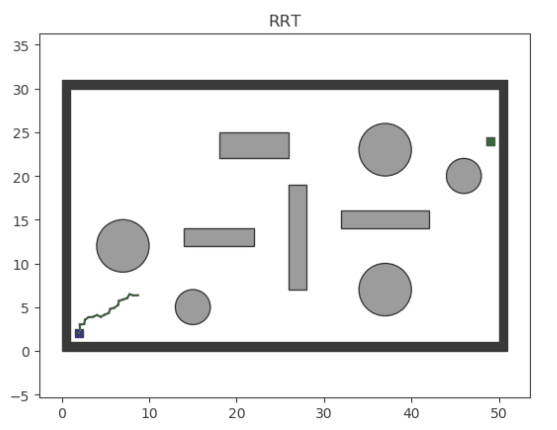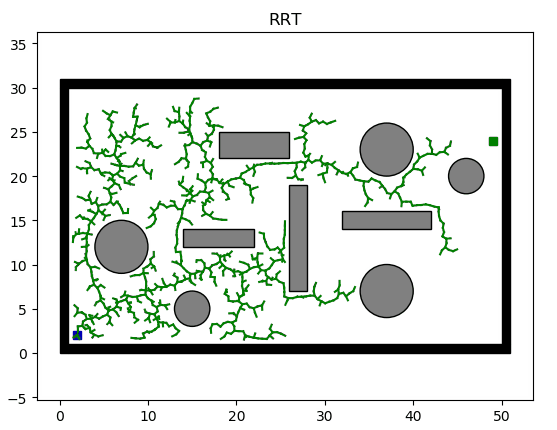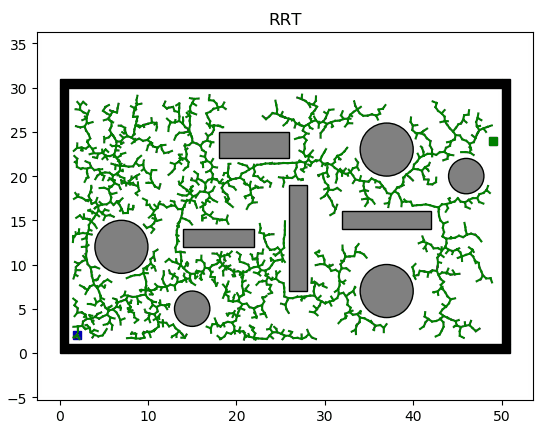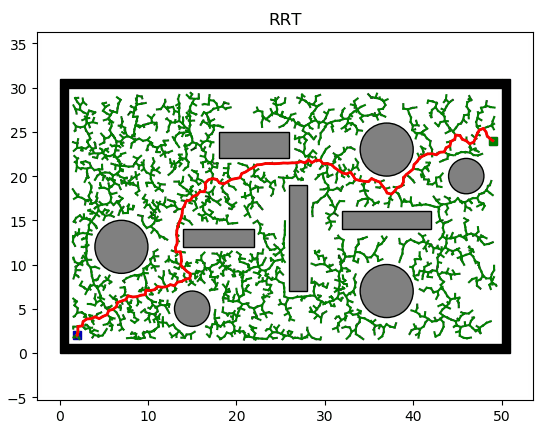
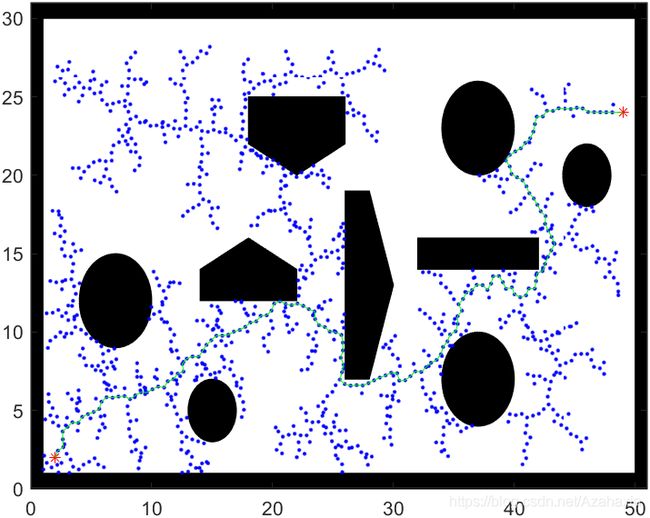
还有一类算法是基于采样的,主要就是RRT和它的变种算法。这类算法的核心在于随机采样,从父节点开始,随机在地图上生成子节点,连接父子节点并进行碰撞检测,若无碰撞,就扩展该子节点。就这样,不断地随机扩展样本点,直到生成一条连接起点和终点的路径。如下图所示,RRT算法的扩展图与盘根错节的树枝十分相似。
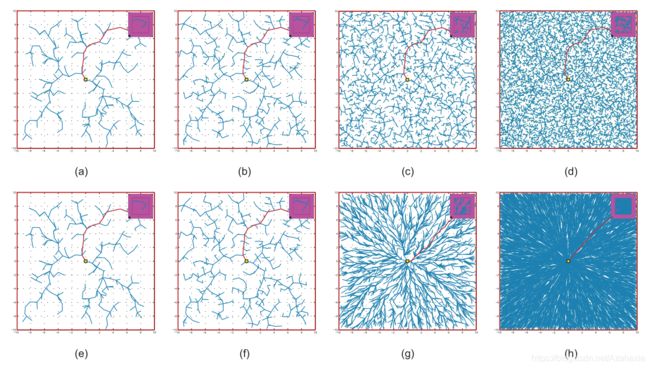
RRT算法是一种快速搜索算法,但是它却是以牺牲最优性为代价的。RRT算法搜索到的路径往往不是最优路径。为了解决这个问题,后来出现了RRT* ,使得RRT拥有了渐进最优的特性。如下图所示,随着节点数量的增加,RRT* 会不断地优化路径,最终趋近于最优。
虽然 RRT* 拥有了在理论上可以找到最优路径的能力,但这种向最优逼近的速度并不快。因此,为了提高 RRT* 的收敛速度,Informed-RRT* 出现了,提高了初始路径向最优路径的收敛速度。
Informed-RRT* 的主要思路是在于椭圆的一个特性:椭圆上的点到椭圆两个焦点的距离之和相同,而椭圆外的点到椭圆两个焦点的距离之和大于前者,内点则反之。
当Informed-RRT* 第一次找到一条可用路径时,就会根据该路径长度画出一个椭圆,该椭圆上的点到两焦点的距离就是该路径长度。因此,为了优化当前路径,算法只需要在该椭圆内扩展样本即可。每当找到一条更短路径,椭圆的范围也会随着变小,如下图所示。
本质上,Informed-RRT* 提供了一个向最优路径优化的方向,从而极大地提高它的收敛速度。这种优化方法使得RRT的样本不再是 均匀(uniform) 的随机扩展,而是 有偏向(bias) 的随机扩展。
下面是我会详细介绍RRT、RRT-CONNECT、RRT* 、Informed-RRT* 算法。算法是使用MATLAB实现的,程序源码放在这里。
1.RRT
关于RRT的编程实现比较简单,但我初次编程时仍然有很多需要注意的地方。首先理一理RRT的整体执行流程:
-
初始化节点扩展的步长 s t e p step step。初始化VERTEX表格,该表格用于储存每次随机生成的且满足条件的节点,然后把起点加入到V表中;
-
以整张地图为范围,随机生成一组坐标,以此作为一个新节点 v r a n d v_{rand} vrand。然后根据V表,从中找到离 v r a n d v_{rand} vrand最近的节点作为它的父节点 v n e a r e s t v_{nearest} vnearest;
-
计算 v r a n d v_{rand} vrand与 v n e a r e s t v_{nearest} vnearest的距离,取与步长相比较后的最小值,防止两节点之间的距离过长;
dist = min([norm(new_vertex-near_vertex),step_len]); % 两节点之间的距离 theta = atan2(new_node.ny-near_node.ny,new_node.nx-near_node.nx); % 两节点之间的方向 new_node.nx = near_node.nx + dist*cos(theta); new_node.ny = near_node.ny + dist*sin(theta); -
对于edge( v r a n d v_{rand} vrand, v n e a r e s t v_{nearest} vnearest)进行碰撞检测,若满足要求,则将该节点加入到V表中。反之,则返回第二步;
-
判断 v r a n d v_{rand} vrand与终点的距离,若其小于步长并且之间无碰撞,则把终点加入到V表中,并设置 v r a n d v_{rand} vrand为终点的父节点,然后根据父节点提取出一条可行路径。反之,则返回第二步。
观察代码和可视化图像,可以发现,RRT算法并没有设置任何优化路径的程序。当RRT发现一条可连接起点与终点的可行路径时,就直接把这条路径作为最终解。也就是说,RRT只能找到一个可行解,但不保证该解就是最优解。
2.RRT-CONNECT
观察可视化图像,可以发现RRT的均匀采样(uniform sample)很没有效率,会把大部分的采样点放在无意义的区域。如果我们可以缩小这个区域,那么就可以极大提高算法寻径的效率,这也就是所谓的偏置采样(bias sample)。
RRT-CONNECT为了提高RRT算法的效率,做出了两点改进:
The method is based on two ideas: the Connect heuristic that attempts to move over a longer distance, and the growth of RRTs from both q i n i t q_{init} qinit and q g o a l q_{goal} qgoal.
- 采用贪婪策略进行采样,算法会尝试往距离更远的地方移动;
- 采用双向生长,即起点和终点均作为生长树的起点。
关于第一点可能比较难以理解。简单来说,因为该算法是双向生长的,当两个树的某两个节点之间存在可生长空间(即不会与障碍物碰撞)时,算法会优先在这两个节点之间扩展新节点。这样就可以让两个生长树快速相交。
这里主要说明RRT-CONNECT与RRT算法不同的地方。首先,由于前者是双向生长的,因此需要两个VERTEX表格,用于储存从起点和从终点扩展的节点。接下来,详细介绍RRT-CONNECT扩展节点的过程:
- 首先,在地图范围内随机确定一个节点 v r a n d v_{rand} vrand,然后找到新节点与V1表(从起点开始)中所有节点的最近节点作为 v n e a r e s t v_{nearest} vnearest;
- 由于刚开始V1表中只有起点,若两点之间无碰撞,则会从起点附近扩展出一个新节点 v n e w v_{new} vnew(规范化距离后的 v r a n d v_{rand} vrand);
- 接下来,算法会从V2表(从终点开始)中找到与 v n e w v_{new} vnew最近的节点 v n e w 2 v_{new2} vnew2,同样V2表中只有终点,当两点无碰撞时,会从终点附近扩展出一个新节点 v n e w 2 v_{new2} vnew2(规范化);
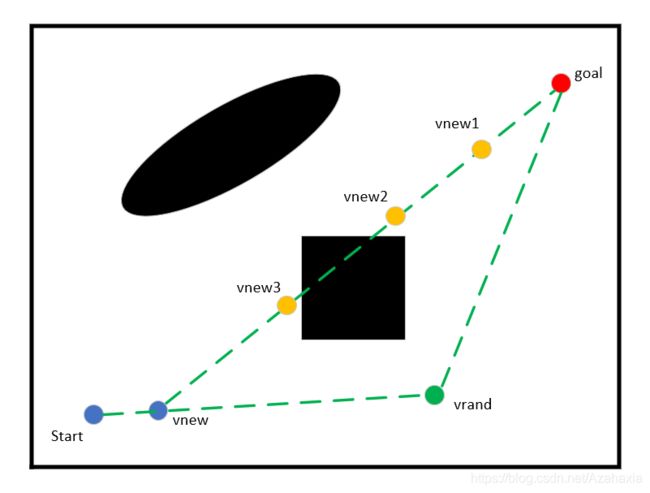
- 此时,算法判断节点 v n e w v_{new} vnew与 v n e w 2 v_{new2} vnew2之间存在可扩展的空间。于是不再随机扩展节点,而是从这两点之间扩展节点。具体操作就是以 v n e w 2 v_{new2} vnew2为起点,朝 v n e w v_{new} vnew的方向以一定步长扩展新节点 v n e w 3 v_{new3} vnew3,若节点 v n e w 2 v_{new2} vnew2与 v n e w 3 v_{new3} vnew3之间仍然无碰撞,则继续扩展下一个节点,直到节点 v n e w v_{new} vnew与 v n e w i v_{newi} vnewi接触或与障碍物碰撞才结束这个贪婪扩展过程。
如下图,当节点扩展到 v n e w 3 v_{new3} vnew3时, v n e w 3 v_{new3} vnew3与 v n e w 2 v_{new2} vnew2之间与障碍物碰撞,故放弃节点 v n e w 3 v_{new3} vnew3并结束贪婪扩展的过程。在第一次扩展结束后,交换两个V表的位置,即下一次扩展时把V1表的地方用V2表替换,把V2表的地方用V1表替换。如此反复,直到找到两个生长树相连。
3.RRT*
RRT-CONNECT通过贪婪生长和双向生长技术极大提高了RRT寻找可行路径的速度,但是仍然没有考虑如何去优化可行解。RRT* 弥补了这个问题,它使得RRT算法获得了渐进最优的能力,即随着采样点数量的增加,算法获得的路径会逐渐向最优路径靠拢。
RRT* 是如何实现这一功能的呢?
RRT* 考虑了每一个节点到起点的代价,代价越低就越可能被选择为路径节点。这种方式在基于搜索的路径规划中早已经被广泛使用了。RRT* 寻找初始路径的过程与RRT相同,区别在于前者找到初始路径后程序并没有结束,而是会继续生成采样点并不断更新初始路径。随着样本点的增加,初始路径会逐渐向最优路径靠近。
下面主要描述RRT* 优化初始路径的过程。
-
在地图上随机产生一个样本点 v r a n d v_{rand} vrand,找到最近点 v n e a r e s t v_{nearest} vnearest并经过碰撞检测后,算法会以 v r a n d v_{rand} vrand为圆心、以一定半径生成一个圆形区域,从V表中找到所有在该区域内的节点,若其通过碰撞检测,则将其作为 v r a n d v_{rand} vrand的相邻节点 v n e a r v_{near} vnear。关于半径的计算方式如下:
r = min ( γ R R T ∗ ( ln ( c a r d ( V ) ) c a r d ( V ) ) 1 d , η ) r = \min(\gamma_{RRT*} (\frac{\ln(card(V))}{card(V)})^{\frac{1}{d}}, \eta) r=min(γRRT∗(card(V)ln(card(V)))d1,η)
上式中,V表示节点集合, c a r d ( V ) card(V) card(V)表示集合V的元素个数,也就是节点的数量。d表示构型空间的维数,由于路径规划是在二维空间寻径的,故 d = 2 d=2 d=2。 η \eta η表示RRT的节点扩展步长, γ R R T ∗ \gamma_{RRT*} γRRT∗是一个系数。 -
**从所有相邻节点中,为 v r a n d v_{rand} vrand找到一个父节点。**具体方式是先计算由相邻节点那条路径移动到 v r a n d v_{rand} vrand的代价,即从起点开始的代价( v s t a r t → . . . → v n e a r → v r a n d v_{start} \rightarrow ... \rightarrow v_{near} \rightarrow v_{rand} vstart→...→vnear→vrand)。然后,取最小代价的节点作为 v r a n d v_{rand} vrand的父节点,并且更新 v r a n d v_{rand} vrand的代价;
-
**根据代价修剪(rewire)生长树。**仍然是对相邻节点操作,这次是从 v r a n d v_{rand} vrand开始。需要注意的是此时的 v r a n d v_{rand} vrand已经有父节点了,假设其父节点为 v n e a r 1 v_{near1} vnear1,那么与相邻点的路径应该是 v s t a r t → . . . → v n e a r 1 → v r a n d → v n e a r v_{start} \rightarrow ... \rightarrow v_{near1} \rightarrow v_{rand} \rightarrow v_{near} vstart→...→vnear1→vrand→vnear,若代价小于 v n e a r v_{near} vnear原来的代价,则更新 v n e a r v_{near} vnear的父节点为 v r a n d v_{rand} vrand并更新原代价值。
注:仅比较圆内节点的代价,而不是所有节点的代价,虽然可以减少计算代价,但是也可能会遗漏一些潜在的更好的路径。当然,这个问题只会出现在迭代次数不多时,随着样本点逐渐增多,算法仍然可以找到趋近于最佳路径的结果。
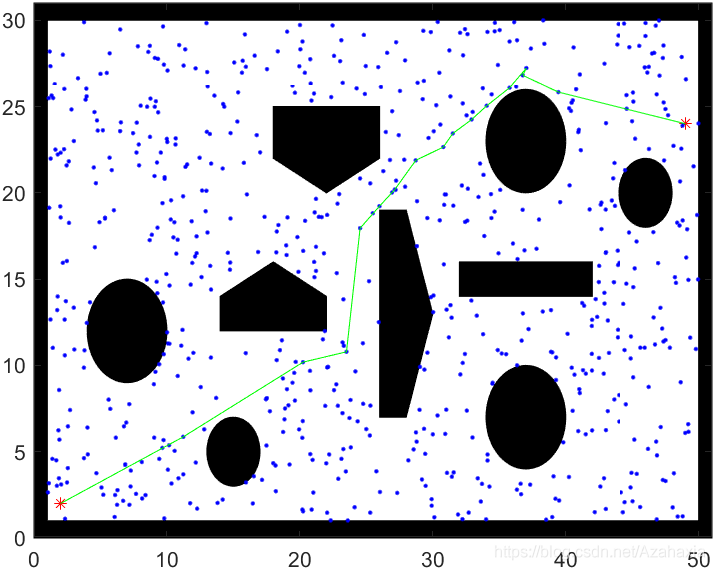
RRT* 在提取路径时与RRT不同,因为生成的路径不止一条,需要根据代价找到代价最小的那条路径作为结果。关键在于要找到代价最小的节点作为终点的父节点。具体寻找过程如下:
- 以终点为圆心、扩展步长为半径生成一个圆形区域,排除所有圆外节点和不通过碰撞检测的圆内节点;
- 计算剩余的所有节点代价,取最小代价的节点作为终点的父节点。
虽然RRT* 根据节点代价会逐渐更新路径,但是它在初始路径的生成和路径的更新过程中,仍然采用了uniform sample的方式进行采样。在实验过程中,我明显的感觉到RRT* 算法向最优路径的收敛速度太慢。虽然理论上,它可以找到最优路径,但是我们仍然希望它向最优路径的收敛速度可以更快一点。
4.Informed-RRT*
关于RRT* 虽然保证了其路径渐进最优的特性,但是当采样环境维数较大时,其向最优路径收敛的速度会变得很慢。这是因为RRT* 是对集合 X X X(地图上的所有点的集合)进行采样的,但是集合 X X X中的大部分点对于路径改善是不起作用的。
但是如果我们可以缩小采样集合的范围,那么是否就可以提高算法的收敛速度呢?
这就是Informed-RRT* 提高收敛速度的方法。它把采样范围缩小到了一个椭圆的范围,算法只要在这个椭圆中采样就可以了。
关于为什么可以这么做就需要先介绍一下启发函数(heuristic function)的作用。假设存在一个启发函数 f ( ⋅ ) f(\cdot) f(⋅),它可以真实描述节点x的最低代价(从起点到终点且经过节点x的最优路径的代价)。但是通常我们是无法知道这个启发函数 f ( ⋅ ) f(\cdot) f(⋅),故只能设计一个函数 f ^ ( ⋅ ) \hat{f}(\cdot) f^(⋅)来估计它。
当然, f ^ ( ⋅ ) \hat{f}(\cdot) f^(⋅)并不是随便设置的,它存在一定的限制,必须满足下式:
∀ x ∈ X , f ^ ( x ) ≤ f ( x ) \forall x \in X, \hat{f}(x)\le f(x) ∀x∈X,f^(x)≤f(x)
也就是说, f ^ ( ⋅ ) \hat{f}(\cdot) f^(⋅)估计的代价不能高于被估计路径的真实代价。这很好理解,假设当前存在一条路径 p p p,其代价为 c c c(该路径是已知的,故可以计算真实代价)。假设在所有可行路径中,代价比它低有m条路径。当我们使用 f ^ ( ⋅ ) \hat{f}(\cdot) f^(⋅)对路径估计代价时,由于不知道其真实代价,必然会导致两种情况:
-
若 f ^ ( ⋅ ) \hat{f}(\cdot) f^(⋅)高估了真实代价,那么就有可能会把原本代价比路径 p p p低的其它路径设置的比 p p p更高了。也就是说在这种启发函数下,比当前路径更优的路径数量会小于m条,这就会存在漏掉最优路径的风险;
X f ^ ⊆ X f X_{\hat{f}} \subseteq X_f Xf^⊆Xf -
若 f ^ ( ⋅ ) \hat{f}(\cdot) f^(⋅)低估了真实代价,那么就有可能会把原本代价比路径 p p p高的其它路径设置的比 p p p更低了。也就是说在这种启发函数下,比当前路径更优的路径数量会大于m条,虽然我们要搜索的范围变大了,但不会漏掉最优路径。
X f ^ ⊇ X f X_{\hat{f}} \supseteq X_f Xf^⊇Xf
注: X f X_f Xf表示可以改善当前路径代价的节点的集合, X f ^ X_{\hat{f}} Xf^是对其的估计。
经过以上分析可知,第二种情况更好。因此,当启发函数满足第二种情况时,可以称启发函数是 “admissible”。满足第二种情况的启发函数很好找,直接用欧几里得距离描述就可以了,因为两点之间直线最短。
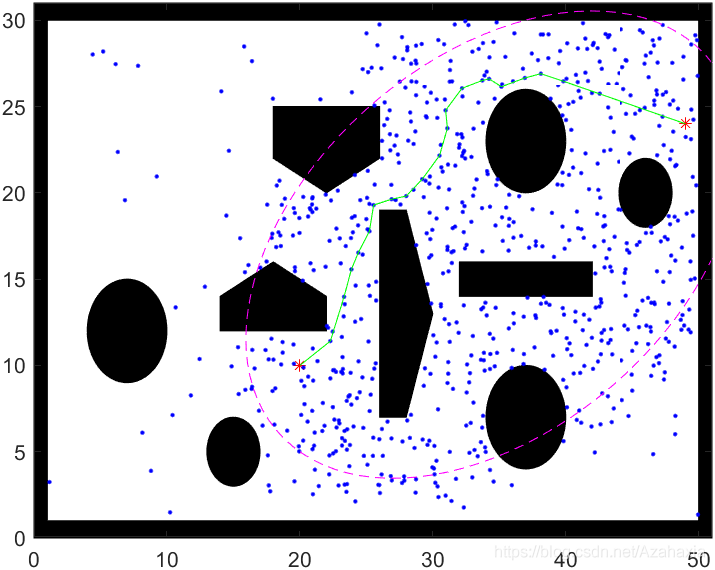
由上可知,可以改善当前路径的节点均存在于集合 X f ^ X_{\hat{f}} Xf^。Informed-RRT* 巧妙的设计了一种启发函数,可以直接从集合 X f ^ X_{\hat{f}} Xf^进行采样,故效率会远高于RRT* 。Informed-RRT* 在找到初始路径后,会根据初始路径的长度设置一个椭圆,如下图所示。
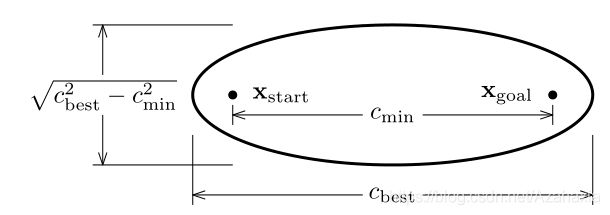
X f ^ = { x ∈ X ∣ ∣ ∣ x s t a r t − x ∣ ∣ 2 + ∣ ∣ x − x g o a l ∣ ∣ 2 ≤ c b e s t } X_{\hat{f}}=\{ x \in X \; | \; ||x_{start}-x||_2 + ||x-x_{goal}||_2 \le c_{best} \} Xf^={x∈X∣∣∣xstart−x∣∣2+∣∣x−xgoal∣∣2≤cbest}
通过把椭圆的长轴设置为初始路径的长度,椭圆外的点到两焦点(起点和终点)的距离之和必然会大于初始路径长度。而若某点的最短路径长度都大于初始路径长度,那么这个点就没有采样的必要了。这样就可以把采样范围缩小到一个椭圆, X f ^ X_{\hat{f}} Xf^就变成了椭圆内的点集,最优路径必然存在于椭圆内。
有了理论基础后,接下来需要解决的就是如何对一个椭圆实现均匀采样。关于这个问题,原论文有详细介绍,这里就不再赘述。
上图是Informed-RRT* 的伪代码,它是直接在RRT* 的基础上修改的,上图中红色标注的就是修改部分。可以发现,修改部分很少,基本上只是修改了采样的部分。