多标签学习与深度森林学习笔记
周志华老师团队Multi-Label Learning with Deep Forest (MLDF)报道很多，各大机器学习平台也都就这篇文章的亮点给出了分析。近日在准备组会报告时较为详细地拜读了一下，也由此简单了解了一下多标签学习的相关内容。
正如论文作者所述，MLDF的最大优势在于：
-
限制模型复杂性以防止过拟合
-
可以根据用户需求进行优化
实验表明，在多个标准数据集（benchmark dataset）上，深度森林在六种多标签学习的评价方法中取得了最佳表现，同时也具有在多标签问题中研究标签之间相关性的能力。
下面就多标签学习问题和深度森林在这一类问题上的应用记录一下学习内容。
1. 多标签学习问题
1.1 问题描述
多标签学习 (Multi-Label Learning) 是与单标签学习 (Single-Label Learning) 相对应的概念。对于单标签学习的问题在生活中非常常见，比如判断一张图片中的动物是猫还是狗。而多标签则是一个样本同时具有多个标签，需要人们同时识别出来，比如一张图片中可以同时有天空、湖水、城堡、天鹅等等。
图片来源：Huang and Zhou, Fast Multi-Instance Multi-Label Learning, PAMI, 2013.
这里要注意的是不要把多标签问题和多类别 (Multi-Class)问题 混淆。多类别问题仍然是单标签的，一个样本只对应一个标签。
现阶段多标签学习主要关注多标签分类问题，对于回归的研究相对较少。多标签分类主要关注一下几个方面：
-
输入一个样本，在全标签集中找到它所对应的标签
-
对于所有相关的标签，根据相关性加以排序
-
探索标签之间的关联 (Label Correlation)
1.2 评价指标
多标签分类的评价方法有很多，MLDF文章中用到了下面的六种指标，如果有兴趣了解更多评价指标的朋友们可以查阅文末参考文献[3]和[4]，里面有较为详尽的介绍（当然其他综述文献中也都有，个人更推荐这两篇），对于不太理解的概念可以多看几种解释，基本都可以弄懂。这里不展开说明了。
表格来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
表格中 m 是样本数量， l 是标签数量， h 表示模型输出结果，上（下）箭头表示指标约大（小）越好。
2. 深度森林(gcForest)模型
由于MLDF是基于深度森林构建的，这里对深度森林模型做简要介绍。深度森林（Paper）是周志华老师团队在2017年提出的。出于好奇专门了解了一下为什么叫"gcForest"。这个名称来源于"multi-Grained Cascade Forest"，是指多粒度级联森林。
正如要了解随机森林就要先了解决策树一样，这里我们先从深度森林最基本的组成单位——预测聚类树（Predictive Clustering Tree (PCT)）开始。PCT的基本思想如下：自顶而下构建一棵树，每次分枝将样本分到各个子节点上，这样PCT构建完成时每个叶子节点就包含了若干个样本，含有多个标签。PCT的构建过程与决策树类似，停止生长、剪枝和其他策略均可相似地应用到PCT上，具体可以参考这篇文章。在测试过程中，一个样本会被分到某个叶子节点上，那么这个样本的标签向量就用这一节点上训练集各个标签的比例来表示，标签向量的每个元素代表这一测试样本属于这个标签的概率。
类似随机森林，多个预测聚类树组成了深度森林的基本模块——基于PCT的随机森林（RF-PCT)，如下图所示。需要注意的是在图中每个样本是单标签的，因此每个样本仅有一种颜色（个人认为图中的形状不同是为了更好地加以区分）。
图片来源：Zhou and Feng, Deep Forest, IJCAI, 2017.
深度森林的结构如下图所示，上面提到的RF-PCT成了深度森林中的单一模块。只是深度森林中模块包括两种类型：普通随机森林（黑色）和完全随机森林（蓝色）。两者的区别在于分枝时特征选取的不同，普通随机森林选取 
个特征（n为样本特征数）作为候选，之后再用gini系数选取最佳的特征进行分枝；而完全随机森林是从n个特征中随机选取一个用于分枝。每个森林包含500棵树。
图片来源：Zhou and Feng, Deep Forest, IJCAI, 2017.
深度森林模型包含两个主要部分：多粒度特征扫描 (Multi-Grained Scanning) 和级联森林 (Cascade Forest)。多粒度扫描是在原始特征的基础上用不同大小的滑窗 (Sliding Window) 提取特征（注意：这里不是卷积操作，和CNN中的滑窗是不同的）。例如对于长度为400的特征的三分类任务，用100长度的滑窗扫描原始特征，可以提取到301个长度为100的特征向量，将这些特征分别放到两类森林中会得到两组结果，每组中包含301个长度为3的输出特征向量，拼接后就得到了3*301*2=1806维的输出特征向量。在上图中的深度森林中，特征扫描分别采用了100、200和300长度的滑窗完成。
级联森林的思想和深度神经网络类似，每一层由若干个（这里为4个）随机森林块组成，包括普通随机森林块和完全随机森林块。样本用上面提到的特征扫描得到的输出特征（记为X）表征，分别输入级联森林的第一层中，输出结果再连接输出特征X输入下一层......经过若干层后，在输出层将结果取平均，得到最终的预测结果。需要注意的是这里使用了三种“粒度”的特征扫描方案，级联森林的每一层是包含三个子层的，相邻两层的各子层采用“一对一”连接，即Level1A连接Level2A。
3. 多标签深度森林模型（MLDF)
3.1 MLDF模型结构
做了一堆铺垫，终于来到了MLDF文章中的模型，其实理解了之前的各个模型这里就会显得很简单，MLDF的结构与gcForest类似，如下图所示，但不同在于没有强调特征扫描（查阅了原文没有明确说明要预先做gcForest里面那样的多粒度特征扫描，应该是都可以），并且融合了两种基于评测指标的优化方案，使模型更优。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
3.2 度量感知特征重用（Measure-aware Feature Reuse）
第一种基于评测指标的优化方案是度量感知特征重用 (以下简称MAFR)，对应模型结构图中 
相关部分。正如原文中所说，MAFR的核心思想是在当前层输出特征的置信度小于阈值时，部分重新使用之前层相对较好的特征来替代当前层特征。算法细节如下图所示，首先选取一个合适的评价指标 M ，获得当前层 t 的输出特征 
后，计算一个阈值 
，对于每个标签（或每个样本），计算其对应的置信度 
，如果置信度小于阈值，则该标签（或样本）对应的特征表示 
(或者 
) 用前一层的特征表示 
(或者 
替代；否则仍使用当前层的输出特征表示
(或者 
)。置信度的计算方法与模型采用的评价指标有关，例如使用hamming loss，置信度可以用每一标签取正/负的正确性来计算，对于预测结果
![p_{.j}=[0.9,0.6,0.4,0.3]](http://img.e-com-net.com/image/info8/664f52dbc1fd475ea33e0fc05ac6efda.gif){kind=small}
，
置信度为
（例子来源于论文）
基于标签的评价指标和基于样本的评价指标可以参考文末的参考文献[4]，有较为详细地讲解。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
关于阈值 的计算的算法如下图所示，对于每个标签或者每个样本，计算其在 
上的置信度，同时根据选定的评价指标 M 计算输出 和真实答案 
的度量 
，若 比 
要差，就把 加入到阈值集合 S 中，根据 S 获得阈值 （比如对 S 中的值取平均）。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
3.3 度量感知层增长（Measure-aware Layer Growth）
第二种基于评测指标的优化方案是度量感知层增长 (以下简称MALG)，MALG算法如下图，简单来说就是设定并初始化一个评价指标 
（比如前面提到的hamming loss），模型每加一层（记为t层）时先计算这一指标 
，如果 优于 则更新 并记录对应层索引 
；如果 在最近三层都没有更新则退出层增长过程；只要没有退出，就在现有模型基础上加一层（来到了t+1层），但注意只要没有更新 ，最佳层索引 L 就不会发生变化。层增长过程结束后模型只取前 L 层，这意味着模型后端那些没有更新 但临时添加的层在最后的深度森林模型中是被删去的。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
4. MLDF实验结果
通过与其他5种多标签学习算法的比较，MLDF在9大标准数据集 (benchmark datasets) 上采用6种评价指标均取得了更好的效果。用于比较的算法分别为：RF-PCT[Kocev et al., 2013], DBPNN[Hinton and Salakhutdinov, 2006; Read et al., 2016], MLFE[Zhang et al., 2018a], RAKEL[Tsoumakas and Vlahavas, 2007], ECC[Read et al., 2011].
文章也分析了度量感知特征重用 (MAFR) 机制对结果的影响，如下图所示。每张子图是一个数据集上的结果，每个顶点代表一种多标签学习的评价指标，越靠近顶点表示这种指标下模型表现越好。图中浅色部分表示深度森林使用MAFR机制的表现，深色部分表示深度森林没有使用MAFR的表现。可以直观的看出MAFR对模型性能提升的作用。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
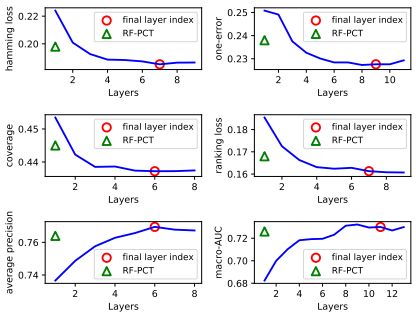
文章还分析了度量感知层增长 (MALG) 机制对结果的影响，如下图所示。评价所用数据集为yeast数据集，每张子图对应于6种评价指标中的一种。实验中当模型达到MALG机制所规定的停止增长条件后，仍增加模型的层数，计算各个指标来测试MALG机制的有效性。红色圈代表MALG机制记录下的最佳层数，可以发现MALG几乎可以确定模型的最佳层数。当层数大于红色圈标记后模型表现几乎不变或者增长不显著。绿色三角形代表RF-PCT的实验结果，在所有评价指标下MLDF表现均优于RF-PCT。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
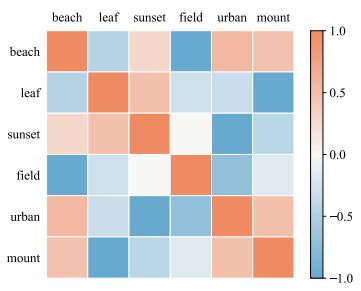
另外文章利用MLDF模型分析了标签的相关性。实验中在模型第一层表示中删除掉某个特定的标签，然后继续训练后面的层，观察结果中其他标签准确性的变化，由此可以分析标签相关性。文章中的分析结果如下图所示。
图片来源：Yang et al., Multi-Label Learning with Deep Forest, aXiv, 2019.
总结一下！MLDF文章的主要贡献为（来自原文）：
-
首先将深度森林方法用于多标签学习
-
MLDF模型在多个标准数据集用多种评价指标的表现优于其他多标签学习模型
5. 多标签学习综述文章
最后给出一些我在准备组会报告时查阅的多标签学习综述文献，内容相近略有不同，供大家参考。
[1] Tsoumakas and Katakis, Multi-label classification: An overview, Int. J. Data Warehousing Mining, 2007.
[2] Tsoumakas et al., Mining multi-label data, Data Mining and Knowledge Discovery Handbook, 2010.
[3] Zhang and Zhou, A Review on Multi-Label Learning Algorithms, IEEE Transactions on Knowledge and Data Engineering, 2014.
[4] Gibajaand Ventura, A Tutorial on Multi-Label Learning, ACM Computing Surveys, 2015.
[5] Xu et al., A Survey on Multi-output Learning. IEEE Transactions on Neural Networks and Learning Systems, 2019.
[6] Borchaniet al., A survey on multi-output regression, Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2015. (这篇是介绍多标签回归问题的，虽然这类问题出现的不多，但有兴趣的朋友们可以关注一下).