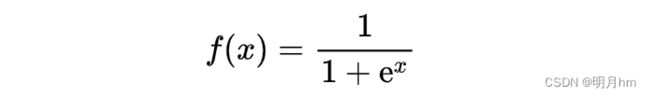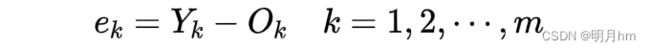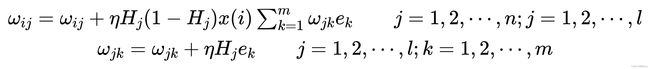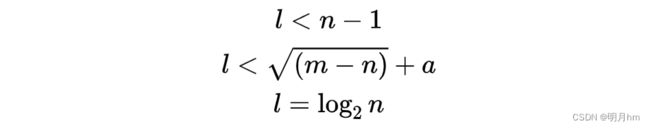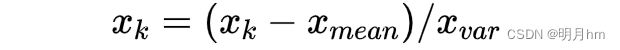《MATLAB神经网络案例分析》学习(一)——BP神经网络基本理论
一、BP神经网络理论基本介绍
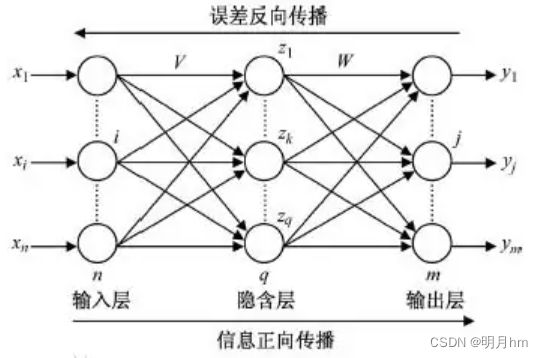
BP(Back Propagation)是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。该网络的主要特点是信号前向传递,误差反向传播。
在前向传递中,输人信号从输人层经隐含层逐层处理直至输出层。每一层的神经元状态只影响下层神经元状态。如果输出层得不到期望输出,则转入反向传播,网络将误差信号沿原来的连接通路反传回来。根据预测误差调整网络权值和阈值,从而使BP神经网络预测输出不断逼近期望输出。BP神经网络的拓扑结构如图所示。
主要思想:对于n个输入学习样本P1,P2,P3...Pn,与之对应的m个输出样本为T1,T2,T3...Tm。学习的目的是利用网络的实际输出A1,A2,A3...Am与目标矢量T,T2,T3...Tm之间的误差来修改其权值,使A和T之间尽可能接近(A与T的误差平方和尽可能小)。BP神经网络是通过连续不断地在相对于误差函数斜率下降的方向上计算网络权值和偏差的变化而逐渐逼近目标的。每一次权值和偏差的变化都与网络误差的影响成正比,并以反向传播的方式传递到每一层的。
可以看出:BP神经网络可以看成一个非线性函数,网络输入值和预测值分别为该函数的自变量和因变量。当输人节点数为n,输出节点数为m时,BP神经网络就表达了从n个自变量到m个因变量的函数映射关系。
二、训练步骤简介:
BP神经网络预测前首先要训练网络,通过训练使网络具有联想记忆和预测能力。BP神经网络的训练过程包括以下几个步骤:
步骤1:网络初始化。根据系统输入输出序列(X,Y)确定网络输入层节点数n,隐含层节点数l,输出层节点数m,初始化输人层、隐含层和输出层神经元之间的连接权值wij,wjk,初始化隐含层阈值α,输出层阈值b,给定学习速率和神经元激励函数。
步骤2:隐含层输出计算。根据输人向量X,输入层和隐含层间连接权值wij,以及隐含层阈值a,计算隐含层输出H。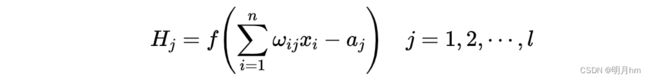
式中,l为隐含层节点数;f为隐含层激励函数。该函数有多种表达形式,本次所选函数为:
其函数图像如下图所示:
步骤3:输出层输出计算。根据隐含层输出H,连接权值wjk和阈值b,计算 BP神经网络预测输出O.
步骤4:误差计算。根据网络预测输出O和期望输出Y,计算网络预测误差e
步骤5:权值更新。根据网络预测误差e更新网络连接权值wij,wjk,式中,![]() 为学习速率。
为学习速率。
步骤6:阈值更新。根据网络预测误差e更新网络节点阈值a,b
步骤7:判断算法迭代是否结束,若没有结束,返回步骤2
三、BP神经网络具体参数确定:
1 输入层、输出层节点数
这两个与实际的应用问题有关,实际问题有几个输入,几个输出,就设置对应数量的节点数。在程序中,输入和输出信号一般使用向量形式进行编辑。
2 隐含层节点数
BP神经网络的隐含层节点数对BP神经网络预测精度有较大的影响:节点数太少,网络不能很好地学习,需要增加训练次数,训练的精度也受影响;节点数太多,训练时间增加,网络容易过拟含。最佳隐含层节点数选择可以参考如下公式:
式中,n为输入层节点数,l为隐含层节点数,m为输出层节点数,a为0-10之间的常数。在实际问题中,一般首先用参考公式来确定节点数的大概范围,然后用试凑法确定最佳的节点数。
3 隐含层层数
增加层数主要可以更进一步的降低误差,提高精度,但同时也使网络复杂化,从而增加了网络权值的训练时间。而误差精度的提高实际上也可以通过增加隐含层中的神经元数目来获得,其训练效果也比增加层数更容易观察和调整。所以一般情况下,应优先考虑增加隐含层中的神经元数。
对于一般的简单数据集,一两层隐藏层就足够了。但对于涉及复杂数据集,则需要额外增加层数。单层神经网络只能用于表示线性分离函数,也就是非常简单的问题,比如分类问题中的两个类可以用一条直线整齐地分开。
- 没有隐藏层:Only capable of representing linear separable functions ordecisions.
仅能够表示线性可分函数或决策 - 隐藏层数=1:Can approximate any function that contains a continuousmapping from one finite space to another.
可以拟合任何“包含从一个有限空间到另一个有限空间的连续映射”的函数 - 隐藏层数=2:Can represent an arbitrary decision boundary to arbitrary accuracy with rational activation functions and can approximateany smooth mapping to any accuracy.
搭配适当的激活函数可以表示任意精度的任意决策边界,并且可以拟合任何精度的任何平滑映射 - 隐藏层数>2:Additional layers can learn complex representations (sort ofautomatic feature engineering) for layer layers.
多出来的隐藏层可以学习复杂的描述
层数越深,理论上拟合函数的能力增强,效果按理说会更好,但是实际上更深的层数可能会带来过拟合的问题,同时也会增加训练难度,使模型难以收敛。因此我的经验是,在使用BP神经网络时,最好可以参照已有的表现优异的模型,如果实在没有,则根据上面的表格,从一两层开始尝试,尽量不要使用太多的层数。在CV、NLP等特殊领域,可以使用CNN、RNN、attention等特殊模型,不能不考虑实际而直接无脑堆砌多层神经网络。尝试迁移和微调已有的预训练模型,能取得事半功倍的效果。——Deep learning, 2016
4 连接权值
不需要自己设置值,连接权值是神经网络训练后得到的。如果使用MATLAB编程的话不需要自己设定,newff之后会自动赋值。
5 阈值
等待更新。
6 学习速率
合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。它指导我们在梯度下降法中,如何使用损失函数的梯度调整网络权重的超参数。
如果学习率过小,损失函数的变化速度会很慢,大大增加网络的收敛复杂度,并且很容易困在局部最小值;如果学习率过大,可能会使损失函数直接越过全局最优点,梯度在最小值附近来回震荡,甚至可能无法收敛。
目前共同认同的学习率设置标准为:首先设置一个较大的学习率,使网络的损失值快速下降,然后随着迭代次数的增加一点点减少,防止越过全局最优解。
7 激励函数
又叫做激活函数,常见的激活函数有阈值型、线性、非线性。BP神经网络的激活函数必须是处处可微的(一阶导数存在,从而可以严格利用梯度法进行推算,权值修正的解析式十分明确),所以它不能采用二值型的阈值函数或符号函数,常用的激活函数为S型对数函数、正切函数或线性函数。
因为S型函数具有非线性放大系数功能,它可以把输入从负无穷大到正无穷大的信号,变换成-1到1之间输出,对较大的输人信号,放大系数较小;而对较小的输人信号,放大系数则较大,所以采用S型激活函数可以去处理和逼近非线性的输入/输出关系。不过,如果在输出层采用S型函数,输出则被限制到一个很小的范围了,若采用线性激活函数,则可使网络输出任何值。所以只有当希望对网络的输出进行限制,如限制在0和1之间,那么在输出层应当包含S型激活函数。在一般情况下,均是在隐含层采用S型激活函数,而输出层采用线性激活函数。
四、数据归一化
概念:数据归一化方法是神经网络预测前对数据常做的一种处理方法。数据归一化处理把所有数据都转化为[0,1]之间的数。
目的:取消各维数据间数量级差别,避免因为输入输出数据数量级差别较大而造成神经网络预测误差较大。
方法:数据归一化的方法主要有以下两种。
①最大最小法
其中,xmin为数据序列中的最小值,xmax为最大值。
②平均数方差法
其中,xmean为平均值,xvar为方差。
参考文献:《MATLAB神经网络案例分析》《面向MATLAB工具箱的神经网络理论与应用》