二维Poisson方程五点差分格式及简单求解方法Python实现
二维Poisson方程简介
给出 二维 P o i s s o n Poisson Poisson 方程 D i r i c h l e t Dirichlet Dirichlet 边值问题:
{ − Δ u = f ( x , y ) ( x , y ) ∈ Ω u = φ ( x , y ) ( x , y ) ∈ Γ \begin{cases} - \Delta u = f(x, y) \quad (x, y) \in \Omega \\ u = \varphi(x, y) \quad (x, y) \in \Gamma \end{cases} {−Δu=f(x,y)(x,y)∈Ωu=φ(x,y)(x,y)∈Γ
为简单起见, 假设 Ω = [ a , b ] × [ c , d ] \Omega = [a, b] \times [c, d] Ω=[a,b]×[c,d]
五点差分格式建立
将区间 [ a , b ] [a, b] [a,b] 作 m m m 等分, 记 h 1 = ( b − a ) / m , x i = a + i h 1 , 0 ≤ i ≤ m i h_1 = (b - a ) / m, x_i = a + ih_1, 0 \leq i \leq m_i h1=(b−a)/m,xi=a+ih1,0≤i≤mi; 将区间 [ c , d ] [c, d] [c,d] 作 n 等分, 记 h 2 = ( d − c ) / n , y j = c + j h 2 , 0 ≤ j ≤ n h_2 = (d - c) / n, y_j = c + jh_2, 0 \leq j \leq n \ h2=(d−c)/n,yj=c+jh2,0≤j≤n 称 h 1 h_1 h1 为 x x x 方向的步长, h 2 h_2 h2为 y y y 方向上的步长, 用两簇平行线
x = x i , 0 ≤ i ≤ m x = x_i, \quad 0 \leq i \leq m x=xi,0≤i≤m y = y j , 0 ≤ j ≤ n y = y_j, \quad 0 \leq j \leq n y=yj,0≤j≤n
将区域 Ω \Omega Ω剖分为 m n mn mn个小矩形, 称两簇直线的交点 ( x i , y i ) (x_i ,y_i) (xi,yi) 为网格结点.
记
Ω h = { ( x i , y j ) ∣ 0 ≤ i ≤ m , 0 ≤ j ≤ n } \Omega_h = \left\lbrace (x_i, y_j)| 0 \leq i \leq m, \ 0 \leq j \leq n \right\rbrace Ωh={(xi,yj)∣0≤i≤m, 0≤j≤n}
称属于 Ω \Omega Ω的结点
Ω ˚ h = { ( x i , y j ) ∣ 1 ≤ i ≤ m − 1 , 1 ≤ j ≤ n − 1 } \mathring{\Omega}_h = \left\lbrace (x_i, y_j) | 1 \leq i \leq m-1, 1 \leq j \leq n-1 \right\rbrace Ω˚h={(xi,yj)∣1≤i≤m−1,1≤j≤n−1}
称为内结点, 称位于 Γ h = Ω h \Gamma_h = \Omega_h Γh=Ωh \ Ω ˚ h \mathring{\Omega}_h Ω˚h上的结点为边界结点
记
ω = { ( i , j ) ∣ ( x i , x j ) ∈ Ω ˚ h } , γ = { ( i , j ) ∣ ( x i , y j ) ∈ Γ h } \omega = \left\lbrace (i, j) | (x_i, x_j) \in \mathring{\Omega}_h \right\rbrace, \qquad \gamma = \left\lbrace (i,j) | (x_i, y_j) \in \Gamma_h \right\rbrace ω={(i,j)∣(xi,xj)∈Ω˚h},γ={(i,j)∣(xi,yj)∈Γh}
记
S h = { v ∣ v = { v i j ∣ 0 ≤ i ≤ m , 0 ≤ j ≤ n } 为 Ω h 上的网格函数 } S_h = \left\lbrace v | v = \left\lbrace v_{ij} | 0 \leq i \leq m, \ 0 \leq j \leq n\right\rbrace \text{为} \Omega_h \text{上的网格函数}\right\rbrace Sh={v∣v={vij∣0≤i≤m, 0≤j≤n}为Ωh上的网格函数}
设 v = { v i j ∣ 0 ≤ i ≤ m , 0 ≤ j ≤ n } ∈ S h v = \left\lbrace v_{ij\ } | 0 \leq i \leq m, 0 \leq j \leq n \right\rbrace \in S_h v={vij ∣0≤i≤m,0≤j≤n}∈Sh 给出如下记号:
D x v i j = 1 h 1 ( v i + 1 , j − v i j ) , D x ˉ v i j = 1 h 1 ( v i j − v i − 1 , j ) D_{x}v_{ij} = \dfrac{1}{h_1}(v_{i+1, j} - v_{ij} \ ), \qquad D_{\bar{x}}v_{ij} = \dfrac{1}{h_1}(v_{ij} - v_{i-1, j} \ ) Dxvij=h11(vi+1,j−vij ),Dxˉvij=h11(vij−vi−1,j ) D y v i j = 1 h 2 ( v i , j + 1 − v i j ) , D y ˉ v i j = 1 h 2 ( v i j − v i , j − 1 ) D_{y}v_{ij} = \dfrac{1}{h_2}(v_{i, j+1} - v_{ij} \ ), \qquad D_{\bar{y}}v_{ij} = \dfrac{1}{h_2}(v_{ij} - v_{i, j-1} \ ) Dyvij=h21(vi,j+1−vij ),Dyˉvij=h21(vij−vi,j−1 ) δ x 2 v i j = 1 h 1 ( D x v i j − D x ˉ v i j ) , δ y 2 v i j = 1 h 2 ( D y v i j − D y ˉ v i j ) \delta_{x}^2v_{ij} = \dfrac{1}{h_1}(D_{x}v_{ij} - D_{\bar{x}}v_{ij}), \qquad \delta_{y}^2v_{ij} = \dfrac{1}{h_2}(D_{y}v_{ij} - D_{\bar{y}}v_{ij}) δx2vij=h11(Dxvij−Dxˉvij),δy2vij=h21(Dyvij−Dyˉvij)
∥ v ∥ ∞ = max 0 ≤ i ≤ m 0 ≤ j ≤ n ∣ v i j ∣ \|v\|_{\infty} = \max\limits_{0 \leq i \leq m0 \\ \leq j \leq n} |v_{ij}| ∥v∥∞=0≤i≤m0≤j≤nmax∣vij∣ 称为 v v v 的无穷范数.
下面在结点处考虑上述椭圆型方程边值问题:
− [ ∂ 2 u ∂ x 2 ( x i , y j ) + ∂ 2 u ∂ y 2 ( x i , y j ) ] = f ( x i , y j ) , ( i , j ) ∈ ω - \left[\dfrac{\partial^2 u}{\partial x^2}(x_i, y_j) + \dfrac{\partial^2 u}{\partial y^2}(x_i, y_j)\right] = f(x_i, y_j), \qquad (i, j) \in \omega −[∂x2∂2u(xi,yj)+∂y2∂2u(xi,yj)]=f(xi,yj),(i,j)∈ω u ( x i , y j ) = φ ( x i , y j ) , ( i , j ) ∈ γ u(x_i, y_j) = \varphi(x_i, y_j), \qquad (i, j) \in \gamma u(xi,yj)=φ(xi,yj),(i,j)∈γ
定义 Ω h \Omega_h Ωh上的网格函数:
U = { U i j ∣ 0 ≤ i ≤ m , 0 ≤ j ≤ n } , U = \left\lbrace U_{ij}| 0 \leq i \leq m , \ 0 \leq j \leq n \right\rbrace, U={Uij∣0≤i≤m, 0≤j≤n},
其中
U i j = u ( x i , y j ) , 0 ≤ i ≤ m , 0 ≤ j ≤ n . U_{ij} = u(x_i, y_j), \qquad 0 \leq i \leq m , \quad 0 \leq j \leq n. Uij=u(xi,yj),0≤i≤m,0≤j≤n.
将原方程中的二阶导数项利用差分估计得:
∂ 2 u ∂ x 2 ( x i , y j ) = 1 h 1 2 [ u ( x i − 1 , y j ) − 2 u ( x i , y j ) + u ( x i + 1 , y j ) ] − h 1 2 12 ∂ 4 u ( ξ i j , y j ) ∂ x 4 \dfrac{\partial^2 u}{\partial x^2}(x_i, y_j) = \dfrac{1}{h_1^2}\left[ u(x_{i-1}, y_j)- 2u(x_i, y_j) + u(x_{i+1}, y_j)\right] - \dfrac{h_1^2}{12}\dfrac{\partial^4 u(\xi_{ij}, y_j)}{\partial x^4} ∂x2∂2u(xi,yj)=h121[u(xi−1,yj)−2u(xi,yj)+u(xi+1,yj)]−12h12∂x4∂4u(ξij,yj) = δ x 2 U i j − h 1 2 12 ∂ 4 u ( ξ i j , y j ) ∂ x 4 , x i − 1 < ξ i j < x i + 1 = \delta_x^2U_{ij} - \dfrac{h_1^2}{12} \dfrac{\partial^4 u(\xi_{ij}, y_j)}{\partial x^4}, \qquad x_{i-1} < \xi_{ij} < x_{i+1} =δx2Uij−12h12∂x4∂4u(ξij,yj),xi−1<ξij<xi+1
∂ 2 u ∂ y 2 ( x i , y j ) = 1 h 2 2 [ u ( x i , y j − 1 ) − 2 u ( x i , y j ) + u ( x i , y j + 1 ) ] − h 2 2 12 ∂ 4 u ( x i , η i j ) ∂ y 4 \dfrac{\partial^2 u}{\partial y^2}(x_i, y_j) = \dfrac{1}{h_2^2}\left[ u(x_i, y_{j - 1})- 2u(x_i, y_j) + u(x_i, y_{j+1})\right] - \dfrac{h_2^2}{12}\dfrac{\partial^4 u(x_i, \eta_{ij})}{\partial y^4} ∂y2∂2u(xi,yj)=h221[u(xi,yj−1)−2u(xi,yj)+u(xi,yj+1)]−12h22∂y4∂4u(xi,ηij)
= δ y 2 U i j − h 2 2 12 ∂ 4 u ( x i , η i j ) ∂ y 4 , y j − 1 < η i j < y j + 1 = \delta_y^2U_{ij} - \dfrac{h_2^2}{12}\dfrac{\partial^4 u(x_i, \eta_{ij})}{\partial y^4}, \qquad y_{j-1} < \eta_{ij} < y_{j + 1} =δy2Uij−12h22∂y4∂4u(xi,ηij),yj−1<ηij<yj+1
代入原方程中, 并略去高阶小量项 R i j = − h 1 2 12 ∂ 4 u ( ξ i j , y j ) ∂ x 4 − h 2 2 12 ∂ 4 u ( x i , η i j ) ∂ y 4 R_{ij} = -\dfrac{h_1^2}{12}\dfrac{\partial^4 u(\xi_{ij}, y_j)}{\partial x^4} - \dfrac{h_2^2}{12}\dfrac{\partial^4u(x_i, \eta_{ij})}{\partial y^4} Rij=−12h12∂x4∂4u(ξij,yj)−12h22∂y4∂4u(xi,ηij) 之后利用 u i j u_{ij} uij 代替 U i j U_{ij} Uij得到如下差分格式:
− ( δ x 2 u i j + δ y 2 u i j ) = f ( x i , y j ) , ( i , j ) ∈ ω -(\delta_x^2u_{ij} + \delta_y^2u_{ij}) = f(x_i, y_j),\quad (i, j) \in \omega −(δx2uij+δy2uij)=f(xi,yj),(i,j)∈ω u i j = φ ( x i , y j ) , ( i , j ) ∈ γ u_{ij} = \varphi(x_i, y_j) ,\quad (i, j) \in \gamma uij=φ(xi,yj),(i,j)∈γ
差分格式的求解
改写原方程为矩阵方程
差分格式是以 { u i j ∣ 1 ≤ i ≤ m − 1 , 1 ≤ j ≤ n − 1 } \left\lbrace u_{ij} | 1 \leq i \leq m-1, 1 \leq j \leq n-1 \right\rbrace {uij∣1≤i≤m−1,1≤j≤n−1} 为未知量的线性方程组
改写 − ( δ x 2 u i j + δ y 2 u i j ) = f ( x i , y j ) -(\delta_x^2u_{ij} + \delta_y^2u_{ij}) = f(x_i, y_j) −(δx2uij+δy2uij)=f(xi,yj)为:
− 1 h 2 2 u i , j − 1 − 1 h 1 2 u i − 1 , j + 2 ( 1 h 1 2 + 1 h 2 2 ) u i j − 1 h 1 2 u i + 1 , j − 1 h 2 2 u i , j + 1 = f ( x i , y j ) -\frac{1}{h_2^2}u_{i, \ j-1}-\frac{1}{h_1^2}u_{i-1, \ j} + 2(\frac{1}{h_1^2} + \frac{1}{h_2^2})u_{ij}-\frac{1}{h_1^2}u_{i+1, \ j} -\frac{1}{h_2^2}u_{i, \ j+1}= f(x_i, y_j) −h221ui, j−1−h121ui−1, j+2(h121+h221)uij−h121ui+1, j−h221ui, j+1=f(xi,yj) 1 ≤ i ≤ m − 1 , 1 ≤ j ≤ n − 1 1 \leq i \leq m-1, \quad 1 \leq j \leq n-1 1≤i≤m−1,1≤j≤n−1
记:
u j = ( u 1 j u 2 j ⋮ u m − 1 , j ) , 0 ≤ j ≤ n \pmb{u}_j = \begin{pmatrix} u_{1j} \\ u_{2j} \\ \vdots \\ u_{m-1, j} \end{pmatrix}, \quad 0 \leq j \leq n uuuj=⎝⎜⎜⎜⎛u1ju2j⋮um−1,j⎠⎟⎟⎟⎞,0≤j≤n
改写方程为:
D u j − 1 + C u j + D u j + 1 = f j , 1 ≤ j ≤ n − 1 \pmb{Du}_{j-1} + \pmb{Cu}_{j} + \pmb{Du}_{j+1} = \pmb{f}_j, \quad 1\leq j \leq n-1 DuDuDuj−1+CuCuCuj+DuDuDuj+1=fffj,1≤j≤n−1
C = ( 2 ( 1 h 1 2 + 1 h 2 2 ) − 1 h 1 2 − 1 h 1 2 2 ( 1 h 1 2 + 1 h 2 2 ) − 1 h 1 2 ⋱ ⋱ ⋱ − 1 h 1 2 2 ( 1 h 1 2 + 1 h 2 2 ) − 1 h 1 2 − 1 h 1 2 2 ( 1 h 1 2 + 1 h 2 2 ) ) \pmb{C} = \begin{pmatrix} 2 \left( \dfrac{1}{h_1^2} + \dfrac{1}{h_2^2}\right) & -\dfrac{1}{h_1^2} & & & & \\ -\dfrac{1}{h_1^2}& 2 \left( \dfrac{1}{h_1^2} + \dfrac{1}{h_2^2}\right) & -\dfrac{1}{h_1^2}& & & \\ & \ddots & \ddots & \ddots & & \\ & & -\dfrac{1}{h_1^2} & 2 \left( \dfrac{1}{h_1^2} + \dfrac{1}{h_2^2}\right) & -\dfrac{1}{h_1^2} \\ & & & -\dfrac{1}{h_1^2} & 2 \left( \dfrac{1}{h_1^2} + \dfrac{1}{h_2^2}\right) \end{pmatrix} CCC=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛2(h121+h221)−h121−h1212(h121+h221)⋱−h121⋱−h121⋱2(h121+h221)−h121−h1212(h121+h221)⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞
D = ( − 1 h 2 2 − 1 h 2 2 ⋱ − 1 h 2 2 − 1 h 2 2 ) f j = ( f ( x 1 , y j ) + 1 h 1 2 φ ( x 0 , y j ) f ( x 2 , y j ) ⋮ f ( x m − 2 , y j ) f ( x m − 1 , y j ) + 1 h 1 2 φ ( x m , y j ) ) \pmb{D} = \begin{pmatrix} -\dfrac{1}{h_2^2} & & & & \\ & -\dfrac{1}{h_2^2} & & & \\ & & \ddots & & \\ & & & -\dfrac{1}{h_2^2} & \\ & & & & -\dfrac{1}{h_2^2}\end{pmatrix} \qquad \pmb{ f }_j = \begin{pmatrix} f(x_1, y_j) + \dfrac{1}{h_1^2} \varphi(x_0, y_j) \\ f(x_2, y_j) \\ \vdots \\ f(x_{m-2}, y_j) \\ f(x_{m-1}, y_j) + \dfrac{1}{h_1^2} \varphi(x_m, y_j)\end{pmatrix} DDD=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛−h221−h221⋱−h221−h221⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞fffj=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛f(x1,yj)+h121φ(x0,yj)f(x2,yj)⋮f(xm−2,yj)f(xm−1,yj)+h121φ(xm,yj)⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞
进一步改写, 得到:
( C D D C D ⋱ ⋱ ⋱ D C D D C ) ( u 1 u 2 ⋮ u n − 2 u n − 1 ) = ( f 1 − D u 0 f 2 ⋮ f n − 2 f n − 1 − D u n ) \begin{pmatrix} \pmb{C} & \pmb{D} & & & \\ \pmb{D} & \pmb{C} & \pmb{D} & & \\ & \ddots & \ddots & \ddots & \\ & & \pmb{D} & \pmb{C} & \pmb{D} \\ & & & \pmb{D} & \pmb{C} \end{pmatrix} \begin{pmatrix} \pmb{u}_1 \\ \pmb{u}_2 \\ \vdots \\ \pmb{u}_{n-2} \\ \pmb{u}_{n-1}\end{pmatrix} = \begin{pmatrix} \pmb{f}_1 - \pmb{Du}_0 \\ \pmb{f}_2 \\ \vdots \\ \pmb{f}_{n-2} \\ \pmb{f}_{n-1} - \pmb{Du}_n\end{pmatrix} ⎝⎜⎜⎜⎜⎛CCCDDDDDDCCC⋱DDD⋱DDD⋱CCCDDDDDDCCC⎠⎟⎟⎟⎟⎞⎝⎜⎜⎜⎜⎜⎛uuu1uuu2⋮uuun−2uuun−1⎠⎟⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎜⎜⎛fff1−DuDuDu0fff2⋮fffn−2fffn−1−DuDuDun⎠⎟⎟⎟⎟⎟⎞
五点差分方法的简单实现
显然, 一个比较简单的方法就是直接求解上述线性方程组.在本文中直接使用求解线性方程组的方法进行暴力求解,对于矩阵规模比较大的时候,一般会使用迭代算法或是其他快速算法对上述线性方程组进行求解,在后面的文章中如果有时间会陆续进行介绍。
稀疏矩阵
上述线性方程组的矩阵为稀疏矩阵, 需要引入相关的稀疏矩阵操作,节省内存.
P y t h o n Python Python 中 稀疏矩阵结构体 在 scipy.sparse 模块下.
P y t h o n Python Python 中 用于求解大型稀疏矩阵方程组的函数为 scipy.sparse.linalg 模块下的 spsolve() 函数.
分别介绍这两部分
Python中的稀疏矩阵数据结构
由于 使用 spsolve() 函数时,传入的矩阵希望是 C S R CSR CSR 或 C S C CSC CSC格式的系数矩阵, 因此仅介绍两种格式的稀疏矩阵.
以下面矩阵为例,分别介绍其 C S R CSR CSR格式存储以及 C S C CSC CSC格式存储.
A = ( 0 0 0 10 21 0 33 0 0 0 3 0 12 1 0 4 ) A = \begin{pmatrix} 0 & 0 & 0 & 10 \\ 21 & 0 & 33 & 0 \\ 0 & 0 & 3 & 0 \\ 12 & 1 & 0 & 4 \end{pmatrix} A=⎝⎜⎜⎛02101200010333010004⎠⎟⎟⎞
C S R ( 压 缩 行 稀 疏 行 ) : \color{red}{CSR (压缩行稀疏行):} CSR(压缩行稀疏行):
调用格式:
csr_matrix((data, indices, indptr), shape=(a, b), dtype = float)
csr_matrix 详解:
$ CSR $格式的稀疏矩阵对上述矩阵分别利用三个数组 data, indices, indptr 如下:
data = [10, 21, 33, 3, 12, 1, 4]
indices = [3, 0, 2, 2, 0, 1 , 3]
indptr = [0, 1, 3, 4, 7]
其中:
data (数据): 表示存储的非零有数值 .
indices (列索引): 按照顺序存储非零有效数值的列标号.
indptr (行偏移量): 表示indices中行元素的起始位置和终止位置, 如果indptr[i] == indptr[i+1]则表示改行元素全为0, 如果初始矩阵有 m 行, 则 len(indptr) == m+1.
示范
from scipy.sparse import csr_matrix, csc_matrix
data = [10, 21, 33, 3, 12, 1, 4]
indices = [3, 0, 2, 2, 0, 1, 3]
indptr = [0, 1, 3, 4, 7]
A = csr_matrix((data, indices, indptr), shape = (4,4))
print(A)
稀疏矩阵中提供 toarray()方法将一个稀疏矩阵转换为一个普通矩阵.
示范
print(A.toarray())
即可将A转换为对应的numpy矩阵.
或者可以直接通过将满矩阵 B 传入 csr_matrix 函数来获取稀疏矩阵
通过调用稀疏矩阵对象的 data, indices,indptr 属性, 查看相应的数据
示范
print('data = ', C.data)
print('indices = ', C.indices)
print('indptr = ', C.indptr)
输出结果:
data = [10 21 33 3 12 1 4]
indices = [3 0 2 2 0 1 3]
indptr = [0 1 3 4 7]
C S C ( 压 缩 列 稀 疏 行 ) : \color{red}{CSC (压缩列稀疏行):} CSC(压缩列稀疏行):
调用格式:
csc_matrix((data, indices, indptr), shape=(a, b), dtype=float)
C S C CSC CSC稀疏矩阵的存储方式与 C S R CSR CSR格式稀疏矩阵的存储方式大致相同,将 C S R CSR CSR格式中的行(列) 换为列(行)即可.
Python 中用于快速创建稀疏矩阵的函数
scipy.sparse 模块下提供了以下函数用于快速创建稀疏矩阵, 调用格式如下:
sparse.eye(20, 20, format = 'csr') # 创建稀疏格式的单位矩阵
sparse.spdiags(array, n, row, col,format = 'csr') # 创建对角矩阵,其中n表示在主对角线上方n个单位的对角线上创建
其余更多的函数见scipy的官方文档.
Python 中用于求解稀疏矩阵方程组的函数
对于稀疏矩阵方程组的求解,需要调用 scipy.sparse.linalg模块下的spsolve()函数, 函数使用格式如下:
spsolve(spA, b)
其中 spA 是 C S R CSR CSR 或者 C S C CSC CSC 格式存储的稀疏矩阵 .
s p s o l v e ( ) 使 用 示 例 : \color{red}{spsolve() 使用示例:} spsolve()使用示例:
求解线性方程组:
( 0 0 0 10 21 0 33 0 0 0 3 0 12 1 0 4 ) X = ( 1 2 3 4 ) \begin{pmatrix} 0 & 0 & 0 & 10 \\ 21 & 0 & 33 & 0 \\ 0 & 0 & 3 & 0 \\ 12 & 1 & 0 & 4 \end{pmatrix} X = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4\end{pmatrix} ⎝⎜⎜⎛02101200010333010004⎠⎟⎟⎞X=⎝⎜⎜⎛1234⎠⎟⎟⎞
其中,左端项矩阵要求用csr_matrix或者csc_matrix进行创建.
from scipy.sparse.linalg import spsolve
data = [10, 21, 33, 3, 12, 1, 4]
indices = [3, 0, 2, 2, 0, 1, 3]
indptr = [0, 1, 3, 4, 7]
spA = csr_matrix((data, indices, indptr), shape = (4, 4))
print(spA.toarray())
b = np.arange(1, 5)
spsolve(spA, b)
结果如下:
array([-1.47619048, 21.31428571, 1. , 0.1 ])
矩阵的 Kronecker 乘积
为了快速组装左端项矩阵,可以利用 k r o n e c k e r kronecker kronecker积.
假设给定一个大小为 m 1 × m 2 m_1 \times m_2 m1×m2 的矩阵 A A A 和一个大小为 n 1 × n 2 n_1 \times n_2 n1×n2的矩阵, 定义 A A A 和 B B B 之间的 K r o n e c k e r Kronecker Kronecker 乘积 A ⊗ B A \otimes B A⊗B 如下:
A ⊗ B = ( a 11 B a 12 B ⋯ a 1 m 2 B a 21 B a 22 B ⋯ a 2 m 2 B ⋮ ⋮ ⋱ ⋮ a m 1 1 B a m 1 2 B ⋯ a m 1 m 2 B ) A \otimes B = \begin{pmatrix} a_{ 11 } B & a_{ 12 }B & \cdots & a_{1m_2}B \\ a_{ 21 } B & a_{ 22 }B & \cdots & a_{2m_2}B \\ \vdots & \vdots & \ddots & \vdots \\ a_{ m_1 1 } B & a_{ m_1 2 }B & \cdots & a_{m_1 m_2}B \\ \end{pmatrix} A⊗B=⎝⎜⎜⎜⎛a11Ba21B⋮am11Ba12Ba22B⋮am12B⋯⋯⋱⋯a1m2Ba2m2B⋮am1m2B⎠⎟⎟⎟⎞
例如 : 给定向量 u ⃗ = ( 1 2 ) \vec{ u } = \begin{pmatrix} 1 \\ 2 \end{pmatrix} u=(12), v ⃗ = ( 3 4 ) \vec{ v } = \begin{pmatrix} 3 \\ 4 \end{pmatrix} v=(34) 容易计算:
u ⃗ ⊗ v ⃗ = ( 3 4 6 8 ) \vec{ u } \otimes \vec{ v } = \begin{pmatrix} 3 \\ 4 \\ 6 \\ 8 \end{pmatrix} u⊗v=⎝⎜⎜⎛3468⎠⎟⎟⎞
有关 K r o n e c k e r Kronecker Kronecker乘积的更多描述可以查看相关数学资料.
N u m p y Numpy Numpy 下的 K r o n e c k e r Kronecker Kronecker积
n u m p y numpy numpy 模块下的 kron函数专门用于计算 两个矩阵的 k r o n e c k e r kronecker kronecker乘积
示范:
import numpy as np
A = np.array([ [1], [2] ], dtype = np.float64)
B = np.array([ [3], [4] ], dtype = np.float64)
np.kron(A, B)
输出结果:
[[3.]
[4.]
[6.]
[8.]]
A2 = np.array([ [1, 2], [3, 1] ])
B2 = np.array([ [0, 3], [2, 1] ])
np.kron(A2, B2)
输出结果
array([[0, 3, 0, 6],
[2, 1, 4, 2],
[0, 9, 0, 3],
[6, 3, 2, 1]])
稀疏格式下的 kron 函数
scipy.sparse模块下提供了稀疏格式的 kron 函数, 返回两个稀疏格式矩阵的 kronecker 乘积.
示范:
from scipy import sparse
A2 = sparse.csr_matrix(A2)
B2 = sparse.csr_matrix(B2)
sparse.kron(A2, B2).toarray()
输出结果:
array([[0, 3, 0, 6],
[2, 1, 4, 2],
[0, 9, 0, 3],
[6, 3, 2, 1]], dtype=int32)
五点差分格式数值实验
编写程序实现五点差分格式,并利用下面的问题进行数值模拟:
− ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) = ( π 2 − 1 ) e x s i n ( π y ) , 0 < x < 2 , 0 < y < 1 -\left( \dfrac{\partial^2u}{\partial x^2} + \dfrac{\partial^2u}{\partial y^2} \right) = (\pi^2 - 1)e^xsin(\pi y), \quad 0 < x < 2, \quad 0 < y < 1 −(∂x2∂2u+∂y2∂2u)=(π2−1)exsin(πy),0<x<2,0<y<1 u ( 0 , y ) = s i n ( π y ) , u ( 2 , y ) = e 2 s i n ( π y ) , 0 ≤ y ≤ u(0, y) = sin(\pi y), \quad u(2, y) = e^2sin(\pi y), \quad 0 \leq y \leq u(0,y)=sin(πy),u(2,y)=e2sin(πy),0≤y≤ u ( x , 0 ) = 0 , u ( x , 1 ) = 0 , 0 ≤ x ≤ 2 u(x, 0) = 0, \quad u(x, 1) = 0, \quad 0 \leq x \leq 2 u(x,0)=0,u(x,1)=0,0≤x≤2
要求如下:
- 分别在如下网格上对问题进行求解:
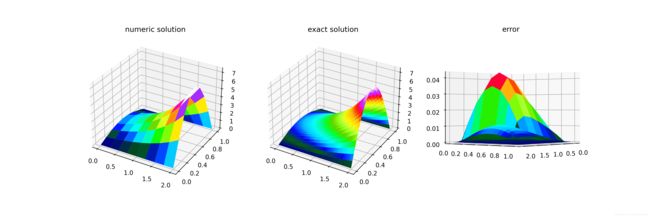
( h 1 , h 2 ) / ( x , y ) = ( 1 8 , 1 8 ) ; ( 1 16 , 1 16 ) ; ( 1 32 , 1 32 ) ; ( 1 64 , 1 64 ) (h_1, h_2) / (x, y) = (\dfrac{1}{8}, \dfrac{1}{8}); (\dfrac{1}{16}, \dfrac{1}{16});(\dfrac{1}{32}, \dfrac{1}{32});(\dfrac{1}{64}, \dfrac{1}{64}) (h1,h2)/(x,y)=(81,81);(161,161);(321,321);(641,641) - 绘制 ( h 1 , h 2 ) / ( x , y ) = ( 1 8 , 1 8 ) (h_1, h_2) / (x, y) = (\dfrac{1}{8}, \dfrac{1}{8}) (h1,h2)/(x,y)=(81,81)网格上的数值解曲面以及真解曲面
- 绘制各个网格上数值解的误差曲面
- 计算上述各个数值解与真解之间的全局最大模误差, 并验证上述数值格式所得到的数值解最大模误差阶为 O ( h 1 2 + h 2 2 ) O(h_1^2 + h_2^2) O(h12+h22)
已知上述方程的真解为: u ( x , y ) = e x s i n ( π y ) u(x, y) = e^x sin(\pi y) u(x,y)=exsin(πy)
导入需要模块
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy import sparse as ss
from scipy.sparse.linalg import spsolve
模型参数
class PdeModel:
def __init__(self, x, y):
self.x = x
self.y = y
def space_grid(self, Nx, Ny):
X = np.linspace(self.x[0], self.x[1], Nx + 1)
Y = np.linspace(self.y[0], self.y[1], Ny + 1)
h1 = (self.x[1] - self.x[0]) / Nx
h2 = (self.y[1] - self.y[0]) / Ny
return h1, h2, X, Y
def source(self, X, Y):
return (np.pi ** 2 - 1) * np.exp(X) * np.sin(np.pi * Y)
def solution(self, X, Y):
YY, XX = np.meshgrid(Y, X)
return np.exp(XX) * np.sin(np.pi * YY)
def left_solution(self, Y):
return np.sin(np.pi * Y)
def right_solution(self, Y):
return np.exp(2) * np.sin(np.pi * Y)
def upper_solution(self, X):
return np.zeros(len(X))
def bottom_solution(self, X):
return np.zeros(len(X))
误差函数
def fd2d_epbvp_error(solution, uh, XY):
ee = np.abs((solution(XY) - uh))
emax = np.max(ee)
return emax, ee
差分格式简单实现
def fd2d_epbvp(pde, NS):
Nx = NS[0]
Ny = NS[1]
h1, h2, X, Y = pde.space_grid(Nx, Ny)
YY, XX = np.meshgrid(Y, X)
uh = np.zeros((Nx + 1, Ny + 1))
uh[0, :] = pde.left_solution(Y)
uh[-1, :] = pde.right_solution(Y)
uh[:, 0] = pde.bottom_solution(X)
uh[:, -1] = pde.upper_solution(X)
tmp = np.ones(Nx - 1)
D = ss.diags([2 * tmp, -tmp, -tmp], [0, -1, 1], format = 'csc', dtype = np.float64)
C = np.diag(-tmp / h2 ** 2)
Id = ss.eye(Ny - 1, format = 'csc')
DD = ss.kron(Id, D, format = 'csc') / h1 ** 2 + ss.kron(D, Id, format = 'csc') / h2 ** 2
rhs = pde.source(XX[1: -1, 1: -1], YY[1: -1, 1: -1])
rhs[0, :] = rhs[0, :] + uh[0, 1:-1] / h1 ** 2
rhs[-1, :] = rhs[-1, :] + uh[-1, 1:-1] / h1 ** 2
rhs = rhs.T.flatten()
rhs[0: Nx - 1] = rhs[0: Nx - 1] - np.dot(C, uh[1:-1, 0])
rhs[1 - Nx:] = rhs[1 - Nx:] - np.dot(C, uh[1:-1, -1])
uh[1:-1, 1:-1] = spsolve(DD, rhs).reshape(Ny - 1, Nx - 1).T
return X, Y, uh
测试程序
def fd2d_epbvp_test():
# 初始化
x = np.array([0, 2])
y = np.array([0, 1])
NS = [np.array([8, 8]), np.array([16, 16]), np.array([32, 32]), np.array([64, 64])]
X_rec = []
Y_rec = []
XX_rec = []
YY_rec = []
uh_rec = []
ee_rec = []
emax_rec = np.zeros(4)
for i in range(4):
pde = PdeModel(x, y)
X, Y, uh = fd2d_epbvp(pde, NS[i])
YY, XX = np.meshgrid(Y, X)
X_rec.append(X)
Y_rec.append(Y)
XX_rec.append(XX)
YY_rec.append(YY)
uh_rec.append(uh)
emax, ee = fd2d_epbvp_error(pde.solution, uh, X, Y)
ee_rec.append(ee)
emax_rec[i] = emax
# 在最后一个网格上绘制真解图像, 以及第一个网格上的数值解图像
plt.figure(figsize=(15, 5))
ax1 = plt.subplot(131, projection='3d')
ax2 = plt.subplot(132, projection='3d')
ax3 = plt.subplot(133, projection='3d')
ax1.set_title('numeric solution')
ax2.set_title('exact solution')
ax3.set_title('error')
ax3.view_init(elev=0, azim=40)
ax1.plot_surface(XX_rec[0], YY_rec[0], uh_rec[0], cmap='gist_ncar')
ax2.plot_surface(XX_rec[-1], YY_rec[-1], pde.solution(X_rec[-1], Y_rec[-1]), cmap='gist_ncar')
for i in range(4):
ax3.plot_surface(XX_rec[i], YY_rec[i], ee_rec[i], cmap = 'gist_ncar', vmin = 0, vmax = 0.05)
plt.show()
print('E(2h, 2h) / E(h, h)')
for i in range(3):
print(emax_rec[i] / emax_rec[i + 1])
if __name__ == '__main__':
fd2d_epbvp_test()
求解结果:
| (h1, h2) \ (x, y) | Emax | E(2h, 2h) / E(h, h) |
|---|---|---|
| (1/ 8, 1 / 8) | 0.04303452888674553 | * |
| (1/ 16, 1 / 16) | 0.010886400216718606 | 3.9530540885917436 |
| (1/ 32, 1 / 32) | 0.0027306516871483666 | 3.9867406992824224 |
| (1/ 64, 1 / 64) | 0.0006841690298706737 | 3.9911945263943513 |
参考资料
[1]孙志忠.偏微分方程数值解法[M].北京:科学出版社,2015:34-42.