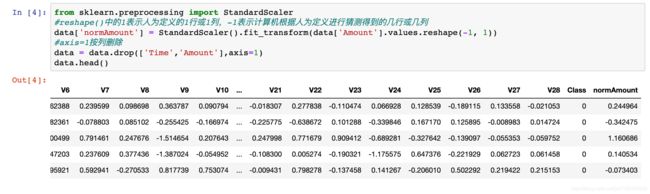
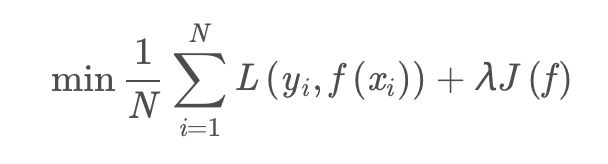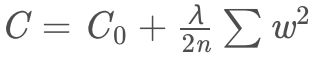NO.62——100天机器学习实践第五天:用逻辑回归模型分析信用卡欺诈案例
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline#分类计数
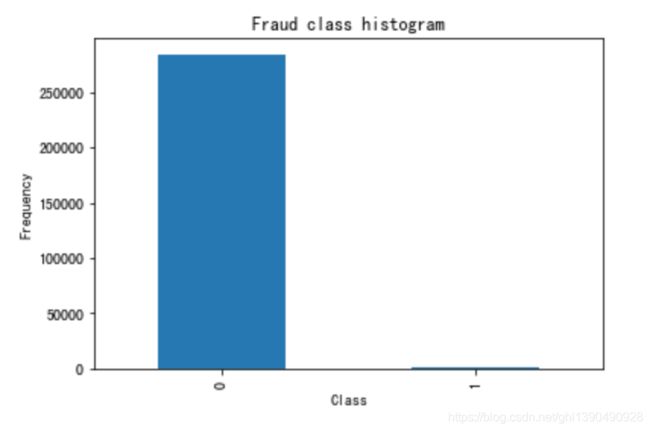
count_classes = pd.value_counts(data['Class'], sort = True).sort_index()
count_classes.plot(kind = 'bar')
plt.title("Fraud class histogram")
plt.xlabel("Class")
plt.ylabel("Frequency")解决样本不均衡:两种方法可以采用——过采样和下采样。过采样是对少的样本(此例中是类别为 1 的样本)再多生成些,使 类别为 1 的样本和 0 的样本一样多。而下采样是指,随机选取类别为 0 的样本,是类别为 0 的样本和类别为 1 的样本一样少。下采样的代码如下:
#训练集 loc根据index索引 iloc根据行号索引
X = data.loc[:, data.columns != 'Class']
#特征集
y = data.loc[:, data.columns == 'Class']
# Number of data points in the minority class
number_records_fraud = len(data[data.Class == 1]) #诈骗记录的条数
fraud_indices = np.array(data[data.Class == 1].index) #诈骗记录的下标
# Picking the indices of the normal classes
normal_indices = np.array(data[data.Class == 0].index) #正常记录的下标
#下采样 在normal_indices中随机选择number_records_fraud个,replace = False表示没有重复值
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
# 合并 the 2 indices
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
# Under sample dataset
under_sample_data = data.loc[under_sample_indices,:]
X_undersample = under_sample_data.loc[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.loc[:, under_sample_data.columns == 'Class']
# Showing ratio
print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("Total number of transactions in resampled data: ", len(under_sample_data))Percentage of normal transactions: 0.5 Percentage of fraud transactions: 0.5 Total number of transactions in resampled data: 984
from sklearn.model_selection import train_test_split
# Whole dataset 测试集占比0.3
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.3, random_state = 0)
print("Number transactions train dataset: ", len(X_train))
print("Number transactions test dataset: ", len(X_test))
print("Total number of transactions: ", len(X_train)+len(X_test))
# Undersampled dataset 。之所以划分两种数据集是因为通过下采样样本数较少
X_train_undersample, X_test_undersample, y_train_undersample, y_test_undersample = train_test_split(X_undersample
,y_undersample
,test_size = 0.3
,random_state = 0)
print("")
print("Number transactions train dataset: ", len(X_train_undersample))
print("Number transactions test dataset: ", len(X_test_undersample))
print("Total number of transactions: ", len(X_train_undersample)+len(X_test_undersample))Number transactions train dataset: 199364 Number transactions test dataset: 85443 Total number of transactions: 284807 Number transactions train dataset: 688 Number transactions test dataset: 296 Total number of transactions: 984
这里引入召回率和准确率的概念。
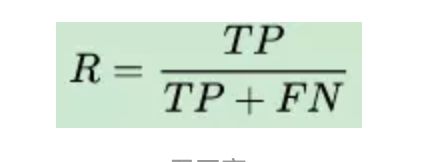
召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。这里会产生两种情况,一种是预测正确,把原来的正类预测成正类(TP),另一种就是预测错误,把原来的正类预测为负类(FN)。
准确率是针对预测正确的案例,不管是正类预测成正类,还是把负类预测出负类,比上所有样本。
(TP+TN)/(TP+FN+FP+TN)
TP,即 True Positive ,判断成了正例,判断正确;把正例判断为正例了
TN,即 True negative, 判断成了负例,判断正确,这叫去伪;把负例判断为负例了
FP,即False Positive ,判断成了正例,但是判断错了,也就是把负例判断为正例了
FN ,即False negative ,判断成了负例,但是判断错了,也就是把正例判断为负例了。
这里引入正则惩罚项。
模型选择的典型方法就是正则化。正则化是结构风险最小化策略的实现,是在经验风险吗上加上一个正则化项或惩罚项。正则化项一般是模型负责度的单调递增函数,模型越复杂,正则化值就越大。比如正则化相可以是模型参数向量的范数。
其中,第一项是经验风险,第二项为正则化项,lambda ≥ 0为调整两者之间关系的系数。正则化项可以取不同的形式。例如,回归问题中,损失函数是平方损失正则化项可以是参数向量的L2范数。正则化项也可以是参数辆的L1范数。
第一项的经验风险较小的模型可能较为复杂(有多个非零参数),这时第二项的模型复杂度会较大。正则化的作用是选择经验风险与模型复杂度同时较小的模型。正则化符合奥卡姆剃刀原理。奥卡姆剃刀原理应用于模型选择时变为以下想法:在所有可能选择的模型中,能够很好地解释数据并且十分简单的才是最好的模型,也就是应该选择的模型。从贝叶斯估计的角度来看,正则化对应于模型的先验概率,可以假设复杂的模型有较小的先验概率,简单的模型有较大的先验概率。
举一个简单的例子:
以最简单的线性分类为例,假设样本特征为X=[1,1,1,1],模型1的权重W1=[1,0,0,0],模型二权重W2=[0.25,0.25,0.25,0.25],虽然W1X=W2X=1;但是权重W1只关注一个特征(像素点),其余特征点都无效,模型具体、复杂、明显,能识别“正方形棉布材质的彩色手帕”,在训练集上训练完后容易导致过拟合,因为测试数据只要在这个像素点发生些许变化,分类结果就相差很大,而模型2的权重W2关注所有特征(像素点),模型更加简洁均匀、抽象,能识别“方形”,泛化能力强。通过L2正则化惩罚之后,模型1的损失函数会增加λ/8,模型2的损失函数会增加λ/32,显然,模型2更趋向让损失函数值更小。
#Recall = TP/(TP+FN) TP为推测正确且将正集推测为正,FN为推测错误且将正集推测为负
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import confusion_matrix,recall_score,classification_report def printing_Kfold_scores(x_train_data,y_train_data):
fold = KFold(5,shuffle=False)
# Different C parameters。逻辑回归的惩罚参数
c_param_range = [0.01,0.1,1,10,100]
results_table = pd.DataFrame(index = range(len(c_param_range)), columns = ['C_parameter','Mean recall score'])
results_table['C_parameter'] = c_param_range
# the k-fold will give 2 lists: train_indices = indices[0], test_indices = indices[1]
j = 0
for c_param in c_param_range:
print('-------------------------------------------')
print('C parameter: ', c_param)
print('-------------------------------------------')
print('')
recall_accs = []
#enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
for iteration, indices in enumerate(fold.split(x_train_data)):
#把c_param_range代入到逻辑回归模型中,并使用了l1正则化,小数据集可以使用liblinear'
lr = LogisticRegression(C = c_param,penalty = 'l1',solver='liblinear')
#使用indices[0]的数据进行拟合曲线,使用indices[1]的数据进
#values.ravel()用于将数组降到一维
lr.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
# Predict values using the test indices in the training data
y_pred_undersample = lr.predict(x_train_data.iloc[indices[1],:].values)
# Calculate the recall score and append it to a list for recall scores representing the current c_parameter
recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
recall_accs.append(recall_acc)
print('Iteration ', iteration,': recall score = ', recall_acc)
# The mean value of those recall scores is the metric we want to save and get hold of.
results_table.loc[j,'Mean recall score'] = np.mean(recall_accs)
j += 1
print('')
print('Mean recall score ', np.mean(recall_accs))
print('')
best_c = results_table.loc[results_table['Mean recall score'].astype(float).idxmax()]['C_parameter']
# Finally, we can check which C parameter is the best amongst the chosen.
print('*********************************************************************************')
print('Best model to choose from cross validation is with C parameter = ', best_c)
print('*********************************************************************************')
return best_cbest_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)------------------------------------------- C parameter: 0.01 ------------------------------------------- Iteration 0 : recall score = 0.8767123287671232 Iteration 1 : recall score = 0.9041095890410958 Iteration 2 : recall score = 0.9830508474576272 Iteration 3 : recall score = 0.9594594594594594 Iteration 4 : recall score = 0.9393939393939394 Mean recall score 0.932545232823849 ------------------------------------------- C parameter: 0.1 ------------------------------------------- Iteration 0 : recall score = 0.863013698630137 Iteration 1 : recall score = 0.8767123287671232 Iteration 2 : recall score = 0.9830508474576272 Iteration 3 : recall score = 0.9459459459459459 Iteration 4 : recall score = 0.8939393939393939 Mean recall score 0.9125324429480454 ------------------------------------------- C parameter: 1 ------------------------------------------- Iteration 0 : recall score = 0.863013698630137 Iteration 1 : recall score = 0.8904109589041096 Iteration 2 : recall score = 0.9830508474576272 Iteration 3 : recall score = 0.9594594594594594 Iteration 4 : recall score = 0.9090909090909091 Mean recall score 0.9210051747084484 ------------------------------------------- C parameter: 10 ------------------------------------------- Iteration 0 : recall score = 0.863013698630137 Iteration 1 : recall score = 0.8767123287671232 Iteration 2 : recall score = 0.9830508474576272 Iteration 3 : recall score = 0.9459459459459459 Iteration 4 : recall score = 0.9090909090909091 Mean recall score 0.9155627459783485 ------------------------------------------- C parameter: 100 ------------------------------------------- Iteration 0 : recall score = 0.8904109589041096 Iteration 1 : recall score = 0.863013698630137 Iteration 2 : recall score = 0.9830508474576272 Iteration 3 : recall score = 0.9594594594594594 Iteration 4 : recall score = 0.8939393939393939 Mean recall score 0.9179748716781454 ********************************************************************************* Best model to choose from cross validation is with C parameter = 0.01 *********************************************************************************
def plot_confusion_matrix(cm, classes,title='Confusion matrix',cmap=plt.cm.Blues):
'''这个方法用来输出和画出混淆矩阵的
'''
#cm为数据,interpolation='nearest'使用最近邻插值,cmap颜色图谱(colormap), 默认绘制为RGB(A)颜色空间
plt.imshow(cm,interpolation='nearest',cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
#xticks(刻度下标,刻度标签)
plt.xticks(tick_marks, classes, rotation=0)
plt.yticks(tick_marks, classes)
#text()命令可以在任意的位置添加文字
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
#自动紧凑布局
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
①使用下采样数据训练与测试
import itertools
lr = LogisticRegression(C = best_c, penalty = 'l1', solver='liblinear')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample = lr.predict(X_test_undersample.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()
②分割不同阈值,使用下采样数据进行训练
lr = LogisticRegression(C = best_c, penalty = 'l1', solver='liblinear')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
#获得预测样本的概率值
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)
#分割阈值
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
plt.figure(figsize=(10,10))
j = 1
for i in thresholds:
y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i
plt.subplot(3,3,j)
j += 1
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1] #0和1的分类
plot_confusion_matrix(cnf_matrix
, classes=class_names
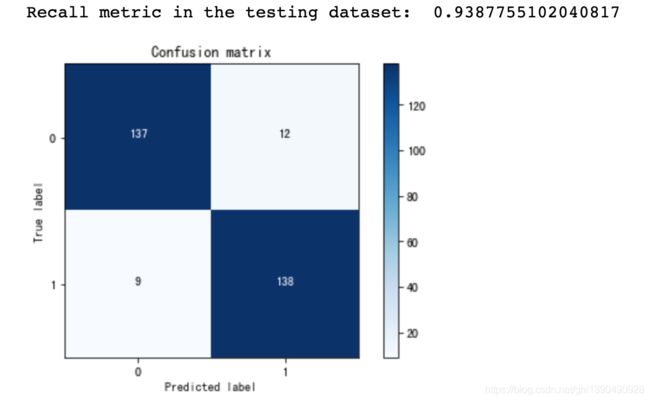
, title='Threshold >= %s'%i) Recall metric in the testing dataset: 1.0 Recall metric in the testing dataset: 1.0 Recall metric in the testing dataset: 1.0 Recall metric in the testing dataset: 0.9863945578231292 Recall metric in the testing dataset: 0.9387755102040817 Recall metric in the testing dataset: 0.891156462585034 Recall metric in the testing dataset: 0.8367346938775511 Recall metric in the testing dataset: 0.7755102040816326 Recall metric in the testing dataset: 0.5850340136054422
过采样策略
#SMOTE是过采样的一种,建议采用这种方法
import pandas as pd
from imblearn.over_sampling import SMOTE
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import train_test_split
from collections import Countercredit_cards=pd.read_csv('creditcard.csv')
columns=credit_cards.columns
# The labels are in the last column ('Class'). Simply remove it to obtain features columns
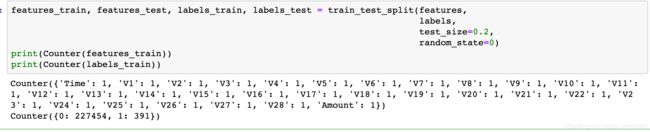
features_columns=columns.delete(len(columns)-1)
features=credit_cards[features_columns]
labels=credit_cards['Class']#该种方法不需要事先把=0的=1的单独拿出来
oversampler=SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_sample(features_train,labels_train)os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = printing_Kfold_scores(os_features,os_labels)------------------------------------------- C parameter: 0.01 ------------------------------------------- Iteration 0 : recall score = 0.8903225806451613 Iteration 1 : recall score = 0.8947368421052632 Iteration 2 : recall score = 0.968861347792409 Iteration 3 : recall score = 0.9578593332673855 Iteration 4 : recall score = 0.958397907255361 Mean recall score 0.9340356022131161 ------------------------------------------- C parameter: 0.1 ------------------------------------------- Iteration 0 : recall score = 0.8903225806451613 Iteration 1 : recall score = 0.8947368421052632 Iteration 2 : recall score = 0.9702998782781896 Iteration 3 : recall score = 0.9600795770545498 Iteration 4 : recall score = 0.9605631945131401 Mean recall score 0.9352004145192607 ------------------------------------------- C parameter: 1 ------------------------------------------- Iteration 0 : recall score = 0.8903225806451613 Iteration 1 : recall score = 0.8947368421052632 Iteration 2 : recall score = 0.9700564346575191 Iteration 3 : recall score = 0.9602994031720908 Iteration 4 : recall score = 0.9608819423835746 Mean recall score 0.9352594405927219 ------------------------------------------- C parameter: 10 ------------------------------------------- Iteration 0 : recall score = 0.8903225806451613 Iteration 1 : recall score = 0.8947368421052632 Iteration 2 : recall score = 0.970255615801704 Iteration 3 : recall score = 0.9599037161605171 Iteration 4 : recall score = 0.9607940119365582 Mean recall score 0.9352025533298407 ------------------------------------------- C parameter: 100 ------------------------------------------- Iteration 0 : recall score = 0.8903225806451613 Iteration 1 : recall score = 0.8947368421052632 Iteration 2 : recall score = 0.9705433218988603 Iteration 3 : recall score = 0.960321385783845 Iteration 4 : recall score = 0.9605961684307712 Mean recall score 0.9353040597727802 ********************************************************************************* Best model to choose from cross validation is with C parameter = 100.0 *********************************************************************************
lr = LogisticRegression(C = best_c, penalty = 'l1', solver='liblinear')
lr.fit(os_features,os_labels.values.ravel())
y_pred = lr.predict(features_test.values)
# Compute confusion matrix
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Confusion matrix')
plt.show()