卷积层和池化层的实现（使用 im2col ）

卷积

为什么卷积神经网络的能力更强？以 mnist 数据集为例，在普通的神经网络中，输入的数据是长度为 $784$ 的像素。但实际上图像本身 $28\times 28$ 的的二维结构已经被破坏了，每个像素与之上下更多像素之间的位置关系都消失了。神经网络所看见的世界是由一维向量构成的，自然无法与现实形成更好的拟合。

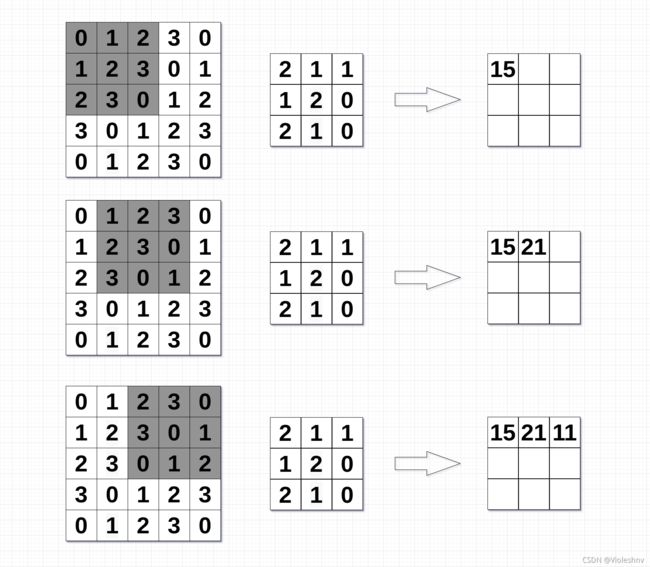
神经网络中的卷积是通过一个个滤波器对原始图像提取特征来实现的。不妨以二维单通道的图像数据为例，看看卷积的作用方式。（左侧为原始图像数据，中间为滤波器，右侧为特征图像）

原始图像的每个灰色部分都被提取出来，并与滤波器进行按位置的乘法（不是矩阵乘法），将其结果的和作为特征图像的一部分。这样就以滤波器为参照获取到了原始图像的特征，如果图像的某一部分和滤波器越相似，则获得的特征值就越大。

填充

值得注意的是，特征图像与原始图像相比小了一圈，如果经过多次卷积运算，边缘的像素可能会被忽略，同时图像的面积也在不断减小，这时可以通过一种名为**填充(padding)**的处理扩大图像，也就是在图像的四周填充 0 值。如下：

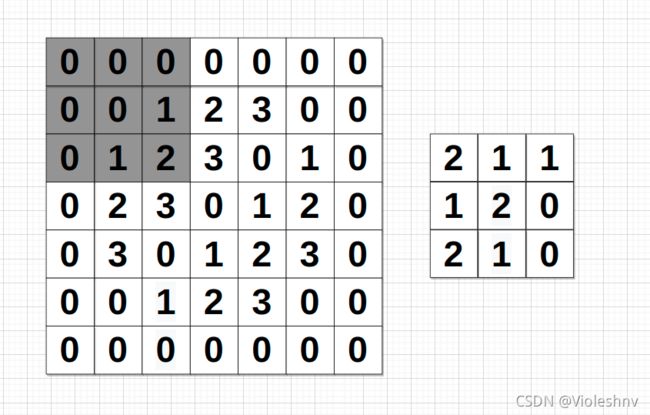
可以得到填充后的特征图像

步幅

应用滤波器的间隔称为步幅(stride)，上述的例子步幅都是 1，也就是说灰色的区域移动的长度是 1，不过也可以选取其他值。

输出大小

如果取原始图像大小为 $(H,W)$，滤波器大小为 $(FH,FW)$，填充为 $P$，步幅为 $S$，输出的特征图像大小为 $(OH,OW)$，则有
$$\begin{gathered} OH=\frac{H+2P-FH}{S}+1, \\ OW=\frac{W+2P-FW}{S}+1. \end{gathered}$$

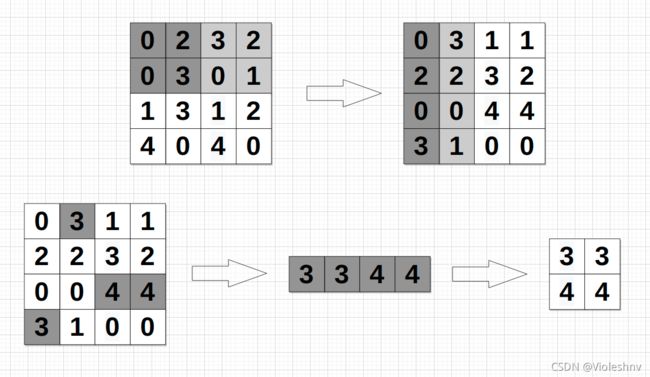
池化

池化是一种缩小特征图像大小的运算。

池化的好处主要有两个：一是在不大幅改变数据特征的情况下减少数据量，可以提高运算速度；二是将大的范围映射到小的范围可以减少扰动引起的误差。

image_to_column() 的实现

取 $N$ 为批处理数量，$C$ 为图像通道数量。

实现卷积和池化有一个相当重要的函数需要实现，这个函数可以将 $(N,C,H,W)$ 形状的四维数据转化为 $(C\times FH\times FW,N\times OH\times OW)$ 形状的数据，第一个轴与滤波器大小相同，第二个轴与输出的特征图像大小相同。

之所以要使用 image_to_column() 是为了减少 for 循环的使用，提高计算速度。

def image_to_column(data: np.ndarray, filter_h: int, filter_w: int,
                    stride: int = 1, padding: int = 0) -> np.ndarray:
    """
    assert that data.shape is (batch_num, channel, height, width)
    @params data: 4D input array
    @params filter_h, filter_w: the height and width of the filter
    @returns: the column of input array
    """
    N, C, H, W = data.shape
    assert (H + 2 * padding - filter_h) % stride == 0
    assert (W + 2 * padding - filter_w) % stride == 0
    out_h = (H + 2 * padding - filter_h) // stride + 1
    out_w = (W + 2 * padding - filter_w) // stride + 1

    im = np.pad(data, ((0, 0), (0, 0), (padding, padding), (padding, padding)),
                mode="constant")

    i0 = np.tile(np.repeat(np.arange(filter_h), filter_w), C)
    i1 = np.repeat(np.arange(out_h), out_w) * stride
    j0 = np.tile(np.arange(filter_w), filter_h * C)
    j1 = np.tile(np.arange(out_w), out_h) * stride

    i = i0.reshape(-1, 1) + i1.reshape(1, -1)
    j = j0.reshape(-1, 1) + j1.reshape(1, -1)
    k = np.repeat(np.arange(C), filter_h * filter_w).reshape(-1, 1)

    col = im[:, k, i, j]
    col = col.transpose(1, 2, 0).reshape(filter_h * filter_w * C, -1)
    return col

卷积的过程

我们通过矩阵的维数和轴来观察卷积的过程：

$$\begin{gathered} \stackrel{\text{原始数据}}{(N,C,H,W)}image\_to\_col\stackrel{\text{col}}{(C\times FH\times FW,N\times OH\times OW)}, \\ \stackrel{\text{滤波器}}{(FN,C,FH,FW)}reshape\stackrel{\text{col\_f}}{(FN,C\times FH\times FW)}, \\ \stackrel{\text{矩阵乘法}}{\underset{\text{col\_f}}{(FN,C\times FH\times FW)}\cdot \underset{\text{col}}{(C\times FH\times FW,N\times OH\times OW)}}+b \\ \to \stackrel{\text{特征图像(2维)}}{(FN,N\times OH\times OW)} \\ reshape\stackrel{\text{特征图像(4维)}}{(FN,N,OH,OW)} \\ FN\to C_{next}\stackrel{\text{特征图像’(4维)}}{(C_{next},N,OH,OW)} \\ transpose\stackrel{\text{下一个原始数据(未激活)}}{(N,C_{next},OH,OW)} \\ activation\stackrel{\text{下一个原始数据}}{(N,C_{next},OH,OW)}. \end{gathered}$$

注：图中出现的字母均按维度排列

其中，$C\times FH\times FW$ 就是滤波器作用的大小，作用方式和神经网络相同，使用矩阵乘法之后在加上一个偏置就可以获得输出矩阵。此时这个输出矩阵的维度和轴还需要进一步调整，第一步是通过 reshape 产生四个轴，与原数据相同；然后将 $FN$ 解读为下一个输入的通道数 $C_{next}$，再变更轴的排列顺序；最后再使用一个激活函数，卷积就大功告成了。

可以将 reshape 函数的作用方式理解为将多个轴合并到一个轴上，或将一个轴分解到多个轴上，但分解和合并不能改变原有轴的排列顺序。比如将 $(C\times FH\times FW)$ 重组为 $(C,FH,FW)$ 是正确的，但是重组为 $(FH,FW,C)$ 就是错误的。虽然从数值上看是可行的，但实际上破坏了数据的立体结构。

通过一个例子将理论变为实际的代码：

a = np.array([[0, 1, 2, 3, 0],
              [1, 2, 3, 0, 1],
              [2, 3, 0, 1, 2],
              [3, 0, 1, 2, 3],
              [0, 1, 2, 3, 0]]).reshape(1, 1, 5, 5)
N, C, H, W = a.shape

f = np.array([
    [
        [2, 1, 1],
        [1, 2, 0],
        [2, 1, 0]
    ],
    [
        [1, 0, 2],
        [1, 1, 0],
        [1, 2, 2]
    ]
]).reshape(2, 1, 3, 3)
FN, FC, FH, FW = f.shape

assert FC == C

stride, padding = 1, 1

col = image_to_column(a, 3, 3, stride=stride, padding=padding)  # col
col_f = f.reshape(FN, -1)                                       # col_f

out_h = (H + 2 * padding - FH) // stride + 1
out_w = (W + 2 * padding - FW) // stride + 1
out = np.dot(col_f, col)                                      # 矩阵乘法
out = out.reshape(FN, N, out_h, out_w).transpose(1, 0, 2, 3)  # reshape & transpose

可以获得卷积层的实现

class Convolution:

    def __init__(self, w, b, stride, padding):
        self.w = w
        self.b = b
        self.stride = stride
        self.padding = padding

    def forward(self, data):
        FN, FC, FH, FW = self.w.shape
        N, C, H, W = data.shape
        assert FC == C

        col = image_to_column(data, FH, FW,
                              stride=self.stride, padding=self.padding)
        col_f = self.w.reshape(FN, -1)

        out_h = (H + 2 * self.padding - FH) // self.stride + 1
        out_w = (W + 2 * self.padding - FW) // self.stride + 1

        out = np.dot(col_f, col) + self.b
		out = out.reshape(FN, N, out_h, out_w).transpose(1, 0, 2, 3)

        return out

注意此时我们将图像展开成二维数据时并没有丢失图像本身的立体结构，而是为了计算的方便而做的。

池化的过程

池化可以理解为一种特殊的卷积，只不过它的滤波器的作用是提取最大值或平均值。

依旧通过矩阵的维数和轴来观察池化的过程：
$$\begin{gathered} \stackrel{\text{原始数据 im}}{(N,C,H,W)} \\ image\_to\_col\stackrel{\text{col}}{(C\times FH\times FW,N\times OH\times OW)} \\ reshape\stackrel{\text{展开}}{(C,FH\times FW,N\times OH\times OW)} \\ max\stackrel{\text{池化图像(2维)}}{(C,1,N\times OH\times OW)} \\ reshape\stackrel{\text{池化图像(4维)}}{(C,N,OH,OW)} \\ transpose\stackrel{\text{下一个原始数据(未激活)}}{(N,C,OH,OW)} \\ activation\stackrel{\text{下一个原始数据}}{(N,C,OH,OW)}. \end{gathered}$$

注：图中出现的字母均按维度排列

前面已经说过可以将池化层的理解为取最大值的卷积，不过这个时候我们要保留通道 $C$，只对 $FH\times FW$ 这块使用池化。所以通过 reshape 将 $FH\times FW$ 暴露出来，再对这个轴使用 max(axis=1)，将 $FH\times FW$ “压缩”到一个最大值，再同卷积一样调整一些维数和轴就可以了。

可以获得池化层的实现

class Pooling:

    def __init__(self, h, w, stride, padding):
        self.h = h
        self.w = w
        self.stride = stride
        self.padding = padding

    def forward(self, data):
        N, C, H, W = data.shape

        out_h = (H - self.h) // self.stride + 1
        out_w = (W - self.w) // self.stride + 1

        col = image_to_column(data, self.h, self.w,
                              stride=self.stride, padding=self.padding)
        col = col.reshape(C, self.h * self.w, -1)

        out = np.max(col, axis=1)
        out = out.reshape(C, N, out_h, out_w).transpose(1, 0, 2, 3)

        return out