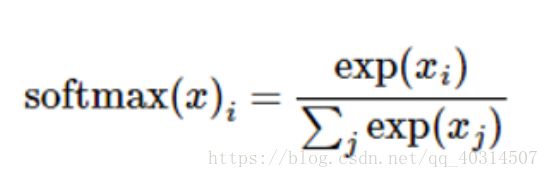【tensorflow 深度学习】2.非线性回归与Mnist数据集分类

1.非线性回归例子

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

#使用numpy生成200个随机点
x_data=np.linspace(-0.5,0.5,200)[:,np.newaxis]#增加一个维度  使其成为200行1列
noise=np.random.normal(0,0.02,x_data.shape)#生成一些干扰项,形状和x_data一样
y_data=np.square(x_data)+noise

#定义两个placeholder
x=tf.placeholder(tf.float32, [None,1])  #行数不确定，1列
y=tf.placeholder(tf.float32, [None,1])

#定义神经网络中间层
Weights_L1=tf.Variable(tf.random_normal([1,10]))
biases_L1=tf.Variable(tf.zeros([1,10]))
Wx_plus_b_L1=tf.matmul(x,Weights_L1)+biases_L1
L1=tf.nn.tanh(Wx_plus_b_L1)

#定义神经网络输出层
Weights_L2=tf.Variable(tf.random_normal([10,1]))
biase_L2=tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2=tf.matmul(L1,Weights_L2)+biase_L2
prediction=tf.nn.tanh(Wx_plus_b_L2)

#二次代价函数
loss=tf.reduce_mean(tf.square(y-prediction))
#使用梯度下降法训练
train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)

with tf.Session() as sess:
    #变量初始化
    sess.run(tf.global_variables_initializer())
    for _ in range(2000):
        sess.run(train_step,feed_dict={x:x_data,y:y_data})
        
    #获得预测值
    prediction_value=sess.run(prediction,feed_dict={x:x_data})
    #画图
    plt.figure()
    plt.scatter(x_data,y_data)
    plt.plot(x_data,prediction_value,'r-',lw=5) #线宽为5
    plt.show()

结果：

2.手写数字训练集和softmax函数用法

    (1).MNIST下载下来的数据集被分成两部分：60000行的训练数据集（mnist.train）和10000行的测试数据集（mnist.test）

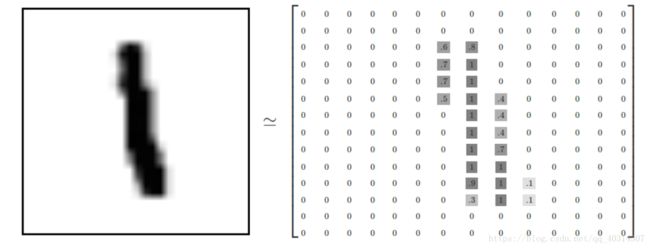
每一张图片包含28*28个像素，我们把这一个数组展开成一个向量，长度是28*28=784。因此在MNIST训练数据集中

mnist.train.images 是一个形状为 [60000, 784] 的张量，第一个维度数字用来索引图片，第二个维度数字用来索引每张图片中

的像素点。图片里的某个像素的强度值介于0-1之间。

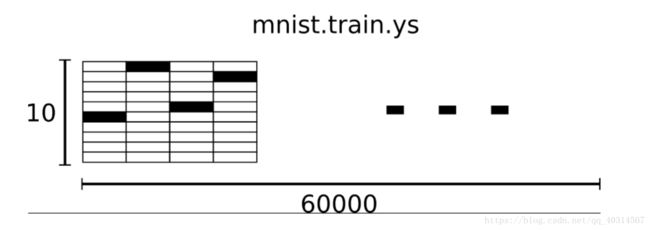
MNIST数据集的标签是介于0-9的数字，我们要把标签转化为“one-hot vectors” 。一个onehot向量除了某一位数字是1以

外，其余维度数字都是0，比如标签0将表示为([1,0,0,0,0,0,0,0,0,0])，标签3将表示为([0,0,0,1,0,0,0,0,0,0]) 。

因此， mnist.train.labels 是一个 [60000, 10] 的数字矩阵。

    (2)神经网络构建

                                    

    (3)softmax函数

    我们知道MNIST的结果是0-9，我们的模型可能推测出一张图片是数字9的概率是80%，是数字8的概率是10%，然后其他数字

的概率更小，总体概率加起来等于1。这是一个使用softmax回归模型的经典案例。 softmax模型可以用来给不同的对象分配概

率。

                            

比如输出结果为[1,5,3]

         

    （4）.mnist数据集分类简单版本

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import  input_data

#载入数据集
mnist=input_data.read_data_sets("MNIST_data",one_hot=True)

#每个批次的大小
batch_size=100
#计算一共有多少个批次
n_batch=mnist.train.num_examples//batch_size

#定义两个placeholder
x=tf.placeholder(tf.float32, [None,784])
y=tf.placeholder(tf.float32,[None,10])

#创建一个简单的神经网络
W=tf.Variable(tf.zeros([784，10]))
b=tf.Variable(tf.zeros([10]))
prediction=tf.nn.softmax(tf.matmul(x,W)+b)

#二次代价函数
loss=tf.reduce_mean(tf.square(y-prediction))
#使用梯度下降法
train_step=tf.train.GradientDescentOptimizer(0.2).minimize(loss)
#初始化变量
init=tf.global_variables_initializer()

#结果存放在一个布尔型列表中

correct_prediction = tf.equal(tf.argmax(y,1),tf.argmax(prediction,1))#argmax返回一维张量中最大的值所在的位置
#求准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction,tf.float32))
with tf.Session() as sess:
    sess.run(init)
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs,batch_ys =  mnist.train.next_batch(batch_size)
            sess.run(train_step,feed_dict={x:batch_xs,y:batch_ys})
        
        acc = sess.run(accuracy,feed_dict={x:mnist.test.images,y:mnist.test.labels})
        print("Iter " + str(epoch) + ",Testing Accuracy " + str(acc))

结果：

    

程序可优化的地方：

    1.batch_size大小可以修改

    2.增加隐藏层

    3.权值和偏侧值的初始化方式

    4.代价函数修改

    5.学习率修改，优化方式修改

    6.训练次数修改