线性回归csv数据集_【Python数据科学手册】专题：线性回归

线性回归模型是解决回归任务的好起点。

你可能对线性回归模型最简单的形式(即对数据拟合一条直线)已经很熟悉了，不过经过扩展，这些模型可以对更复杂的数据行为进行建模。

首先导入常用的程序库：

%matplotlib inlineimport matplotlib.pyplot as pltimport seaborn as sns; sns.set()import numpy as np

01

 简单线性回归

首先来介绍最广为人知的线性回归模型——将数据拟合成一条直线。直线拟合的模型方程为y=ax+by=ax+b，其中aa是直线斜率，bb是直线截距。

下面的数据，它们是从斜率为2、截距为-5 的直线中抽取的散点

rng = np.random.RandomState(1)x = 10 * rng.rand(50)y = 2 * x - 5 + rng.randn(50)plt.scatter(x, y);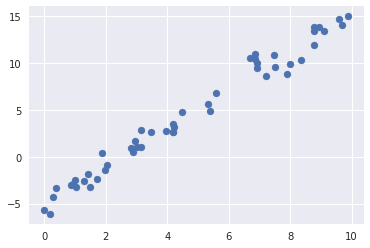

用Scikit-Learn 的LinearRegression 评估器来拟合数据，并获得最佳拟合直线

from sklearn.linear_model import LinearRegressionmodel = LinearRegression(fit_intercept=True)model.fit(x[:, np.newaxis], y)xfit = np.linspace(0, 10, 1000)yfit = model.predict(xfit[:, np.newaxis])plt.scatter(x, y)plt.plot(xfit, yfit);

数据的斜率和截距都在模型的拟合参数中，Scikit-Learn 通常会在参数后面加一条下划线，即coef_ 和intercept_：

print("Model slope:    ", model.coef_[0])print("Model intercept:", model.intercept_)

可以看到，拟合结果与真实值非常接近。

LinearRegression 评估器能做的可远不止这些——除了简单的直线拟合，它还可以处理多维度的线性回归模型：

y=a₀+a₁x₁+a₂x₂+⋯

里面有多个x 变量。从几何学的角度看，这个模型是拟合三维空间中的一个平面，或者是为更高维度的数据点拟合一个超平面。

rng = np.random.RandomState(1)X = 10 * rng.rand(100, 3)y = 0.5 + np.dot(X, [1.5, -2., 1.])model.fit(X, y)print(model.intercept_)print(model.coef_)

0.5
[ 1.5 -2.   1. ]

其中y 变量是由3个随机的x变量线性组合而成，线性回归模型还原了方程的系数。

通过这种方式，就可以用一个LinearRegression 评估器拟合数据的回归直线、平面和超平面了。

局限性： 变量限制在线性关系上

02

基函数回归

可以通过基函数对原始数据进行变换，从而将变量间的线性回归模型转换为非线性回归模型。

这个方法的多维模型是：y=a₀+a₁x₁+a₂x₂+a₃x₃+⋯

其中一维的输入变量xx转换成了三维变量x₁,x₂,x₃。让x_n=f_n(x)，这里的f_n(x)是转换数据的函数。

假如f_n(x)=xⁿ，那么模型就会变成多项式回归：y=a₀+a₁x+a₂x²+a₃x³+⋯

需要注意的是，这个模型仍然是一个线性模型，也就是说系数a_n彼此不会相乘或相除。

1、多项式函数

多项式投影非常有用，因此Scikit-Learn 内置了PolynomialFeatures 转换器实现这个功能：

from sklearn.preprocessing import PolynomialFeaturesx = np.array([2, 3, 4])poly = PolynomialFeatures(3, include_bias=False)poly.fit_transform(x[:, None])

转换器通过指数函数，将一维数组转换成了三维数组。这个新的高维数组之后可以放在多项式回归模型中。

我们创建一个7 次多项式回归模型：

from sklearn.pipeline import make_pipelinepoly_model = make_pipeline(PolynomialFeatures(7),                           LinearRegression())

数据经过转换之后，我们就可以用线性模型来拟合x 和y 之间更复杂的关系了。

rng = np.random.RandomState(1)x = 10 * rng.rand(50)y = np.sin(x) + 0.1 * rng.randn(50)poly_model.fit(x[:, np.newaxis], y)yfit = poly_model.predict(xfit[:, np.newaxis])plt.scatter(x, y)plt.plot(xfit, yfit);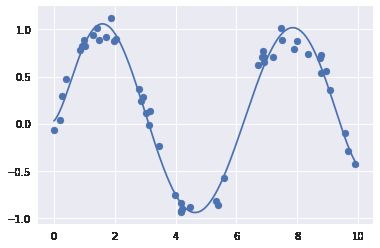

通过运用7 次多项式基函数，这个线性模型可以对非线性数据拟合出极好的效果！

2. 高斯基函数

例如，有一种常用的拟合模型方法使用的并不是一组多项式 基函数，而是一组高斯基函数。

图中的阴影部分代表不同规模基函数，把它们放在一起时就会产生平滑的曲线。

from sklearn.base import BaseEstimator, TransformerMixinclass GaussianFeatures(BaseEstimator, TransformerMixin):    """Uniformly spaced Gaussian features for one-dimensional input"""        def __init__(self, N, width_factor=2.0):        self.N = N        self.width_factor = width_factor        @staticmethod    def _gauss_basis(x, y, width, axis=None):        arg = (x - y) / width        return np.exp(-0.5 * np.sum(arg ** 2, axis))            def fit(self, X, y=None):        # create N centers spread along the data range        self.centers_ = np.linspace(X.min(), X.max(), self.N)        self.width_ = self.width_factor * (self.centers_[1] - self.centers_[0])        return self            def transform(self, X):        return self._gauss_basis(X[:, :, np.newaxis], self.centers_,                                 self.width_, axis=1)    gauss_model = make_pipeline(GaussianFeatures(20),                            LinearRegression())gauss_model.fit(x[:, np.newaxis], y)yfit = gauss_model.predict(xfit[:, np.newaxis])plt.scatter(x, y)plt.plot(xfit, yfit)plt.xlim(0, 10);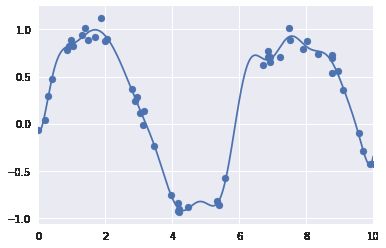

03

正则化

虽然在线性回归模型中引入基函数会让模型变得更加灵活，但是也很容易造成过拟合。例如，如果选择了太多高斯基函数，那么最终的拟合结果看起来可能并不好。

model = make_pipeline(GaussianFeatures(30),                      LinearRegression())model.fit(x[:, np.newaxis], y)plt.scatter(x, y)plt.plot(xfit, model.predict(xfit[:, np.newaxis]))plt.xlim(0, 10)plt.ylim(-1.5, 1.5);

如果将数据投影到30 维的基函数上，模型就会变得过于灵活，从而能够适应数据中不同位置的异常值。如果将高斯基函数的系数画出来，就可以看到过拟合的原因。

def basis_plot(model, title=None):    fig, ax = plt.subplots(2, sharex=True)    model.fit(x[:, np.newaxis], y)    ax[0].scatter(x, y)    ax[0].plot(xfit, model.predict(xfit[:, np.newaxis]))    ax[0].set(xlabel='x', ylabel='y', ylim=(-1.5, 1.5))        if title:        ax[0].set_title(title)    ax[1].plot(model.steps[0][1].centers_,               model.steps[1][1].coef_)    ax[1].set(xlabel='basis location',              ylabel='coefficient',              xlim=(0, 10))    model = make_pipeline(GaussianFeatures(30), LinearRegression())basis_plot(model)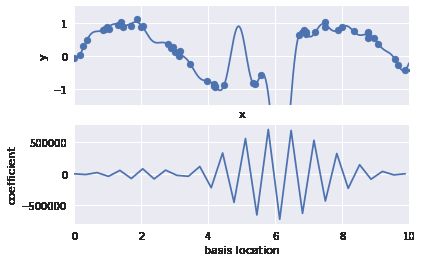

下面那幅图显示了每个位置上基函数的振幅。当基函数重叠的时候，通常就表明出现了过拟合：相邻基函数的系数相互抵消。这显然是有问题的，如果对较大的模型参数进行惩罚(penalize)，从而抑制模型剧烈波动，应该就可以解决这个问题了。这个惩罚机制被称为正则化(regularization)，有几种不同的表现形式。

1. 岭回归(L2范数正则化)

正则化最常见的形式可能就是岭回归(ridge regression，或者L2 范数正则化)，有时也被称为吉洪诺夫正则化(Tikhonov regularization)。其处理方法是对模型系数平方和(L2 范数)进行惩罚，模型拟合的惩罚项为：

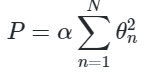
α 是一个自由参数，用来控制惩罚的力度。这种带惩罚项的模型内置在Scikit-Learn的Ridge 评估器中

from sklearn.linear_model import Ridgemodel = make_pipeline(GaussianFeatures(30), Ridge(alpha=0.1))basis_plot(model, title='Ridge Regression')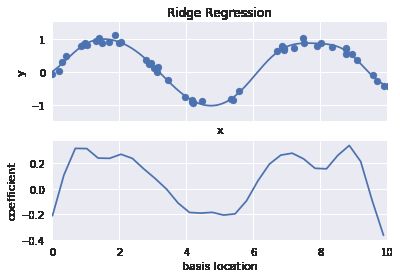

参数α 是控制最终模型复杂度的关键。如果α → 0，那么模型就恢复到标准线性回归结果；如果α → ∞，那么所有模型响应都会被压制。

2. Lasso正则化(L1范数)

另一种常用的正则化被称为Lasso，其处理方法是对模型系数绝对值的和(L1 范数)进行惩罚:

虽然它在形式上非常接近岭回归，但是其结果与岭回归差别很大。例如，由于其几何特性，Lasso 正则化倾向于构建稀疏模型；也就是说，它更喜欢将模型系数设置为0。

模型系数的L1- 范数正则化实现的

from sklearn.linear_model import Lassomodel = make_pipeline(GaussianFeatures(30), Lasso(alpha=0.001))basis_plot(model, title='Lasso Regression')

04

案例：预测自行车流量

首先加载两个数据集，用日期作索引:

import pandas as pdcounts = pd.read_csv('datalab/5666/FremontBridge.csv', index_col='Date', parse_dates=True)weather = pd.read_csv('datalab/5666/BicycleWeather.csv', index_col='DATE', parse_dates=True)

计算每一天的自行车流量，将结果放到一个新的DataFrame中

daily = counts.resample('d').sum()daily['Total'] = daily.sum(axis=1)daily = daily[['Total']] # remove other columns

我们发现同一周内每一天的模式都是不一样的。因此，我们在数据中加上7 列0~1 值表示星期几:

days = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']for i in range(7):    daily[days[i]] = (daily.index.dayofweek == i).astype(float)

我们觉得骑车人数在节假日也有所变化。因此，再增加一列表示当天是否为节假日:

from pandas.tseries.holiday import USFederalHolidayCalendarcal = USFederalHolidayCalendar()holidays = cal.holidays('2012', '2016')daily = daily.join(pd.Series(1, index=holidays, name='holiday'))daily['holiday'].fillna(0, inplace=True)

我们还认为白昼时间也会影响骑车人数。因此，用标准的天文计算来添加这列信息:

def hours_of_daylight(date, axis=23.44, latitude=47.61):    """Compute the hours of daylight for the given date"""    days = (date - pd.datetime(2000, 12, 21)).days    m = (1. - np.tan(np.radians(latitude))         * np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25)))    return 24. * np.degrees(np.arccos(1 - np.clip(m, 0, 2))) / 180.daily['daylight_hrs'] = list(map(hours_of_daylight, daily.index))daily[['daylight_hrs']].plot()plt.ylim(8, 17)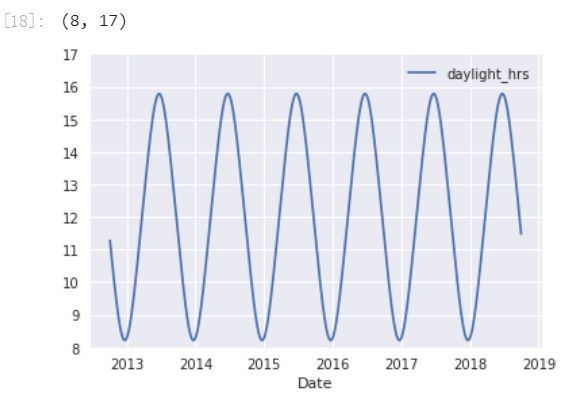

我们还可以增加每一天的平均气温和总降雨量。除了降雨量的数值之外，再增加一个标记表示是否下雨(是否降雨量为0)

# 温度是按照1/10摄氏度统计的，首先转换为摄氏度weather['TMIN'] /= 10weather['TMAX'] /= 10weather['Temp (C)'] = 0.5 * (weather['TMIN'] + weather['TMAX'])# precip is in 1/10 mm; convert to inchesweather['PRCP'] /= 254weather['dry day'] = (weather['PRCP'] == 0).astype(int)daily = daily.join(weather[['PRCP', 'Temp (C)', 'dry day']])

最后，增加一个从1 开始递增的计数器，表示一年已经过去了多少天。这个特征可以让我们看到每一年自行车流量的增长或减少：

daily['annual'] = (daily.index - daily.index[0]).days / 365.

数据已经准备就绪，来看看前几行：

daily.head()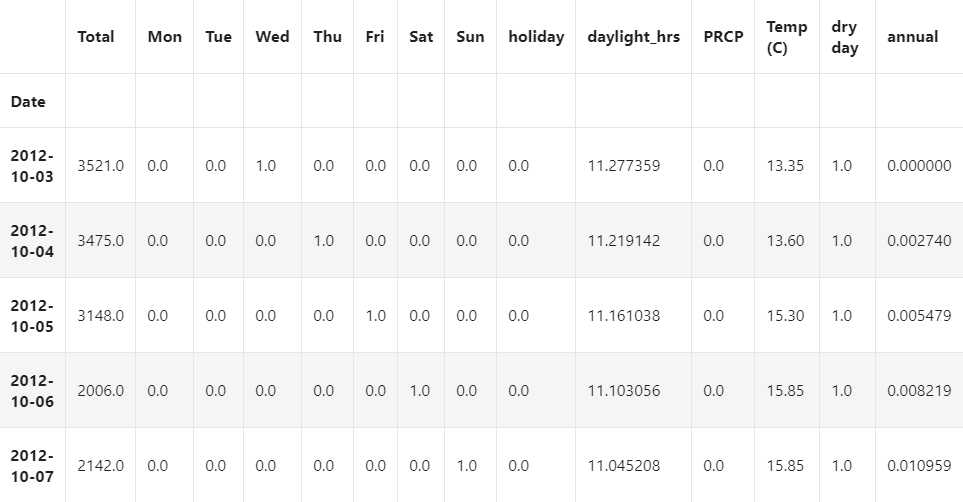

有了这些数据之后，就可以选择需要使用的列，然后对数据建立线性回归模型。我们不在模型中使用截距，而是设置fit_intercept = False，因为每一天的总流量(Total 字段)基本上可以作为当天的截距。

# Drop any rows with null valuesdaily.dropna(axis=0, how='any', inplace=True)column_names = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun', 'holiday',                'daylight_hrs', 'PRCP', 'dry day', 'Temp (C)', 'annual']X = daily[column_names]y = daily['Total']model = LinearRegression(fit_intercept=False)model.fit(X, y)daily['predicted'] = model.predict(X)

最后，对比自行车真实流量(Total 字段)与预测流量(predicted 字段)

daily[['Total', 'predicted']].plot(alpha=0.5);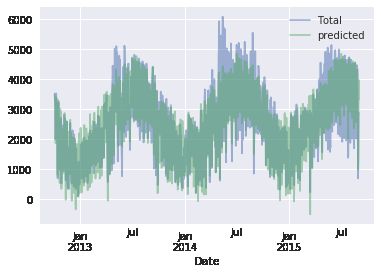

显然，我们丢失了一些关键特征，尤其是夏天的预测数据。要么是由于特征没有收集全(即可能还有其他因素会影响人们是否骑车)，要么是有一些非线性关系我们没有考虑到(例如，可能人们在温度过高或过低时都不愿意骑车)

评估各个特征对每日自行车流量的影响：

params = pd.Series(model.coef_, index=X.columns)params

如果不对这些数据的不确定性进行评估，那么它们很难具有解释力。可以用自举重采样方法快速计算数据的不确定性：

from sklearn.utils import resamplenp.random.seed(1)err = np.std([model.fit(*resample(X, y)).coef_              for i in range(1000)], 0)

有了估计误差之后，再来看这些结果：

print(pd.DataFrame({'effect': params.round(0),                    'error': err.round(0)}))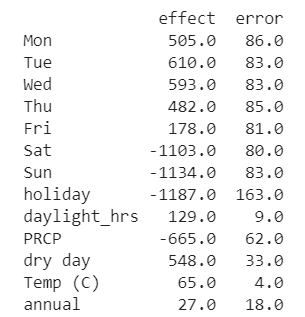

首先，星期特征是比较稳定的，工作日骑车的人数显然比周末和节假日要多。其次，白昼时间每增加1 小时，就平均增加129 ± 9 个骑车的人；而温度每上升1 度，则增加65 ± 4 个骑车的人；如果那天没下雨，那么骑车人数增加546 ± 33 人；降雨量每增加1 英寸，骑车人数减少665 ± 62 人。当所有影响因素都生效之后，一年中每多一天骑车人数增加(日环比增幅)28 ± 18 人。

我们的模型的确丢失了一些重要信息。例如，变量的非线性影响因素(例如降雨和寒冷天气的影响)和非线性趋势(例如人们在温度过高或过低时可能都不愿意骑车)在模型中都没有体现。另外，我们丢掉了一些细颗粒度的数据(例如下雨天的早晨和下雨天的傍晚之间的差异)，还忽略了相邻日期彼此间的相关性(例如下雨的星期二对星期三骑车人数的影响，或者滂沱大雨之后意外的雨过天晴对骑车人数的影响)，这些都可能对骑车人数产生影响。现在你手上已经有了工具，如果愿意，可以进一步进行分析。

点击下方图片即可阅读

那么如何了解线性回归的原理和算法呢？

分类算法评估中的“它们”有什么用处？

学好Scikit-Learn，

于是你默默地推了一下酷酷的墨镜【上篇】

学会PyTorch，你就是这条街上最靓的仔~

如果你也有想分享的干货，可以登录天池实验室(notebook)，包括赛题的理解、数据分析及可视化、算法模型的分析以及一些核心的思路等内容。

小天会根据你分享内容的数量以及程度，给予丰富的神秘天池大礼以及粮票奖励。分享成功后你也可以通过下方钉钉群?主动联系我们的社区运营同学(钉钉号： yiwen1991)

天池宝贝们有任何问题，可在戳“留言”评论或加入钉钉群留言，小天会认真倾听每一个你的建议！

?