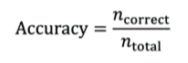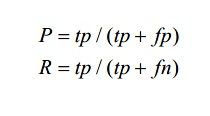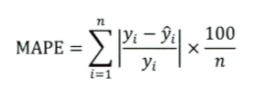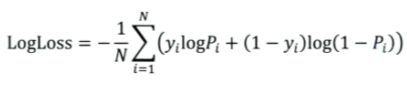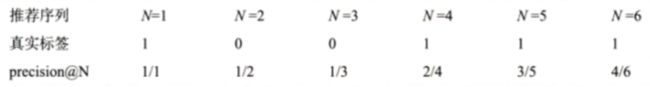推荐系统(Recommender System)笔记 05:推荐系统的评估
推荐系统(Recommender System)05:推荐系统的评估
- 离线评估方法与基本评价指标
-
- 离线评估的主要方法
-
- Holdout 检验
- 交叉验证 (Cross Validation)
- 自助法 (Bootstrap)
- 离线评估的指标
-
- 准确率 (Accuracy)
- 正确率 (Precision) 和召回率 (Recall)
- 均方根误差 (RMSE)
- 对数损失函数 (LogLoss)
- 直接评估推荐序列的离线指标
-
- P-R 曲线
- ROC 曲线
- 平均精度均值(mAP)
- 更接近线上环挠的离线评估方法 - Replay
-
- 动态离线评估方法
- Netflix 的 Replay 评估方法实现
- A/B 测试与线上评估指标
-
- A/B 测试的分组思想
- A/B 测试的线上评估指标
- A/B 测试的问题
- 快速线上评估方法 - Interleaving
-
- Interleaving 的实现
- “灵敏度” 比较
- Interleaving 指标与 A/B 测试指标的相关性
- Interleaving 的优缺点
- 推荐系统的评估体系
和所有机器学习任务一样,为推荐系统确立一个评估指标是非常有必要的。这是因为评估的指标可以直接衡量推荐系统的优化方向是否合理,是否符合商业的预期。另外,如果还有印象,我们在之前说过,确立一个合理的优化目标会让研发和业务部门配合得更好。那么对于这个优化目标得评估自然也能加强团队之间得协作。
下面,我们将从离线评估到线上评估,从各个不同的层级来逐一分析
离线评估方法与基本评价指标
离线评估是最基本的评估方法 。顾名思义,离线评估就是在将模型部署于线上环境之前,在离线环境中进行评估。这一评估方法的优点在于无须浪费线上资源,远离线上工作环境更为安全,非常适合对全量训练进行评估。
离线评估的主要方法
Holdout 检验
这是所有机器学习离线评估中最基本的方法,即将数据随机划分为训练集和测试集,用训练集训练模型,使用测试机来测试模型的效果。
这一方法的缺点在于测试集的测试结果与数据划分的方式直接相关。如果仅仅进行少量的 Holdout 检验,结果的随机性会比较大。
交叉验证 (Cross Validation)
这一方法可以有效消除 Holdout 检验结果的随机性。最经典的就是 k-fold 交叉验:
首先将数据划分为训练集和测试集,之后,将训练集划分为 k 等份。进行 k 次迭代,每次迭代取其中一份训练数据作为验证集,剩下 (k - 1) 份数据作为训练集。每轮中的用 1 份验证集得出的评估结果最后进行平均,得到最后的评估结果。而 Leave 1 out 则是 k-fold 的一种特例,即每次只用一个样本作为验证集
自助法 (Bootstrap)
Holdout 和交叉验证都需要对数据集进行分割,但如果原本数据集就比较小,进行分割之后,训练集会很不足。这时就需要使用自助法 (Bootstrap),该方法实质上是集成学习的一种思想:
对于有 n 个样本的数据集,有放回地采样 n 次,得到规模为 n 的训练集,很显然,此时训练集中会有重复的数据。而那些在整个过程中从未被采样过的数据自然就成了测试集。
这种不求分割的方法就是所谓的自助法
离线评估的指标
离线评估的指标和基本的机器学习模型评估指标基本一致
准确率 (Accuracy)
指分类正确的样本占总样本个数的比例:
这是最常见和最符合直觉的指标。但是这个指标在不同类的样本比例非常不协调时,会有比较严重的问题。 比如 100 个样本,其中共有 90 个负样本,那模型即使将所有样本都分类为负样本,那也会有 90% 的正确率,但此时该模型很可能是有严重缺陷的。
正确率 (Precision) 和召回率 (Recall)
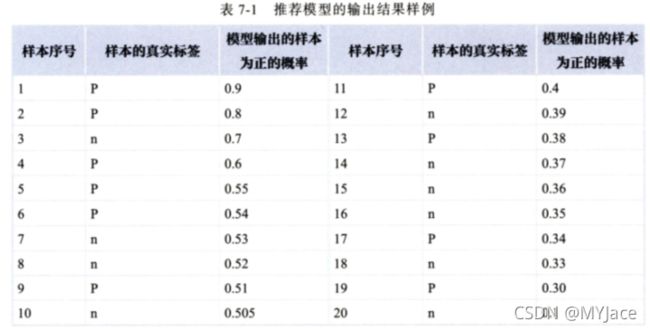
再一次拿出 Confusion Matrix:
简而言之,正确率 (Precision) 就是找回来的结果里有多少是正确的,召回率 (Recall) 就是正确的结果我们找回来多少。 在推荐系统中,我们会将在最后 Top N 推荐结果中的对象视为 “正样本”,以此计算正确率和召回率
为了综合反映 Precision 和 Recall,可以选择 F1-Score 这个指标作为评估指标:
均方根误差 (RMSE)
RMSE 常用来评估回归模型的性能。当我们选择使用 CTR 预估模型来构建推荐系统时,推荐系统实际上预测的是对象为正样本(值得推荐对象)的概率,此时就可以使用 RMSE 这个指标:
RMSE 能够很好地反映回归模型预测值与真实值的偏离程度。但是如果有一个离群点 (Outlet) 距离预测曲线距离非常远,会极大影响 RMSE 的可靠性。此时就可以选择鲁棒性更强的平均绝对百分比误差 (Mean Absolute Percent Error, MAPE) 来作为评估指标:
MAPE 就相当于将每个点预测值与真实值之间的误差进行了归一化,降低个别离群点带来的影响。
对数损失函数 (LogLoss)
对于一个二分类问题,对数损失函数 (LogLoss) 如下所示:
yi 是样本 xi 的真实标签,pi 是预测 xi 为正样本的概率。实际上 LogLoss 就是逻辑回归 (LR) 的损失函数。我们在之前介绍深度推荐模型时已经知道,不少模型的输出层就是 LR 层或者 softmax,因此这个指标能够非常直观地反映模型损失函数的变化
直接评估推荐序列的离线指标
之前介绍的几种离线评估指标都是将推荐模型看作一个 CTR 预估模型,也就是说,模型最终得出的是一个预测的点击率。然而真正的推荐系统最后给出的应该是一个推荐列表,由 Top K 推荐对象组成的推荐列表。
所以,评估推荐系统的最直观的方法应该是直接对这样一个推荐序列进行评估。
P-R 曲线
所谓的 P-R 曲线就是 Precision-Recall 曲线,其横坐标就是 Recall,纵坐标就是 Precision。对于一个排序模型,该曲线以如下形式进行解释:
“该曲线上的某个点表示在某一个阈值下,模型将大于该阈值的结果判定为正样本,将小于的判定为负样本时,排序结果对应的正确率和召回率”
整条 P-R 曲线是通过从高到低移动正样本阈值生成的:
在召回率接近 0 时, 模型 A 的正确率是 0.9 ,模型 B 的正确率是 1 ,这说明模型 B 中得分前几位的样本全部是真正的正样本,而模型 A 中即使是得分最高的几个样本,也存在预测错误的情况。 然而,随着召回率的增加, 正确率整体上有所下降。在召回率为 1 时, 模型 A 的正确率反而超过了模型 B。这充分说明 , 只用一个点的精确率和召回率是不能全面衡量模型性能的,只有通过 P-R 曲线的整体表现,才能对模型进行更全面的评估
对于绘制好的 P-R 曲线,其 AUC (Area Under Curve) 即曲线下的面积可以衡量 P-R 曲线的优劣,AUC 越大,表明排序模型的性能越好
ROC 曲线
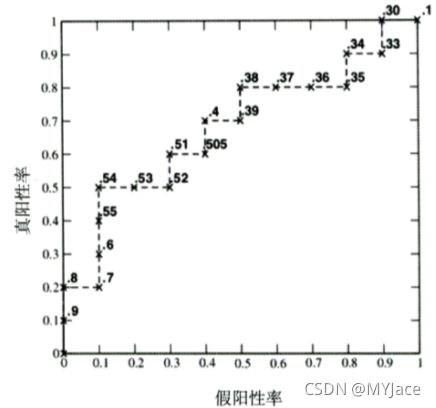
ROC 曲线的全称是 the Receiver Operating Characteristic 曲线 , 中文译为"受试者工作特征曲线"。该曲线的横坐标为 FPR (False Positive Rate,假阳率),纵坐标为 TPR (True Positive Rate,真阳率):
其中,P 是真实的正样本数量 , N 是真实的负样本数量。同 P-R 曲线一样 , ROC 曲线也是通过不断移动模型正样本阈值生成的。这一过程实际上就是不断降低阈值的过程。
以上面的这 20 个样本为例,最初阈值为无穷大,此时所有预测概率皆小于该阈值,因此所有样本都会预测为负,此时 FPR 和 TPR 皆为 0,对应曲线的零点;接下来阈值减小,当与之为 0.9 时,仅有第一个样本大于等于阈值,因此被判断为正样本,其余 19 个样本都是负样本,此时 FP = 0,TP = 1,所以 FPR = 0,TPR = 1/10 = 0.1,对应曲线的 (0, 0.1) 点。以此类推,不断降低阈值,可以得到如下所示的 ROC 曲线:
对于 ROC 曲线,同样使用 AUC 计算曲线下面积进行优劣衡量。
平均精度均值(mAP)
平均精度均值 (mean Average Precision),这个值实际上是对平均精度 (Average Precision) 进行再次平均得到的。
看一个具体的例子:
此时 AP (Average Precision) = (1 + 2/4 + 3/5 + 4/6) / 4 = 0.6917。在推荐系统中,会对每一位用户都生成一个推荐序列,因此,每个用户都有各自的 AP,对这些 AP 再进行平均即可得到 mAP。
需要注意的是 mAP 是对每个用户的样本进行分用户排序,而 P-R 曲线和 ROC 曲线则是对全量测试样本进行排序。 这一点在实际操作中需要格外注意。
在实际项目中,需要根据需求选择合适的 2~4 个指标进行综合考量,切忌在某个指标上钻牛角尖。
更接近线上环挠的离线评估方法 - Replay
目前我们已经了解了离线评估的方法以及使用的指标,但是我们要知道,最终训练好的模型都是要放在线上提供服务,创造营收的。所以离线评估的结果应该越接近线上评估越好。 要达到这个目标,就应该让离线评估过程尽量还原线上环境,线上环境不仅包括线上的数据环境,也包括模型的更新频率等应用环境。
动态离线评估方法
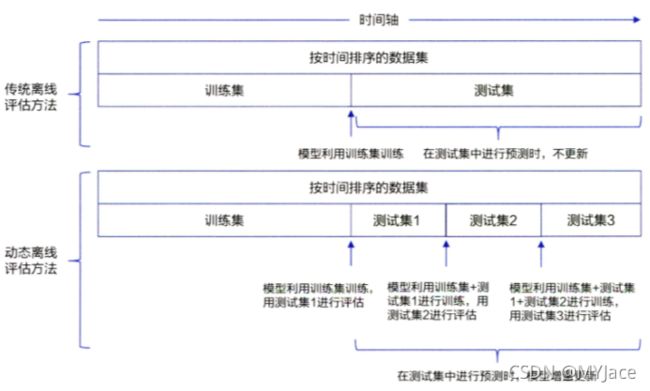
传统离线评估方法的弊端是评估过程是 “静态的” ,即模型不会随着评估的进行而更新。这是和线上环境是完全迥异的情况,因为对于互联网公司来说,长时间不更新模型是不现实的。因此,我们希望能在离线环境下,也模拟出线上的这种 “动态” 环境,以进行评估。
动态离线评估方法首先会根据样本产生时间对测试样本由早到晚进行排序,再用模型根据样本时间依次进行预测。在模型更新的时间点上,模型需要增量学习更新时间点前的测试样本,更新完成后继续进行之后的评估
如果我们提升模型更新频率,让模型每接受一个新样本就更新,那么整个动态评估的过程也变成逐一样本回放的精准线上仿真过程,这就是经典的仿真式离线评估方法 - Replay
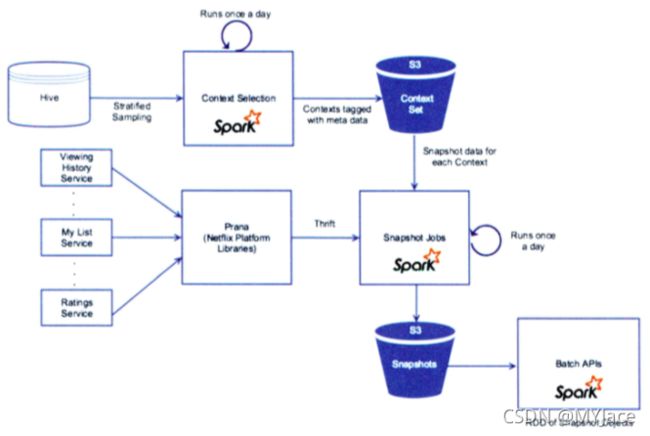
Netflix 的 Replay 评估方法实现
Replay 方法通过重播在线数据流的方法进行离线测试。但这个时候就需要格外注意 “数据穿越” 的问题,即在每个样本产生时,要确保不会包含任何 “未来信息”
比如使用 9.1 到 9.30 的样本数据进行重播,样本中包含一个特征 “历史 CTR”,该特征只会根据历史数据生成。所以 9.20 的样本就只能使用 9.1 到 9.19 的数据生成 “历史 CTR” 这个特征,而绝不能使用 9.20 以后的数据生成这个特征。但是在离线环境下,为了数据使用方便,往往会用 9.1 到 9.30 所有样本数据生成 “历史 CTR” 这个特征,然后所有 9 月的样本数据在 “历史 CTR” 这一特征维度都使用这个计算值。此时如果使用 Replay 必然会有问题,因为 9.30 之前的数据在 “历史CTR” 这个特征上都 “预知未来” 了。
为了进行 Replay 评估,Netflix 构建了 “时光机 (Time Machine)“ 架构:
”时光机“ 以天为单位运行 (Runs once a day)。它的任务主体是 Snapshot Jobs,该任务同时整合当天的各类日志、特征、数据,以形成当天的供模型训练与评估的样本数据。从架构图来看,“时光机” 主要整合了两部分信息:
- 场景信息 (Context):来自 Hive 的相对静态的信息,比如设备 ID,用户信息等
- 系统日志流 (Logs):系统实时产生的日志,包括观看历史、用户推荐列表、用户排名等。这些数据从不同的业务场景中生成,通过 Netflix 提供的 Prana API 对外提供服务
Snapshot Jobs 通过 Prana 获取日志信息,从 S3 获取场景信息 (Context),经过整合处理,存入分布式文件系统 S3 中。此时再进行 Replay 评估,可以直接取用每天的快照 (Snapshots) 作为样本数据即可。
A/B 测试与线上评估指标
但是无论我们如何在线下环境中模拟线上环境,它终归只是模拟,无法达到完全的真实。所以总有一些只能在线上进行评估的指标是无法在线下计算的,另外离线环境下的数据偏置 (bias) 问题依旧难以根除。所以,我们最终还是需要在线上进行评估。
A/B 测试是当前进行线上评估最主流的方法,它的思想非常直白:在利用控制变量法保持单一变量的前提下,将 A, B 两组数据进行对比,得出实验结论。
具体到互联网场景下的算法测试中,可将用户随机分成实验组 (A 组) 和对照组 (B 组)。对实验组的用户使用新模型提供服务,对对照组的用户用旧模型提供服务,比较实验组和对照组在各线上评估指标上的差异
A/B 测试的分组思想
A/B 的分组需要同时保证样本的独立性以及分组的无偏向性。 即同一个用户在测试的全程只能被分到同一个组中,在分组过程中所用的用户 ID 应是一个随机数,这样才能保证组中的样本是无偏向的。
由于业务的复杂性,一般要根据需求进行多组不同类型的 A/B 测试。
比如:在前端进行不同 App 界面的 A/B 测试 , 在业务层进行不同中 间件效率的 A/B 测试,在算法层同时进行推荐场景 1 和推荐场景 2 的 A/B 测试
所以,我们需要慎重决定分层和分流策略,以避免相互干扰。分层和分流机制要始终秉持 2 个原则:
- 层与层之间的流量 “正交“:层与层之间的独立实验的流量是正交的,即实验中每组的流量穿越该层后,都会被再次随机打散,且均匀地分布在下层实验的每个实验组中。比如流量通过前端层之后,再次进行随机划分,分给业务层的 A, B 组来使用
- 同层的流量之间 ”互斥“:如果同层之间进行多组 A/B 测试,那么不同测试之间的流量是不重叠的,同时,一组 A/B 测试中实验组和对照组的流量也是不重叠的。比如在算法层,推荐场景 1 和推荐场景 2 使用的流量 (也就是用户)应当不重复且无偏向性,在每个推荐场景下的 A/B 测试中,实验组和对照组使用的流量 (用户)也要不重复且无偏向性
A/B 测试的线上评估指标
一般来讲, A/B 测试都是模型上线前的最后一道测试,通过 A/B 测试检验的模型将直接服务于线上用户,完成公司的商业目标。 因此, A/B 测试的指标应与线上业务的核心指标保持一致。对于不同业务的推荐模型,评估指标也会有所差异:
可以注意到,A/B 测试的评估指标与业务直接挂钩,而离线评估因为不具备直接计算业务核心指标的条件,因此 退而求其次,选择了偏向于技术评估的模型相关指标。
A/B 测试的问题
A/B 测试一个比较明显的缺陷在于最初对于实验组和对照组的划分可能会对结果造成影响。 比如某网站测试算法时,将众多用户分为两组,但是我们很清楚,重度使用者在总量中并不多,如果这些重度使用者都被分到同一组,那么结论可能就会被极大影响,模型的效果也可能会被掩盖。
快速线上评估方法 - Interleaving
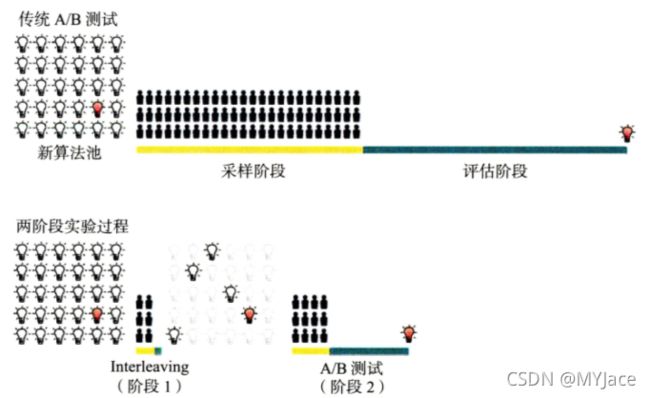
A/B 测试虽然十分有用,但是该评估方法会占用比较多的线上资源同时也会影响到部分用户的体验。为此,微软提出了一种快速线上评估方法 - Interleaving。
Interleaving 实际上为 A/B 测试添加了一个预选阶段,快速筛选候选的算法,从大量的初始 “想法” 中啥选出比较好的算法,再对选出来的这一部分算法进行 A/B 测试以节省资源。
在上图中,用红色灯泡表示最优胜的算法。Interleaving 可以快速缩小最初的候选算法集合,会比 A/B 测试更快地确定最优算法。Interleaving 的一大作用就是解决 A/B 测试中因分组问题导致的不可靠测试结果问题:
比如我们想要测试用户对于 《谍影重重》和《碟中谍》这两部电影的偏向性,此时我们不再简单地将用户分为两组,然后以 “盲测” 的形式为每组只提供某一部影片,过一段时间后根据播放总量来看哪部电影占比更高,这是 A/B 测试会选择的方法。但是 Interleaving 会让用户在实验过程中自己选择去看《谍影重重》还是《碟中谍》,在实验结束后统计每个人观看《谍影重重》和《碟中谍》的比例,然后对每个人的观看比例进行平均,得到整体的观影比例,得出整体的偏向性
该方法的优点在于:
- 抹消了 A/B 测试者本身属性分布不均匀带来的问题
- 通过给予每个人相同的权重,降低了重度消费者对结果的过多影响
这种不区分 A/B 组 , 而是把不同的被测对象同时提供给受试者 , 最后根据受试者喜好得出评估结果的方法就是 Interleaving 方法 。
Interleaving 的实现
现在我们把 Netflix 作为具体的例子来理解 Interleaving。在 A/B 测试中,用户会被分为两组,分别由排序算法 A 和排序算法 B 提供服务。而在 Interleaving 方法中 ,只有一组订阅用户,这些订阅用户会收到通过混合算法 A 和 B 的排名生成的交替排名,也就是说用户会在一行内同时看到算法 A 和算法 B 推荐的结果(用户无法区 分一个物品是由算法 A 推荐的还是由算法 B 推荐的),进而通过计算观看时长等指标来衡量到底是算法 A 的效果好还是算法 B 的效果好。
为了避免来自算法 A 推荐的视频总排在首位,需要让这两个算法以相同的概率交替呈现推荐结果:
我们需要从 “灵敏度” 和 “正确性” 这两个指标来判断 Interleaving 是否比 A/B 测试更优秀
“灵敏度” 比较
所谓的 “灵敏度” 就是 Interleaving 是否能比 A/B 测试使用更少的样本验证出算法 A 和算法 B 的优劣。
上图是 Interleaving 和传统 A/B 测试 “灵敏度” 实验对比曲线图。可以看到,横轴是参与实验的样本数量,纵轴是 p-value。根据曲线能够看到,Interleaving 仅用 103 样本就能判断算法 A 是否比算法 B 更好;而 A/B 测试则要 105 样本才能将 p-value 降低到 5% 以下。这意味着 Interleaving 仅用 A/B 测试 1% 的样本就能确定哪个算法更优胜,无疑大大节省了资源。
Interleaving 指标与 A/B 测试指标的相关性
在得到 Interleaving 比起 A/B 测试 “灵敏度” 更高的结论之后,我们现在需要验证通过 Interleaving 得出的结论的 “正确性”,即其结论是否与 A/B 测试的结论相匹配。
在上面这张图中,每个数据点代表一个推荐模型。可以看到 Interleaving 与 A/B 测试之间的相关性很强,这就验证了在 Interleaving 实验中胜出的算法也极有可能在之后的 A/B 测试中胜出。换言之,Interleaving 得出的结论与 A/B 测试的结论基本相匹配。
*需要注意,Interleaving 实验中展现的仅仅是实验用混合界面,所以需要测试某个算法的真实效果时,仍需要借助 A/B 测试,他在实验的全面性和权威性上有着巨大优势
Interleaving 的优缺点
优点:
- 所使用的样本更少,得出结论的速度更快且结论基本与 A/B 测试一致
缺点:
- Interleaving 方法的实验逻辑和业务逻辑纠缠在一起,因此业务逻辑可能会被干扰,这需要借助更多的辅助性数据标识。因此工程难度较高
- Interleaving 方法只是对 “用户对算法推荐结果偏好程度” 的相对测量 , 不能得出一个算法真实的表现。如果想要算法 A 比算法 B 在某项指标上具体胜出多少之类的细节数据,就需要使用 A/B 测试才能得到
推荐系统的评估体系
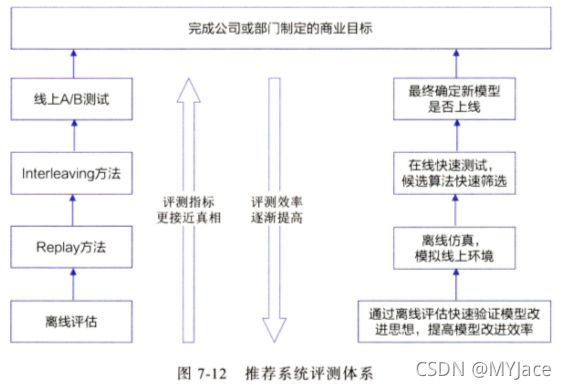
一个成熟的推荐系统评估体系应综合考虑评估效率和正确性,利用较少的资源,快速地筛选出效果更好的模型。对此,我们需要铭记以下几点:
- 线上测试更接近实际的业务情况,为靠近业务目标提供了更好的机会,但是会比较耗费宝贵的线上资源
- 离线测试可以利用近乎无限的离线计算资源,快速得出评估结果,从而快 速实现模型的迭代优化
- Replay 方法能够最大程度地在离线状态下模拟线上测试过程, Interleaving 方法则可以建立快速的线上测试环境
在上面的评测体系示意图中,左侧是一系列评估方法,右侧则是 “金字塔” 一般的模型筛选过程。可以清楚地看到:
- 越靠近底层待筛选的模型越多,需要改进的思想也越多,此时处于完全的离线环境,训练数据量巨大,因此对于训练的 “效率” 更看重
- 越靠近顶层,即离实际部署上线提供服务越近,对于 “正确性” 看得越重(在模型正式上线前,应该以最接近真实产品体验的 A/B 测试做最后的模型评估,产生最具说服力的在线指标之后,才能进行最终的模型上线,完成模型改进的迭代过程)